You can also find all 50 answers here 👉 Devinterview.io - Time Series
A time series is a sequence of data points indexed in time order. It is a fundamental model for many real-world, dynamic phenomena because they provide insights into historical patterns and can be leveraged to make predictions about the future.
Time series data exists in many domains, such as finance, economics, weather monitoring, and signal processing. Its unique properties and characteristics require specialized techniques for effective analysis.
- Temporal Nature: Data points are indexed in time order, often with a regular or irregular time interval between observations.
- Trends: Data can exhibit upward or downward patterns over time, capturing long-term directional movements.
- Seasonality: Certain data distributions are influenced by regular, predictable patterns over shorter time frames, often related to seasons, months, days, or even specific times of day.
- Cyclical Patterns: Some time series data can fluctuate in repeating cycles not precisely aligned with calendar-based seasons or specific timeframes.
- Noise: Random, unpredictable variations are inherent in time series data, making it challenging to discern underlying patterns.
- Time Series Forecasting: Predicting future values based on historical data.
- Anomaly Detection: Identifying abnormal or unexpected data points.
- Data Imputation: Estimating missing values in time series.
- Pattern Recognition: Locating specific shapes or features within the data, such as peaks or troughs.
Autocorrelation refers to a time series' degree of correlation with a lagged version of itself. It provides insight into how the data points are related to each other over time.
- Cross-Correlation correlates two time series to identify patterns or directional causal relationships.
- Partial Autocorrelation helps tease out the direct relationship of lagged observations on the current observation, removing the influence of intermediate time steps.
Time series decomposition breaks down data into its constituent components: trend, seasonality, and random noise or residuals.
- A simple additive model combines the components by adding them together,
- while a multiplicative model multiplies them,
Decomposition aids in understanding the underlying structure of the data.
Data smoothing methods help diminish short-term fluctuations, revealing the broader patterns in the time series:
- Simple Moving Average: Computes averages over fixed-size windows.
- Exponential Moving Average: Gives more weight to recent observations.
- Kernel Smoothing: Uses weighted averages with kernels or probability density functions.
A time series is said to be stationary if its statistical properties such as mean, variance, and autocorrelation remain constant over time. Many time series modeling techniques, like ARIMA, assume stationarity for effective application.
While achieving strict stationarity might be challenging, transformations like differencing or detrending the data are often employed to make the data stationary or suit the model's requirements.
Stationarity refers to a time series where the statistical properties such as mean, variance, and covariance do not change over time.
A stationary time series is easier to model and often forms the foundation for many time series and forecasting techniques.
-
Meaningful Averages: A consistent mean provides better insights over the dataset's entire range of values.
-
Predictability: Consistent variance enables improved forecasting accuracy.
-
Valid Assumptions: Many statistical tests and methods assume stationarity.
-
Simplicity: It simplifies the model by keeping parameters constant over time.
-
Insight into Data: Trends and cycles are more apparent in non-stationary data after applying techniques like differencing.
- Differencing: A simple way to stabilize the mean and remove trends.
- Log Transformations: Particularly useful when the variance grows exponentially.
- Seasonal Adjustments: Filtering out periodic patterns.
-
Data Segmentation: Focusing on specific time intervals for analysis.
-
Trend Removal: Often done using linear regression or polynomial fits.
Time Series and Cross-Sectional Data are distinct types of datasets, each with unique characteristics, challenges, and applications.
- Temporal Order: Observations are recorded in a sequence over time.
- Temporal Granularity: Time periods between observations can vary.
- Types of Variables: Typically contains a mix of dependent and independent variables, with one variable dedicated to time.
- Examples: Stock Prices, Weather Data, Population Growth over Years.
- Absence of Temporal Order: Data points are observational at a single point in time; they don't have a time sequence.
- Constant Time Frame: All observations are made at a single, specific time or time period.
- Types of Variables: Usually includes independent variables and a response (dependent) variable.
- Examples: Survey Data, Demographic Information, and Financial Reports for a Single Time Point.
- Methods: Time series data employs techniques such as ARIMA (AutoRegressive Integrated Moving Average), Exponential Smoothing, and other domain-specific forecasting models.
- Challenges Addressed: Trends, seasonality, and noise are significant areas of focus.
- Methods: This data often calls upon classic statistical approaches like linear and logistic regression for predictive modeling.
- Challenges Addressed: Relationships between independent and dependent variables are of primary importance.
- Lag Features: Incorporating lagged (historic) values significantly impacts the model's predictive capabilities.
- Temporal-Sensitive Validation: Techniques like "rolling-window" validation are essential to accurately assess a time series model.
- Persistence Models: Simple models like the moving average can often serve as strong benchmarks.
- Randomness Management: To maintain randomness in data, techniques like cross-validation and bootstrapping are used.
Here is the Python code:
import pandas as pd
# Creating example time series data
time_series_df = pd.DataFrame({
'date': pd.date_range(start='2023-01-01', periods=10),
'sales': [50, 67, 35, 80, 65, 66, 70, 55, 72, 90]
})
# Creating example cross-sectional data
cross_sectional_df = pd.DataFrame({
'category': ['A', 'B', 'C', 'B', 'A'],
'value': [10, 20, 15, 30, 25]
})
print(time_series_df.head())
print(cross_sectional_df.head())Seasonality in time series refers to data patterns that repeat at regular intervals. For instance, sales might peak around holidays or promotions each year.
-
Visual Inspection: Plotting your time series data can help identify distinct patterns that repeat at specific intervals.
-
Autocorrelation Analysis: The autocorrelation function (ACF) is a powerful tool for identifying repeated patterns in the data. Peaks or cycles in the ACF indicate potential seasonality.
-
Subseries Plot: Breaking down your time series into smaller, segmented series based on the seasonal period allows for an easier visual identification of seasonality patterns.
-
Seasonal Decomposition of Time Series: This method uses various techniques, such as moving averages, to separate time series data into its primary components: trend, seasonality, and irregularity.
-
Statistical Tests: Methods like the Augmented Dickey-Fuller (ADF) and Kwiatkowski-Phillips-Schmidt-Shin (KPSS) tests can provide a statistical basis for confirming seasonality.
-
Fourier Analysis: This mathematical approach decomposes a time series into its fundamental frequency components. If significant periodic components are found, it indicates seasonality.
-
Extrapolation Techniques: Forecasting future data points and comparing actual observations against these forecasts can reveal any recurring patterns or cycles, thereby indicating seasonality.
-
Spectral Analysis: This method characterizes periodicities within a time series as they're represented in the frequency domain. The primary tool for spectral analysis is the periodogram, a graphical representation of the power spectral density of a time series. Any "peaks" in the periodogram can indicate periodic behavior of that corresponding frequency.
-
Machine Learning Algorithms: Models like Support Vector Machines (SVMs) and Neural Networks can capture seasonality in training data and make predictions about it in the future.
-
Domain-Specific Knowledge: Understanding of the dataset and the factors that could impact it are also crucial. For example, in Sales data, knowledge about sales cycles can help deduce the seasonality.
Here is the Python code:
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
# Load a dataset
data = sm.datasets.co2.load_pandas().data
# Visual Inspection
plt.plot(data)
plt.xlabel('Year')
plt.ylabel('CO2 Levels')
plt.title('CO2 Levels Over Time')
plt.show()
# Autocorrelation Analysis
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(data)
plt.xlabel('Lag')
plt.ylabel('Autocorrelation')
plt.title('Autocorrelation of CO2 Levels')
plt.show()
# Seasonal Decomposition
decomposition = sm.tsa.seasonal_decompose(data, model='multiplicative', period=12)
decomposition.plot()
plt.show()
# Statistical Tests
from statsmodels.tsa.stattools import adfuller, kpss
ad_test = adfuller(data)
kpss_test = kpss(data)
print(f'ADF p-value: {ad_test[1]}, KPSS p-value: {kpss_test[1]}')
# Domain-Specific Knowledge
# Some datasets may exhibit seasonality based on known external factors, such as weather or holidays. Awareness of these factors can reveal seasonality.In time series analysis, a trend refers to a long-term movement observed in the data that reflects its overall direction. This could mean an increase or decrease over time.
-
Deterministic Trend: The data exhibits consistent growth or decline over time, often seen in straight or curved lines.
-
Stochastic Trend: The trend deviates randomly, making it challenging to predict.
Removing the trend is a fundamental step in time series analysis. De-trending can be accomplished via:
-
First-Differencing: Subtract the previous value from each observation.
-
Log Transformation: Useful for data showing exponential growth.
-
Moving Average: Removes short-term fluctuations to focus on trend.
-
Seasonal Adjustment: Removes regular, recurring patterns, often seen in cyclical data.
Here is the Python code:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# Generate Artificial Data
np.random.seed(0)
dates = pd.date_range('20210101', periods=100)
data = np.cumsum(np.random.randn(100))
# Create Time Series
ts = pd.Series(data, index=dates)
# Plot Data
plt.figure(figsize=(10, 6))
plt.plot(ts, label='Original Data')
# Add Trend Line
ts.rolling(window=10).mean().plot(color='r', linestyle='--', label='Trend Line (Moving Average)')
plt.legend()
plt.show()In the context of time series forecasting, it is important to understand the nature and statistical properties of the data. Two common types, often used as benchmark models, are White Noise and Random Walk.
- White noise represents a random series with each observation being independent and identically distributed (i.i.d).
- Mathematically, it is a sequence of uncorrelated random variables
$x_t$ , each with the same mean$\mu$ and standard deviation$\sigma$ . - The lack of any trend or pattern in white noise makes it an ideal baseline for evaluating forecasting techniques.
- A random walk, unlike white noise, is not independent. Each observation is the sum of the previous observation and a random component.
- The simplest form, known as a "non-drifting" or "standard" random walk, can be written as:
- Here,
$\varepsilon_t$ is the random noise or innovation term.
- Dependence Structure: White noise has no inherent dependencies, whereas a random walk is dependent on prior observations.
- Trend: White noise lacks any trend, while a random walk can have a drift (constant trend) or a unit root (trend correlated with time).
- Stationarity: White noise is stationarity but a random walk is non-stationary. Its statistical properties change over time, making it more challenging for forecasting.
Here is the Python code:
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
# Generate white noise and random walk
white_noise = np.random.randn(1000)
random_walk = np.cumsum(white_noise)
# Plot the series
plt.figure(figsize=(10, 4))
plt.plot(white_noise, label='White Noise')
plt.plot(random_walk, label='Random Walk')
plt.legend()
plt.show()Autocorrelation measures how a time series is correlated with delayed versions of itself. It's a fundamental concept in time series analysis as it helps to assess predictability and pattern persistence.
The AutoCorrelation Function (ACF) is a statistical method used to quantify autocorrelation for a range of lags. An ACF plot provides insights into the correlation structure of a time series across different time points.
The ACF at lag
Here,
The ACF provides numerical values that range between -1 and 1, where:
- A value of 1 indicates perfect positive autocorrelation.
- A value of -1 indicates perfect negative autocorrelation.
- A value of 0 indicates no autocorrelation.
Here is the Python code:
import pandas as pd
from statsmodels.graphics.tsaplots import plot_acf
import matplotlib.pyplot as plt
# Load data
data = pd.read_csv('your_data.csv', parse_dates=['date'], index_col='date')
# Create ACF plot
plot_acf(data, lags=20)
plt.show()Differencing, a fundamental concept in time series analysis, allows for the identification, understanding, and resolution of trends and seasonality.
Time series data often exhibits patterns such as trends and seasonality, both of which can preclude accurate modeling and forecasting. Common trends include an overall increase or decrease in the data points over time. Seasonality implies a periodic pattern that repeats at fixed intervals.
By using differencing, one transforms the time series data into a format that is more suitable for analysis and modeling. Specifically, this method serves the following purposes:
-
Detrending: The removal of time-variant trends helps in focusing on the residual pattern in the data.
-
De-Seasonalization: Accounting for periodic fluctuations allows for a more clear understanding of the data's behavior.
-
Data Stabilization: By reducing or removing trends and/or seasonality, the time series data can be made approximately stationary. Stationary data has stable mean, variance, and covariance properties across different time periods.
-
Noise Filtering: The process can help in isolating the underlying pattern or trend in the data by minimizing the impact of noise.
-
First-Order Differencing:
$\Delta y_t = y_t - y_{t-1}$ This is often utilized when dealing with data that exhibits a constant change (i.e., first-order trend) and might require multiple iterations for adequate detrending.
-
Seasonal Differencing:
$\Delta_s y_t = y_t - y_{t-s}$ Specifically tailored for data that shows seasonality. The
sin the equation represents the seasonal period. -
Mixed Differencing: This technique combines both first-order and seasonal differencing, which is especially useful for data showing both trends and seasonality.
Here is the Python code:
import pandas as pd
# Generate some example data
data = pd.Series([3, 5, 8, 11, 12, 15, 18, 20, 24, 27, 30])
# Perform first-order differencing
first_order_diff = data.diff()
# Print the results
print(first_order_diff)Here is the Python code:
import pandas as pd
# Generate some example data
monthly_data = pd.Series([120, 125, 140, 130, 150, 160, 170, 180, 200, 190, 210, 220, 230, 240])
# Perform seasonal differencing (using 12 months as the seasonal period)
seasonal_diff = monthly_data.diff(12)
# Print the results
print(seasonal_diff)The Autoregressive (AR) model is a popular approach in time series analysis. It refers to a time series forecast technique wherein the present value is made a function of its preceding values modified by a potential random shock. Essentially, it models the current value as a linear combination of past data.
The generic AR model equation for a univariate time series is:
Where:
-
$X_t$ is the observation at time$t$ -
$c$ is a constant -
$\phi_1, \phi_2, \ldots, \phi_p$ are the p lag coefficients -
$p$ is the order of the model -
$\varepsilon_t$ is the white noise term at time$t$
The model involves several key components, such as the order, coefficients, and residual term.
- Data Exploration: AR models are fundamental in time series data exploration and analysis.
- Forecasting: These models can make accurate short-term predictions, especially when the history is the best indicator of the future.
-
Error Tracking: The white noise term,
$\varepsilon_t$ , accounts for unexplained variation and helps in understanding forecasting errors.
Choosing the right order of the AR model is essential for a balanced trade-off between complexity and accuracy. Key selection methods include:
- Visual Inspection: Plotting the autocorrelation function (ACF) and partial autocorrelation function (PACF) can provide an initial estimate of the order.
- Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC): These information-based criteria assess model fit, favoring parsimony.
The coefficients
Here is the Python code:
import numpy as np
import statsmodels.api as sm
from statsmodels.tsa.ar_model import AutoReg
from statsmodels.tsa.arima_process import ArmaProcess
import matplotlib.pyplot as plt
# Generate AR(1) process
np.random.seed(42)
ar1 = np.array([1, -0.5])
ma = np.array([1])
ar1_process = ArmaProcess(ar1, ma)
ar1_data = ar1_process.generate_sample(nsample=100)
plt.plot(ar1_data)
plt.title('AR(1) Process')
plt.show()
# Fit an AR model using AutoReg
ar_model = AutoReg(ar1_data, lags=1)
ar_model_fit = ar_model.fit()
# Print model summary
print(ar_model_fit.summary())The Moving Average model (MA) is a core tool for time series analysis. It serves as a building block for more advanced methods like ARMA and ARIMA.
The MA model estimates a time series' future value as a linear combination of past error terms.
Its core components include:
-
Error Term (White Noise): Represents random fluctuations in the time series.
-
Coefficients: Determine the influence of the previous error terms on the present value.
$$Y_t = \mu + \varepsilon_t + \theta_1\varepsilon_{t-1} + \theta_2\varepsilon_{t-2} + \ldots + \theta_q\varepsilon_{t-q}$$
Here,
The backbone of the graphical representation of the MA process is the auto-covariance function. This function offers a detailed view of how data points in time series are related to one another.
The auto-covariance function, denoted as
- When
$k = 0$ ,$\gamma(0)$ is the variance of the time series, denoted by$\sigma^2$ . - For any other
$k$ , if$k = i$ , where$i$ is a positive integer, then$\gamma(k)$ indicates the covariance between the series at time$t$ and the series at time$t - k$ . - If
$k \neq i$ , then$\gamma(k)$ is$0$ , suggesting no covariance between these points.
In mathematical notation:
where
To illustrate the concept, we'll simulate a Moving Average (MA) process and visualize it alongside its auto-covariance function.
Here is the Python code:
import numpy as np
import matplotlib.pyplot as plt
# Define the parameters
n = 1000
mean = 0
std_dev = 1
q = 3 # Order of the MA model
# Generate the white noise error terms
epsilon = np.random.normal(loc=mean, scale=std_dev, size=n+q) # Include some extra to allow for "burn-in"
# Generate the MA process
ma_process = mean + epsilon[q:] + 0.6*epsilon[q-1:-1] - 0.5*epsilon[q-2:-2]
# Visualize the MA process
plt.figure(figsize=(12, 7))
plt.subplot(2, 1, 1)
plt.plot(ma_process)
plt.title('Simulated Moving Average Process')
# Calculate the auto-covariance function
acf_values = [np.cov(ma_process[:-k], ma_process[k:])[0, 1] for k in range(n)]
# Visualize the auto-covariance function
plt.subplot(2, 1, 2)
plt.stem(acf_values)
plt.title('Auto-Covariance Function')
plt.xlabel('Lag (k)')
plt.ylabel('Auto-Covariance')
plt.show()The ARMA (AutoRegressive Moving Average) model merges autoregressive and moving average techniques for improved time series forecasting.
The AR component uses past observations
where:
-
$\phi_1, \phi_2, \ldots$ are the AR coefficients. -
$c$ is the mean of the time series. -
$\epsilon_t$ is the error term.
The MA part models the relationship between the error term at the current time and those at previous times
where:
-
$\theta_1, \theta_2, \ldots$ are the MA coefficients. -
$\mu$ is the mean of the error term.
Here is the Python code:
# Import necessary libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.arima_process import ArmaProcess
# Simulate ARMA process
np.random.seed(0)
ar_params = np.array([0.8, -0.6]) # AR parameters
ma_params = np.array([1.5, 0.7]) # MA parameters
ARMA_process = ArmaProcess(ar_params, ma_params)
samples = ARMA_process.generate_sample(nsample=100)
# Plot the time series
plt.plot(samples)
plt.xlabel('Time')
plt.ylabel('Value')
plt.title('Simulated ARMA(2,2) Process')
plt.show()ARMA (Auto-Regressive Moving Average) is undoubtedly a useful modeling technique, but it's limited in its application to strictly stationary time series data.
Time series data that exhibits varying statistical properties over time, including mean and variance, are labeled as non-stationary.
While transformations like differencing can often uncover stationarity, this step might not suffice for complete stationarity. This discrepancy prompted the development of the ARIMA model to account for such data.
ARIMA (Auto-Regressive Integrated Moving Average) takes non-stationarity in its stride through the process of integration. This method differs from the standalone differencing technique and allows for a diverse set of non-stationary time series data to be modeled effectively.
Integration, denoted by the parameter
Full-fledged ARIMA thus comprises three constituent elements: AR for auto-regression, I for integration, and MA for the moving average model. These elements come together to embody a potent, versatile modeling technique, capable of accurately representing a gamut of complex time series datasets.
13. What is the role of the ACF (autocorrelation function) and PACF (partial autocorrelation function) in time series analysis?
AutoCorrelation Function (ACF) and Partial AutoCorrelation Function (PACF) are types of statistical functions used to understand and model time series data.
The ACF is a measure of how a data series is correlated with itself at different time lags.
- At lag 0, ACF is always 1.
- At lag 1, ACF indicates the correlation between adjacent points.
- At lag 2, ACF captures the correlation between two points one time unit apart and so on.
PACF measures the correlation between two data points while accounting for the influence of other data points in between. Here's how it is calculated:
- The correlation at lag 1 (between points 1 and 2) is the same in ACF and PACF as there's only one data point in between.
- For lag 2 (between points 1 and 3), the correlation considers only point 2, effectively removing the influence of point 2 in calculating the correlation between points 1 and 3.
PACF essentially "cleans" the relationship between data points from the influence of intervening points.
By plotting ACF and PACF, you can glean crucial insights about your time series data, such as whether it's stationary or displays certain patterns:
-
Exponential Decay: If the ACF exhibits rapid decay after a few lags, the time series might display an exponential decay pattern.
-
Damped Sine Wave: A pattern of alternating positive and negative correlations in the ACF, often seen in seasonal time series.
-
Sharp Cut-offs: An ACF that stops sharply after a certain number of lags might indicate a series that follows a moving average process.
Lag selection in models like ARMA (AutoRegressive–Moving-Average) and ARIMA (AutoRegressive-Integrated-Moving-Average) is a crucial step in understanding time series data and making accurate predictions.
-
Auto-Relationships: AR models capture the relationship between an observation and a number of lagged observations. The number of lags is determined by the parameter p.
-
Auto-Relationships After Differencing: When differencing is applied to make the series stationary, ARMA models- essentially working on the now stationary series- can model the relationships between the differenced series and lagged values of the original series for both AR and MA. Differencing introduces new lags, hence p can differ from p- the 'pre-differencing' lag count.
-
Memory: Both AR and MA components can be affected by historical values to a certain extent, known as the memory length or recurrent lag. This lag is one of the most important time series diagnostics.
- Visual Analysis: Plot ACF and PACF to identify the order of the process.
- Information Criterion: AIC and BIC help quantitatively compare models with different lag lengths. Lower values indicate a better fit.
- Out-of-sample Prediction: Using a part of the data for model selection and the rest for testing its forecasting ability.
- Cross-Validation: Split the data into multiple segments. Train the model on some segments and validate on others to assess predictive accuracy.
- Use of Software: Dedicated software often has built-in algorithms to determine the best lags.
Here is the Python code:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
# Simulate AR(2) process
np.random.seed(100)
n = 100
ar_params = np.array([1.2, -0.4])
ma_params = np.array([1])
disturbance = np.random.normal(0, 1, n)
y_values = sm.tsa.ArmaProcess(ar_params, ma_params).generate_sample(disturbance)
# Define ACF and PACF plots
fig, ax = plt.subplots(1,2,figsize=(10,5))
sm.graphics.tsa.plot_acf(y_values, lags=20, ax=ax[0])
sm.graphics.tsa.plot_pacf(y_values, lags=20, ax=ax[1])
ax[0].set_title('ACF')
ax[1].set_title('PACF')
plt.show()In a SARIMA model, non-stationarity is addressed by differencing, while seasonality is managed through seasonal differencing (
The general formula for managing seasonality, especially in the context of the $k$th seasonal lag or difference period, can be written as:
Here,
The seasonal AR and MA terms are the 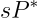
Here is the Python code:
import pandas as pd
# Generate Sample Data
data_range = pd.date_range(start='1900-01-01', end='1900-07-01', freq='MS')
data = [i**2 for i in range(7)]
ts = pd.Series(data=data, index=data_range)
# Seasonal Differencing
D = 1
s = 12
seasonal_difference = (ts - ts.shift(s))[D:]
# Plot Result
import matplotlib.pyplot as plt
plt.plot(seasonal_difference)
plt.show()Explore all 50 answers here 👉 Devinterview.io - Time Series