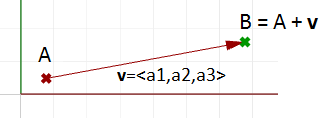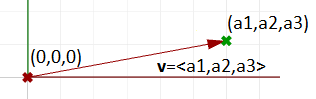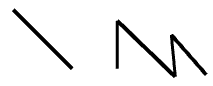译者序:
时间来到了2024年这个节点,《Essential Mathematics for Computational Design》这本书已然出版到了第四版,译者在Rhino使用过程中深感基础数学知识的重要性。又见第四版相较第二版有了较多案例和行文的变化,故起重新翻译之心。
本译本以Rhino开发者网站上的版本为主,参考了第四版PDF和第二版中文翻译。
本书版权显然仍归属原作者及McNeel公司所有。如有错漏及翻译问题,请联系译者。
本书基本为译者使用markdown手动翻译、感谢作者***Rajaa Issa***的帮助,我向作者询问了本书的一些问题,得到很多帮助和反馈。
翻译过程中发现了原书版本的一些排版问题,这些问题已被原作者修复。
pdf输出使用Typora主题typora-latex-theme。
ArchiBC: Archi-BC@outlook.com 中建五局设计技术科研院
向设计专业人员介绍有效开发计算3D模型的基础数学概念。
《计算设计的基础数学》向设计专业人员介绍了有效开发 3D 建模和计算机图形学计算方法所必需的基础数学概念。这并不是一个完整而全面的资源,而是对基本和最常用概念的概述。该材料面向高中以上几乎没有数学背景的设计师。所有概念都使用Grasshopper可视化解释。有关Grasshopper®(GH)和Rhinoceros®(Rhino)的具体信息,请参阅如下链接,https://discourse.mcneel.com/c/grasshopper/2和https://www.rhino3d.com/
译者注:原文有关GH引用的链接为https://www.grasshopper3d.com/,但不幸的是该网站基本上已经停止运营,故链接到了官方GH论坛。中文读者也可通过访问https://forum.rhino3d.com.cn/来获取中文的Rhino和GH资料并讨论问题。
所有内容分为三章。第一章讨论向量数学,包括向量的表示,向量的运算以及直线和平面方程。第二章回顾了矩阵运算和转换,第三章包含了参数曲线,特别是NURBS曲线以及连续性和曲率的概念,另外还简单回顾了NURBS曲线和曲面。
我要感谢Robert McNeel & Associates的Dale Lear博士出色而彻底的技术审查。他的宝贵意见对本版的制作起到了重要作用。我还要感谢Robert McNeel & Associates的Margaret Becker女士对技术写作和格式的审查。
Robert McNeel & Associates
版权信息:
Essential Mathematics for Computational Design, Fourth Edition, by Robert McNeel & Associates, 2019 is licensed under a Creative Commons Attribution-Share Alike 3.0 United States License.
目录
[TOC]
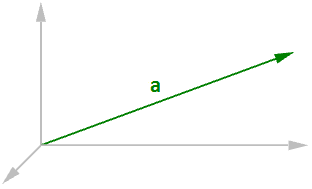
向量表示一个有长度和方向的量,例如速度和力。三维坐标系下向量用三个有序实数表示,如下所示:
在本文档中,带箭头的小写粗体字母表示向量,向量分量用尖括号括起。大写字母表示点,点的坐标用圆括号括起。
使用坐标系和任何一个坐标系内的起始点,我们可以通过线段表示或者可视化这些向量。用箭头表示矢量方向。
例如,如果我们有一个向量在三维坐标系中平行于x轴,并且长度是5个单位我们可以写出这个向量:
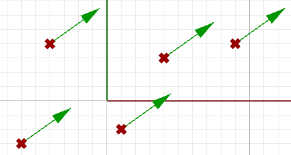
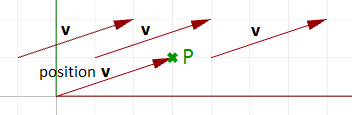
为了表示这个向量,我们需要一个坐标系内的起始点。例如,下图中的所有箭头都是一个相同向量的等价表示,尽管它们位于不同的位置。
图1:三维坐标系中的向量表示Note
给定一个3D向量$\mathbf{\vec{v}}=<a_1,a_2,a_3>$,向量的分量$a_1,a_2,a_3$是实数,所有的从点$A(x,y,z)$到点$B(x+a_1,y+a_2,z+a_3)$的线段都是向量$\mathbf{\vec{v}}$的等价表示。
因此,我们如何定义代表给定向量的线段的结束点呢,我们先定义起始点$A$,令
和一个向量:
那么结束点$B$对应的向量应该通过起始点和向量$\vec{v}$的分量加和得到。
一种特殊的向量表示方法使用 origin point(0,0,0) 作为向量的起始点,那么位置向量$\mathbf{\vec{v}}=<a_1,a_2,a_3>$能够被原点和结束点$B$构成的线段表示。由此得到:
Note
一个给定向量的位置向量$\mathbf{\vec{v}}=<a_1,a_2,a_3>$能被从原点到点$(a_1,a_2,a_3)$的特殊线段表示。
不要混淆向量和点,他们是非常不同的概念,正如我们之前所说,向量表示具有长度和方向的量,但点表示位置。例如,北方是一个向量,北极是一个位置(点)。如果我们有一个向量和一个点具有相同的分量,例如:
我们可以绘制如下向量和点:
图4:向量定义方向和长度。点定义位置正如前面所说,向量有长度,我们使用$|\mathbf{a}|$来表示给定向量$\mathbf{\vec{a}}$的长度,例如:
一般来说,向量$\vec{a}=<a_1,a_2,a_3>$的长度的计算如下:
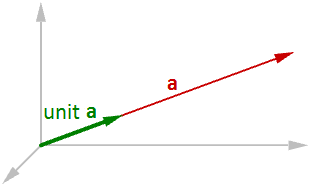
单位向量是长度等于一个单位的向量,单位向量通常用于比较向量的方向。
Note
单位向量是长度等于一个单位的向量
要计算一个单位向量,需要找到需要计算向量的长度,并且将向量的分量除以向量长度。例如:
一般的:
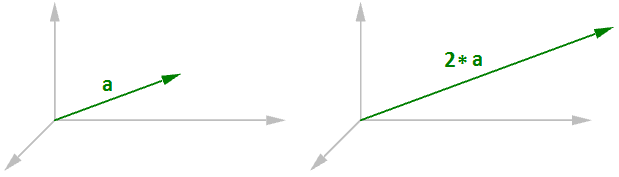
向量的标量运算就是一个一个向量乘以一个实数。例如:
一般的:给定向量$\mathbf{\vec{a}}=<a_1,a_2,a_3>$和一个实数$t$
$$t*\mathbf{\vec{a}}=<ta_1,ta_2,t*a_3>$$
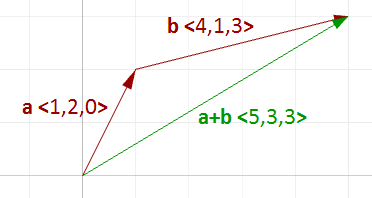
向量加法是两个向量之间的运算并且得到第三个向量,我们通过加和向量的分量来实现向量相加。
Note
向量加法通过分量相加实现
例如,我们有两个向量:
一般来说,两个向量相加的运算如下:
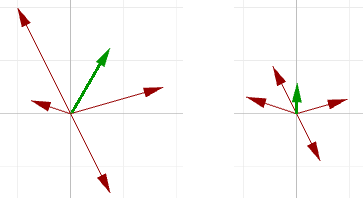
向量相加对于找到两个或者更多向量的平均方向非常有用。在这种情况下,我们通常使用相同长度的向量。下面是一个例子展示了使用相同长度向量和不同长度向量加和的区别。
图9:对不同长度向量求和(左)对相同长度向量求和(右)来获得平均方向向量减法是两个向量的运算并且得到第三个向量,我们通过向量分量相减来实现向量的减法。例如,如果我们有两个向量$\mathbf{\vec{a}}$和$\mathbf{\vec{b}}$,并且我们令$\mathbf{\vec{a}}$减去$\mathbf{\vec{b}}$,那么:
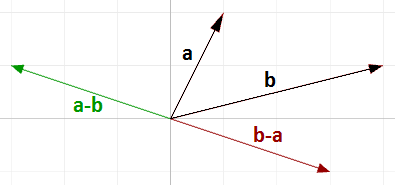
如果我们令$\mathbf{\vec{b}}$减去$\mathbf{\vec{a}}$,我们会得到不同的结果:
注意向量$\mathbf{\vec{b}}-\mathbf{\vec{a}}$和$\mathbf{\vec{a}}-\mathbf{\vec{b}}$长度相同但是方向相反。
图10:向量减法一般来说,如果我们有两个向量$\mathbf{\vec{a}}$和$\mathbf{\vec{b}}$,那么$\mathbf{\vec{a}}-\mathbf{\vec{b}}$向量的计算如下:
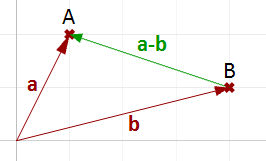
向量减法通常用于找到两个点之间的向量,所以如果我们需要找到一个从位置向量$\mathbf{\vec{b}}$结束点到位置向量$\mathbf{\vec{a}}$结束点的向量,我们就会使用向量减法令$\mathbf{\vec{a}}-\mathbf{\vec{b}}$,如图11所示:
图11:使用向量减法找到两点之间的向量这里有八个向量的基本特性,令$\mathbf{\vec{a}}$,$\mathbf{\vec{b}}$,$\mathbf{\vec{c}}$为向量,$s$,$t$为实数,我们有这样几条性质:
$$st\mathbf{\vec{a}}=s*(t*\mathbf{\vec{a}})$$
$$(s+t)\mathbf{\vec{a}}=s\mathbf{\vec{a}}+t*\mathbf{\vec{a}}$$
向量点积是一个两个向量得到一个实数的运算。例如,如果我们有两个向量$\mathbf{\vec{a}}$和$\mathbf{\vec{b}}$
那么,点积是向量各分量乘积的和:
$$\mathbf{\vec{a}}\cdot\mathbf{\vec{b}}=15+26+3*7$$
通常来说,给两个向量$\mathbf{\vec{a}}$和$\mathbf{\vec{b}}$:
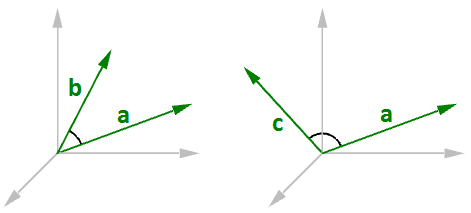
当我们做点积运算时,两个向量有相同的方向时我们能得到一个正实数。两个向量之间的点积为负意味着两个向量有相反的方向。
图12:当两个向量同方向时,结果是正点积(左),当两个向量不同方向时,结果是负点积(右)当计算两个单位向量的点积时,结果在-1到1的闭区间上。例如:
另外向量和向量自身的点积是向量长度的平方。例如:
计算$\mathbf{\vec{a}}$的长度的平方:
两个向量的点积和他们之间的夹角有关。
Note
两个非零单位向量的点积等于两向量夹角点余弦值
一般的:
$$\mathbf{\vec{a}}\cdot\mathbf{\vec{b}}=|\mathbf{\vec{a}}||\mathbf{\vec{b}}|\cos\theta$$
或者表示为:
在这里:
如果两个向量均为单位向量,我们把公式简化为:
因为90度角的余弦值是0所以我们有结论:
Note
当且仅当$\mathbf{\vec{a}}\cdot\mathbf{\vec{b}}=0$时,$\mathbf{\vec{a}}$垂直于$\mathbf{\vec{b}}$。
例如我们计算两个正交向量——x轴单位向量和y轴单位向量的点积,结果为0.
$$\mathbf{\vec{x}}\cdot\mathbf{\vec{y}}=10+01+0*0$$
点积和一个向量到另一个向量的投影长度也有关系。例如:
$$\mathbf{\vec{a}}\cdot unit;\mathbf{\vec{b}}=51+20+0*0=5$$
等于$\mathbf{\vec{a}}$到$\mathbf{\vec{b}}$的投影长度
图13:一个向量的投影长度是一个向量和另一个向量的单位向量的点积一般来说,给定一个向量$\mathbf{\vec{a}}$和一个非零向量$\mathbf{\vec{b}}$,我们可以计算投影长度$pL$通过计算向量$\mathbf{\vec{a}}$和向量$\mathbf{\vec{b}}$的单位向量的点积。
如果$\mathbf{\vec{a}}$、$\mathbf{\vec{b}}$、$\mathbf{\vec{c}}$是向量,$s$是实数,我们有如下性质:
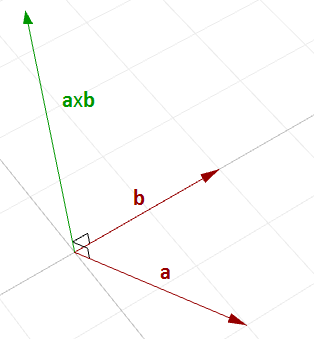
叉积是两个向量得到第三个垂直于两向量的向量的运算。
图14:计算两个向量的叉积例如,如果有两个在XY平面上的向量,则他们的叉积是一个垂直于XY平面的向量,方向为正或负的Z轴方向。
$$\mathbf{\vec{a}}\times\mathbf{\vec{b}}=<(10-02),(01-30),(32-01)>$$
Note
向量$\mathbf{\vec{a}}\times\mathbf{\vec{b}}$垂直于$\mathbf{\vec{a}}$和$\mathbf{\vec{b}}$
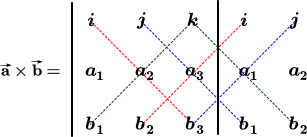
你可能永远不需要手工计算两个向量的叉积,但如果你对如何计算有兴趣,请读下一节,否则可以跳过,叉积是用行列式进行定义的。以下是如何使用标准基向量进行行列式的简单示例。
两个向量$\mathbf{\vec{a}}=<a_1,a_2,a_3>$和$\mathbf{\vec{b}}=<b_1,b_2,b_3>$的叉积使用上图计算如下:
译者注:这个解释过于抽象,建议观看3Blue1Brown的线性代数视频加以理解。或者看看英文版本附带的视频。
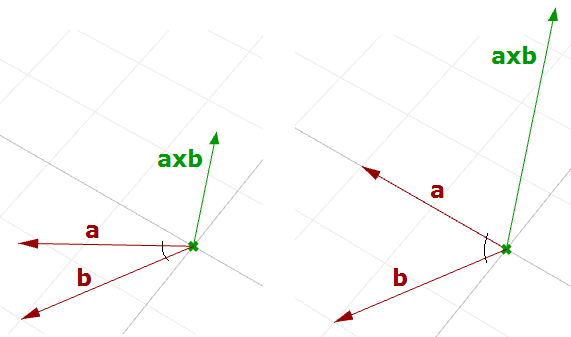
两个向量之间的夹角和向量叉积的模有关。角度越小(正弦值越小),叉积的模越短。在向量叉积运算中,运算次序很重要,例如:
在犀牛的右手系中,$\mathbf{\vec{a}}\times\mathbf{\vec{b}}$的方向由右手定则给出(其中$\mathbf{\vec{a}}$是食指,$\mathbf{\vec{b}}$是中指,$\mathbf{\vec{a}}\times\mathbf{\vec{b}}$是拇指)
一般来说对任意的两个向量$\mathbf{\vec{a}}$和$\mathbf{\vec{b}}$
其中:
如果$\mathbf{\vec{a}}$和$\mathbf{\vec{b}}$是单位向量,那么我们可以说,两向量叉积的模等于向量夹角的正弦。也就是:
两个向量叉积帮我们判断两个向量是否平行,当平行时叉积为零向量。
Note
向量$\mathbf{\vec{a}}$和$\mathbf{\vec{b}}$平行,当且仅当$\mathbf{\vec{a}}\times\mathbf{\vec{b}}=0$。
如果$\mathbf{\vec{a}},\mathbf{\vec{b}}和\mathbf{\vec{c}}$是向量,$s$是一个实数,我们有如下性质:
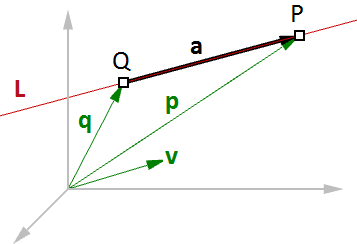
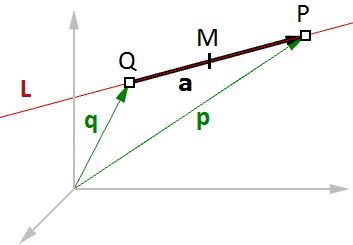
直线的矢量方程适用与三维建模应用和计算机图形学。
图16:直线的矢量方程例如,如果我们知道一条直线的方向和直线上的一个点,那么我们可以使用向量的方法,找到这条直线上的任意一点。如下所示:
我们知道:
由(1)和(2)可知:
由此,我们可以将(3)式改写为:
也就是:
等价于:
Note
给定直线上一点$Q$和方向$\vec{v}$,直线上任意一点$P$都可以用方程$P=Q+t*\vec{v}$计算,$t$是参数。
另一个常用的例子是找两点的中点,下面显示了如何使用直线的向量方程找到中点:
由向量减法可知:
由向量的直线方程可知:
既然我们需要找到中点,那么令:
因此我们得到:
一般的,通过使用该方程将t跟改为0和1之间的值,可以找到Q和P之间任意点:
Note
给定两个点$P$和$Q$,两点之间任意一点$M$都能使用方程$M=Q+t*(P-Q)$计算,其中$t$在0和1之间。
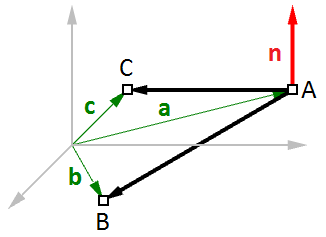
定义平面的一种方法是,通过一个点和一个垂直于平面的向量。这个向量被称作平面的法向向量。法线方向指向平面正上方。
例如当我们知道平面三个不共线的点时,该如何计算平面的法向。
见图18:令:
并且:
我们可以找到法向向量$\mathbf{\vec{n}}$:
图18:向量和平面译者注:a,b,c任意两两组合相减做叉积都可以找到法向
我们还能利用向量点积推导平面的隐式方程:
如果:
带入上式可得:
解这个点积可以得到平面的隐式方程:
我们在本章学习到的所有概念都可以用于解决建模时常见的几何问题,以下时使用本章学习到的概念使用犀牛和Grasshopper的具体教程。
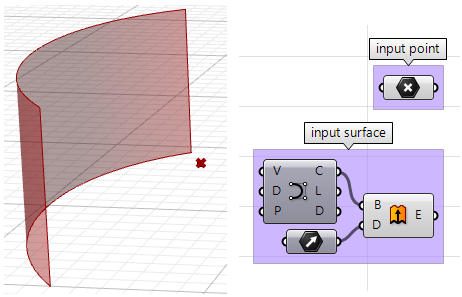
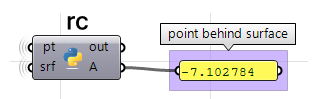
给定一个点和一个曲面,我们该如何确定该点面向曲面的正面还是背面?
输入:
- 一个曲面
- 一个点
参数:
面方向由曲面法向定义,我们需要以下信息:
- 最靠近输入点的曲面位置处的曲面法向向量。
- 从最近点到输入点的矢量。
比较以上两个矢量,如果同向,则点在正面,否则点在反面。
解决方案
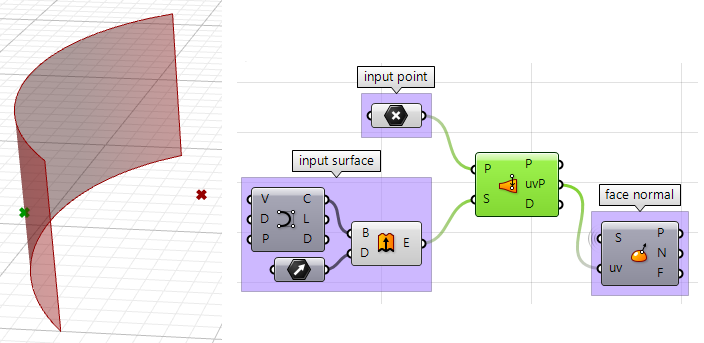
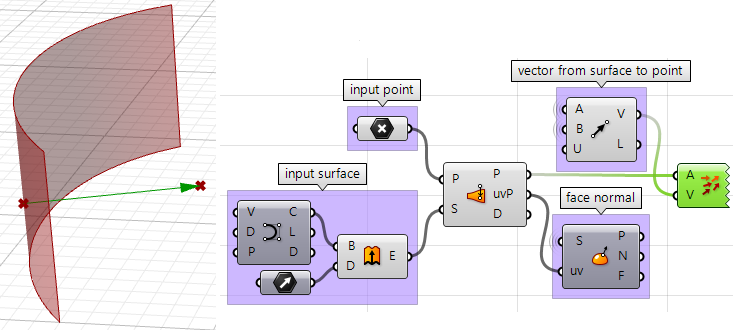
- 使用pull组件找到曲面上输入点的最近点,这将找到最近点的uv坐标,之后我们可以使用这个坐标来确定曲面的法线方向。
- 利用最近点绘制指向输入点的向量,如图:
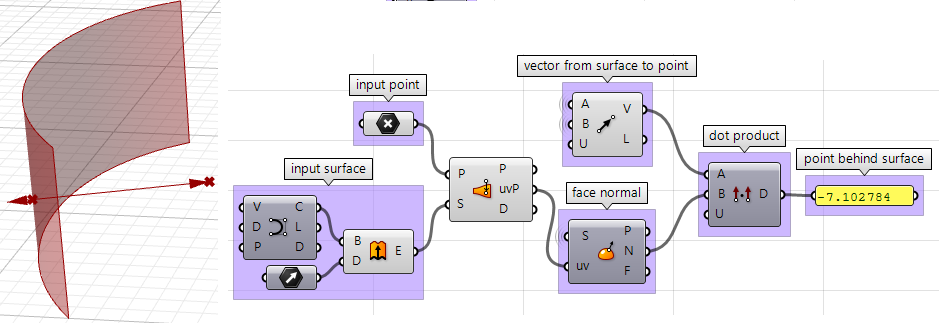
- 现在我们可以利用点积来比较两个向量,如果结果为正,点位于曲面前,结果为负,点位于曲面后。
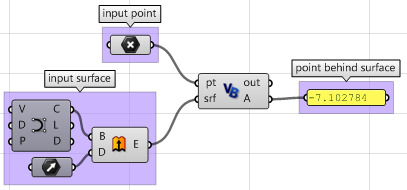
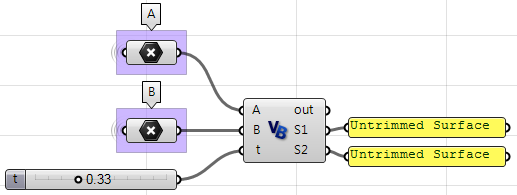
上述步骤也可以使用其他语言解决,如使用GH的VB组件:
Private Sub RunScript(ByVal pt As Point3d, ByVal srf As Surface, ByRef A As Object)
'声明变量
Dim u, v As Double
Dim closest_pt As Point3d
'获取最近点uv
srf.ClosestPoint(pt, u, v)
'获取最近点
closest_pt = srf.PointAt(u, v)
'计算从最近点到输入点的方向
Dim dir As New Vector3d(pt - closest_pt)
'计算曲面法向
Dim normal = srf.NormalAt(u, v)
'计算两向量点积
A = dir * normal
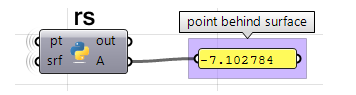
End Sub使用GH的Python组件(利用RhinoScript库):
import rhinoscriptsyntax as rs #导入RhinoScript库
#找最近点uv
u, v = rs.SurfaceClosestPoint(srf, pt)
#获得最近点
closest_pt = rs.EvaluateSurface(srf, u, v)
#计算最近点到输入点向量
dir = rs.PointCoordinates(pt) - closest_pt
#计算曲面法向
normal = rs.SurfaceNormal(srf, [u, v])
#计算两向量点积
A = dir * normal使用GH的Python组件(只使用rhinocommon):
#找最近点
found, u, v = srf.ClosestPoint(pt)
if found:
#获取最近点
closest_pt = srf.PointAt(u, v)
#计算输入点到最近点向量
dir = pt - closest_pt
#计算曲面法向
normal = srf.NormalAt(u, v)
#计算两向量点积
A = dir * normal使用GH的C#组件:
private void RunScript(Point3d pt, Surface srf, ref object A)
{
//声明变量
double u, v;
Point3d closest_pt;
//获取最近点uv
srf.ClosestPoint(pt, out u, out v);
//获取最近点
closest_pt = srf.PointAt(u, v);
//计算输入点和最近点间向量
Vector3d dir = pt - closest_pt;
//计算曲面法向
Vector3d normal = srf.NormalAt(u, v);
//计算两向量点积
A = dir * normal;
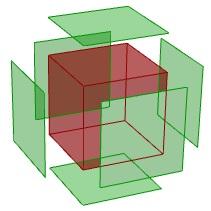
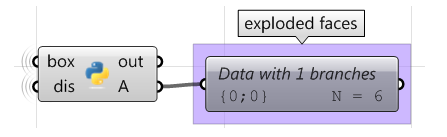
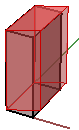
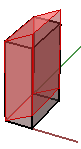
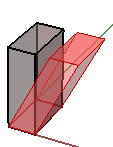
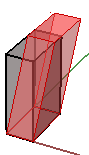
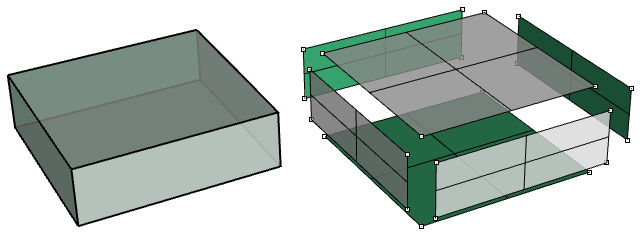
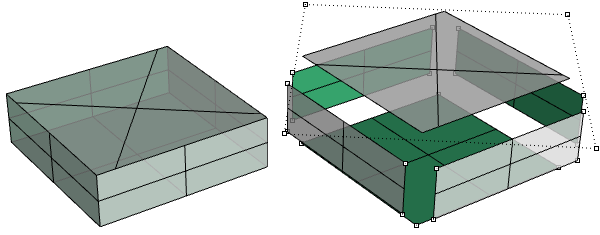
}下面的案例演示如何分解多重曲面。如图是最终分解的立方体的样子:
输入:
参数:
- 思考我们需要知道的所有参数,以便解决本教程的问题
- 分解的中心
- 需要分解的立方体面
- 每个面移动的方向
当我们确定了需要的参数,就要通过拼凑逻辑步骤得到结果,并且整合到解决方案中。
解决方案:
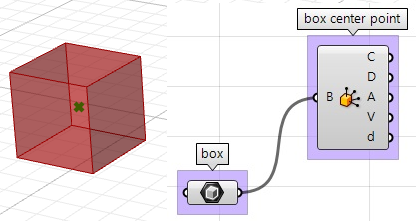
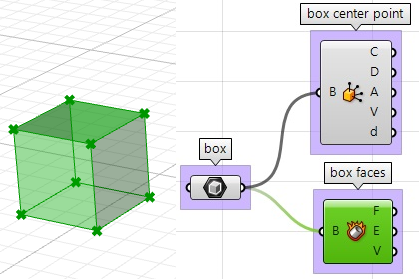
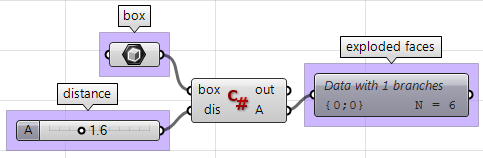
- 使用Box Properties组件找到立方体的中心点:
- 使用Deconstruct Brep组件分解立方体的面:
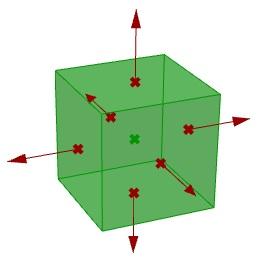
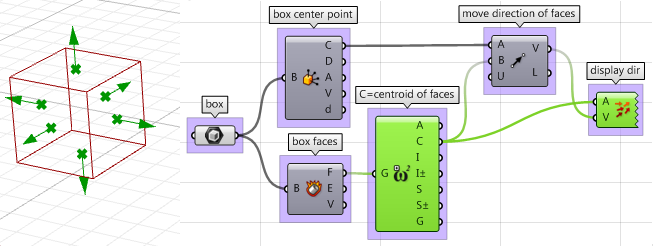
- 一个麻烦的部分是确定移动面的方向。我们需要先找到每个面的中心,然后定义从立方体中心岛每个面中心的方向,如图:
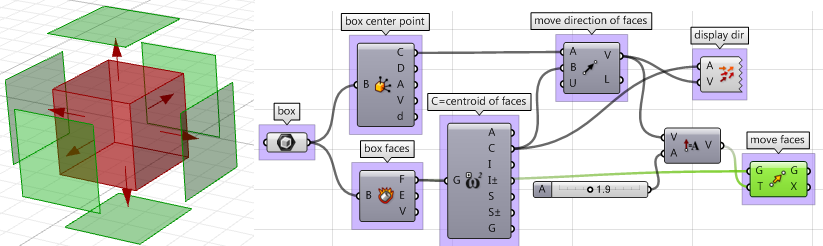
- 一旦我们编写了所有参数的组件,我们就可以使用move组件以适当的方向移动面,只要确保将移动向量设置为需要的长度:
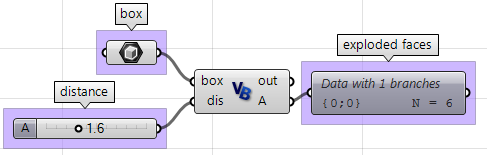
上述步骤也可以使用VB、C#、Python语言解决。下面是解决方案。
使用GH的VB组件:
Private Sub RunScript(ByVal box As Brep, ByVal dis As Double, ByRef A As Object)
'获得实体的中心点
Dim area As Rhino.Geometry.AreaMassProperties
area = Rhino.Geometry.AreaMassProperties.Compute(box)
Dim box_center As Point3d
box_center = area.Centroid
'获得面列表
Dim faces As Rhino.Geometry.Collections.BrepFaceList = box.Faces
'声明变量
Dim center As Point3d
Dim dir As Vector3d
Dim exploded_faces As New List( Of Rhino.Geometry.Brep )
Dim i As Int32
'遍历所有面
For i = 0 To faces.Count() - 1
'提取每个面
Dim extracted_face As Rhino.Geometry.Brep = box.Faces.ExtractFace(i)
'获得每个面的中心
area = Rhino.Geometry.AreaMassProperties.Compute(extracted_face)
center = area.Centroid
'计算每个面移动的方向(从立方体中心到面中心)
dir = center - box_center
dir.Unitize()
dir *= dis
'移动提取的面
extracted_face.Transform(Transform.Translation(dir))
'加入面列表
exploded_faces.Add(extracted_face)
Next
'制定输出的面列表
A = exploded_faces
End Sub使用GH的Python组件(利用RhinoCommon库):
import Rhino
#获得立方体中心点
area = Rhino.Geometry.AreaMassProperties.Compute(box)
box_center = area.Centroid
#获得面列表
faces = box.Faces
#声明变量
exploded_faces = []
#遍历所有面
for i, face in enumerate(faces):
#或则一个面的复制
extracted_face = faces.ExtractFace(i)
#获得每个面的中心
area = Rhino.Geometry.AreaMassProperties.Compute(extracted_face)
center = area.Centroid
#计算每个面移动的方向(从立方体中心到面中心)
dir = center - box_center
dir.Unitize()
dir *= dis
#移动提取的面
move = Rhino.Geometry.Transform.Translation(dir)
extracted_face.Transform(move)
#加入到面列表
exploded_faces.append(extracted_face)
#指定到要输出的面列表
A = exploded_faces使用GH的C#组件:
private void RunScript(Brep box, double dis, ref object A)
{
//获得实体中心
Rhino.Geometry.AreaMassProperties area = Rhino.Geometry.AreaMassProperties.Compute(box);
Point3d box_center = area.Centroid;
//获得面列表
Rhino.Geometry.Collections.BrepFaceList faces = box.Faces;
//声明变量
Point3d center; Vector3d dir;
List<Rhino.Geometry.Brep> exploded_faces = new List<Rhino.Geometry.Brep>();
//遍历所有面
for( int i = 0; i < faces.Count(); i++ )
{
//提取每个面
Rhino.Geometry.Brep extracted_face = box.Faces.ExtractFace(i);
//获得每个面的中心
area = Rhino.Geometry.AreaMassProperties.Compute(extracted_face);
center = area.Centroid;
//计算每个面移动的方向(从立方体中心到面中心)
dir = center - box_center;
dir.Unitize();
dir *= dis;
//移动提取的面
extracted_face.Transform(Transform.Translation(dir));
//加入到面列表
exploded_faces.Add(extracted_face);
}
//指定到要输出的面列表
A = exploded_faces;
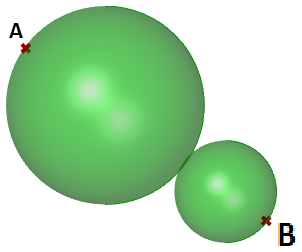
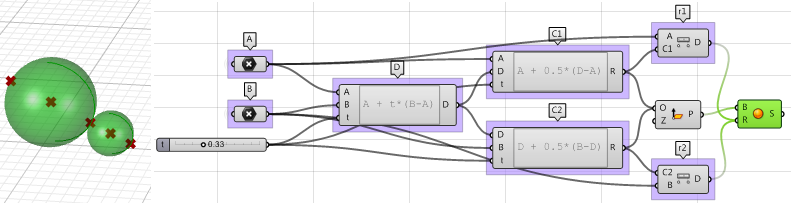
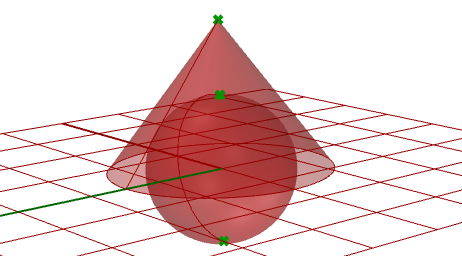
}本实例将演示如何在两个输入点之间创建两个相切球体,结果如图:
输入:
两个点($A$和$B$) 在三维坐标系。
参数:
以下是解决问题需要的参数,两个球体间的切点$D$,是一个参数$t$(在$(0,1)$的开区间)表示A和B之间的点。
- 第一个球体的中心既$AD$的中点$C_1$
- 第二个球体的中心既$BD$的中点$C_2$
- 第一个球体的半径($r_1$)既$AC_1$的长度
- 第二个球体的半径($r_2$)既$BC_2$的长度
解决方案:
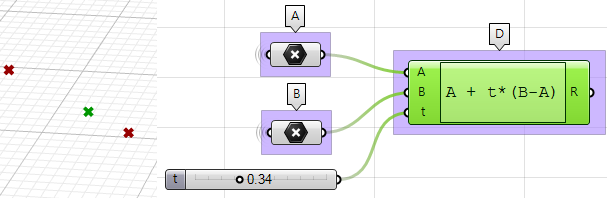
- 使用Expression组件在参数t的定义下定义$AB$之间点$D$,我们使用的表达式基于直线的向量方程:$D=A+t*(B-A)$
我们的表达式就是:
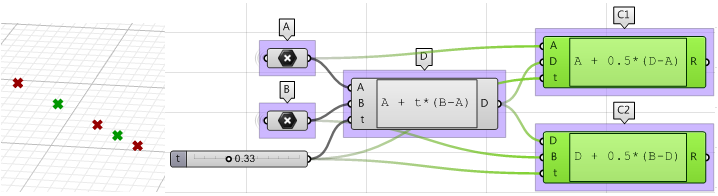
$$A+t*(B-A)$$ 获得$AB$之间的点 - 使用Expression组件利用相同的表达式得到$C_1$和$C_2$
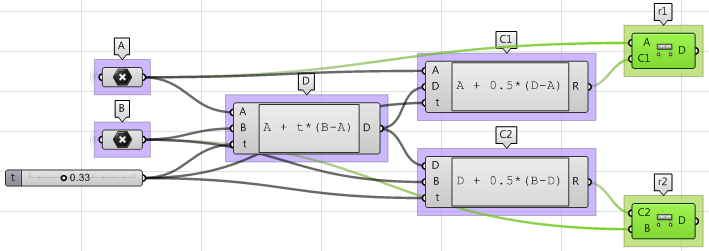
- 使用Distance组件得到两个球体的半径$r_1$和$r_2$
- 最后一步我们从Plane和半径创建球体。
使用GH的VB组件:
Private Sub RunScript(ByVal A As Point3d, ByVal B As Point3d, ByVal t As Double, ByRef S1 As Object, ByRef S2 As Object)
'声明变量
Dim D, C1, C2 As Rhino.Geometry.Point3d
Dim r1, r2 As Double
'获得AB间的点
D = A + t * (B - A)
'获得AD中点
C1 = A + 0.5 * (D - A)
'获得DB中点
C2 = D + 0.5 * (B - D)
'获得球体半径
r1 = A.DistanceTo(C1)
r2 = B.DistanceTo(C2)
'创建球体并输出
S1 = New Rhino.Geometry.Sphere(C1, r1)
S2 = New Rhino.Geometry.Sphere(C2, r2)
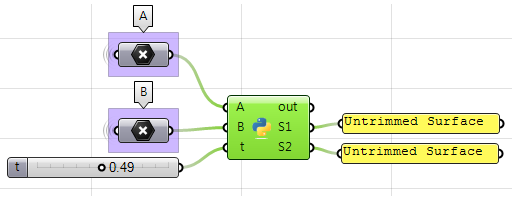
End Sub使用GH的Python组件:
import Rhino
#find a point between A and B
D = A + t * (B - A)
#find mid point between A and D
C1 = A + 0.5 * (D - A)
#find mid point between D and B
C2 = D + 0.5 * (B - D)
#find spheres radius
r1 = A.DistanceTo(C1)
r2 = B.DistanceTo(C2)
#create spheres and assign to output
S1 = Rhino.Geometry.Sphere(C1, r1)
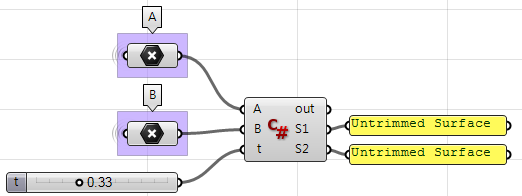
S2 = Rhino.Geometry.Sphere(C2, r2)使用GH的C#组件:
private void RunScript(Point3d A, Point3d B, double t, ref object S1, ref object S2)
{
//declare variables
Rhino.Geometry.Point3d D, C1, C2;
double r1, r2;
//find a point between A and B
D = A + t * (B - A);
//find mid point between A and D
C1 = A + 0.5 * (D - A);
//find mid point between D and B
C2 = D + 0.5 * (B - D);
//find spheres radius
r1 = A.DistanceTo(C1);
r2 = B.DistanceTo(C2);
//create spheres and assign to output
S1 = new Rhino.Geometry.Sphere(C1, r1);
S2 = new Rhino.Geometry.Sphere(C2, r2);
}变换是指移动(也称为平移)、旋转和缩放对象等操作。它们使用矩阵存储在 3D 程序中,矩阵仅是数字组成的矩形数组。使用矩阵可以非常快速地执行多个转换。事实上,[4x4] 矩阵可以表示所有变换。为所有转换提供统一的矩阵维度可以节省计算时间。
$$\begin{array}{rcc} \mbox{matrix}&\begin{array}{cccc} c1& c2&c3&c4\end{array}\\begin{array}{c}row(1)\row(2)\row(3)\row(4)\end{array}& \left[\begin{array}{cr} +&+&+&+\ +&+&+&+\ +&+&+&+\ +&+&+&+\end{array}\right] \end{array}$$
译者注:显然这些变换不包含扭转等复杂变换,矩阵维度指矩阵的行数和列数。
在计算机图形学中,与之最有关的矩阵运算就是矩阵乘法,我们会对矩阵乘法做详细解释。
矩阵乘法用于将变换应用于几何图形。例如我们有一个点,我们令他绕某个轴旋转,我们用一个旋转矩阵乘该点,得到新的旋转后的位置。
$$\begin{array}{ccc} \text{旋转矩阵} & \text{输入点} & \text{旋转点}\\begin{bmatrix}a & b & c & d \e & f & g & h \i & j & k & l \0 & 0 & 0 & 1 \\end{bmatrix}& \cdot\begin{bmatrix}x \y\z\1 \\end{bmatrix}&= \begin{bmatrix}x' \y'\z'\1 \\end{bmatrix}\end{array}$$
大多时候,我们需要对同一个几何物体进行多次变换,例如我们需要移动和旋转 1000 个点,我们可以用以下方法之一。
方法1
- 将移动矩阵乘1000个点来移动这些点。
- 将旋转矩阵乘产生的1000个点来旋转上一步移动的点。
操作次数 = 2000.
译者注:对于矩阵乘法来说,交换律是失效的,也就是$A×B$和
$B×A$ 并不表示相同的意义,所以翻译过程中的乘法顺序会尽量和书写顺序保持一致,但仍需读者时时注意乘法顺序,防止混淆和错误。
方法2
- 将旋转矩阵乘移动矩阵得到组合变换矩阵。
- 将组合矩阵乘 1000 个点在一步之内得到移动和旋转后的点。
操作次数 = 1001.
注意,方法一需要几乎两倍的操作数才能得到相同的结果。虽然方法2非常有效,但当且仅当移动和旋转矩阵都是$[4 \times 4]$矩阵时,运算才成为可能,这就是为什么在计算机图形学中使用$[4 \times 4]$矩阵来表示所有的变换,并且用$[4 \times 1]$的矩阵表示点。
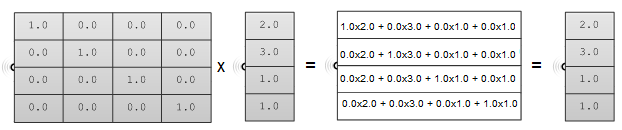
三维建模程序提供了工具来进行变换和矩阵乘法,但如果你对如何使用数学方法对矩阵进行乘法感到好奇,我们提供了一个简单示例,为了令两矩阵相乘,他们必须有匹配的维数.这也意味着第一个矩阵的列数必须等于第二个矩阵的行数.相乘的结果矩阵的行数和列数分别为第一个矩阵的行数和第二个矩阵的列数.例如我们有两个矩阵$M$和$P$,维数分别为$[4 \times 4]$和$[4 \times 1]$,得到的矩阵$M · P$结果的维数为$[4 \times 1]$如下所示:
$$\begin{array}{ccc} M & P & P' \\begin{bmatrix}\color{red}{a} & \color{red}{b} & \color{red}{c} & \color{red}{d} \e & f & g & h \i & j & k & l \0 & 0 & 0 & 1 \\end{bmatrix}& \cdot\begin{bmatrix}\color{red}{x} \\color{red}{y} \\color{red}{z} \\color{red}{1} \\end{bmatrix}&= \begin{bmatrix}\color{red}{x'=ax+by+cz+d1}\y'=ex+fy+gz+h1\z'=ix+jy+kz+l1 \1=0x+0y+0z+11\\end{bmatrix}\end{array}$$
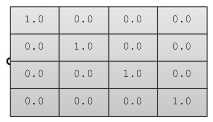
单位矩阵是一个特殊的矩阵,除了对角线上的分量为1外,所有的分量都为0。
单位矩阵的主要性质是单位矩阵乘任意矩阵或0的结果依然是该矩阵或0。
大多数变换都保留了几何物件各部分之间的平行关系。例如,同一直线上点在变换后仍保持共线。此外,一个平面上的点在变换后保持共面。这种类型的变换称为仿射变换。
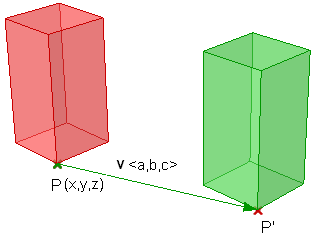
将点从起始位置移动某个向量的计算如下:
假设:
那么我们有:
点以$[4 \times 1]$矩阵格式表示,最后一行插入1。例如,点$P(x,y,z)$表示如下:
$$\begin{bmatrix}x\y\z\1\\end{bmatrix}$$
使用$[4 \times 4]$矩阵进行变换(这被称作齐次坐标系下的变换),而不是$[3 \times 3]$矩阵,可以表示包括移动在内的所有变换。平移矩阵的一般格式为:
$$\begin{bmatrix}1 & 0 & 0 & \color{red}{a1} \0 & 1 & 0 & \color{red}{a2} \0 & 0 & 1 & \color{red}{a3} \0 & 0 & 0 & 1 \\end{bmatrix}$$
例如,为了使用向量
如果我们使用矩阵形式,并将平移矩阵输入点,我们得到的点位置如下所示:
$$\begin{bmatrix}1 & 0 & 0 & 2 \0 & 1 & 0 & 2 \0 & 0 & 1 & 2 \0 & 0 & 0 & 1 \\end{bmatrix}\cdot\begin{bmatrix}2 \3\1\1 \\end{bmatrix}= \begin{bmatrix}(12 + 03 + 01 + 21) \(02 + 13 + 01 + 21)\(02 + 03 + 11 + 21)\(02 + 03 + 01 + 11)\\end{bmatrix}=\begin{bmatrix}4 \5\3\1 \\end{bmatrix}$$
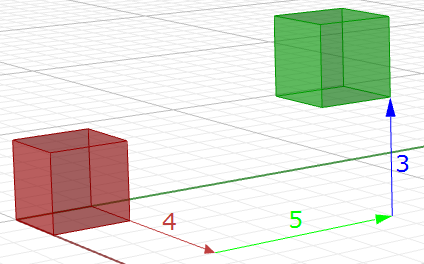
类似的,任意几何物件都是通过构造平移矩阵乘点来平移的。例如我们有一个八个角点定义的立方体,我们想在x方向移动4个单位,y方向移动5单位,z方向移动3单位,我们必须用平移矩阵乘所有八个角点得到新的角点以此得到新的平移后的立方体。
$$\begin{bmatrix}1 & 0 & 0 & 4\ 0 & 1 & 0 & 5 \0 & 0 & 1 & 3 \0 & 0 & 0 & 1 \\end{bmatrix}$$
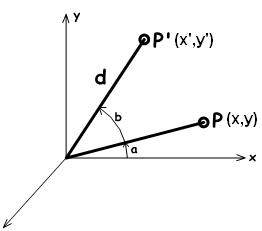
图19:平移所有方框角点本节介绍如何使用三角函数计算绕 z 轴和原点的旋转,然后推导旋转变换的一般矩阵格式。
在$xy$平面取一点P(x,y)并且旋转一个角度$$b$$. 我们由图易得:
用三角恒等式(和角公式)展开$x'$和$y'$得到角的正弦和余弦值:
由(1)和(2)得:
沿世界坐标z轴旋转的矩阵如下:
$$\begin{bmatrix}\color{red}{\cos{b}} & \color{red}{-\sin{b}} & 0 & 0 \\color{red}{\sin{b}} & \color{red}{\cos{b}} & 0 & 0 \0 & 0 & 1 & 0 \0 & 0 & 0 & 1 \\end{bmatrix}$$
沿世界坐标x轴旋转b弧度的矩阵如下:
$$\begin{bmatrix}1 & 0 & 0 & 0 \0 & \color{red}{\cos{b}} & \color{red}{-\sin{b}} & 0 \0 & \color{red}{\sin{b}} & \color{red}{\cos{b}} & 0 \0 & 0 & 0 & 1 \\end{bmatrix}$$
沿世界坐标y轴旋转b弧度的矩阵如下:
$$\begin{bmatrix}\color{red}{\cos{b}} &0 & \color{red}{\sin{b}} & 0 \0 & 1 & 0 & 0 \\color{red}{-\sin{b}} & 0 &\color{red}{\cos{b}} & 0 \0 & 0 & 0 & 1 \\end{bmatrix}$$
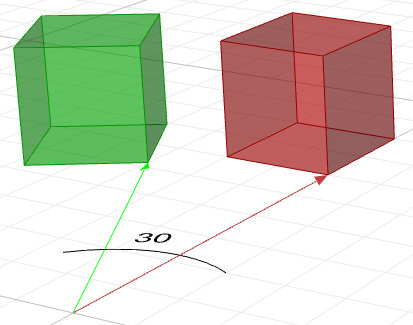
已一个立方体为例,我们将其旋转30度,我们需要做如下操作:
-
构造一个30度的旋转矩阵,使用沿Z轴旋转的通用形式,旋转矩阵如下:
$$\begin{bmatrix}0.87 & -0.5 & 0 & 0 \0.5 & 0.87 & 0 & 0 \0 & 0 & 1 & 0 \0 & 0 & 0 & 1 \\end{bmatrix}$$
-
将旋转矩阵乘输入的几何物件,如果针对立方体,乘每个角点,找到立方体的新位置。
为了缩放几何物件,我们需要一个比例因子和一个中心。比例因子可以在 x、y 和 z 方向上均匀缩放,也可以在每个维度上是独立的。
缩放点可以使用以下公式:
或:
这是缩放变换的矩阵形式,假设缩放中心是世界坐标原点$(0,0,0)$。
$$\begin{bmatrix}\color{red}{Scale-x} & 0 & 0 & 0 \0 & \color{red}{Scale-y} & 0 & 0 \0 & 0 & \color{red}{Scale-z} & 0 \0 & 0 & 0 & 1 \\end{bmatrix}$$
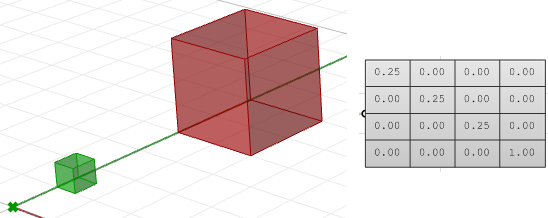
例如我们为了将一个立方体相对世界坐标原点缩放0.25,那么缩放矩阵如下:
图21:缩放几何三维的剪切是沿着某一个轴不变另外垂直的另外一个轴方向变化的变换。例如,沿 z 轴的剪切变换不会改变z轴的尺寸,但会改变x和y轴方向的尺寸.下面是一些例子:
-
保持y轴方向不变,x、z方向剪切
$$\begin{bmatrix}1.0 &\color{red}{0.5} & 0.0 & 0.0 \ 0.0 & 1.0 & 0.0 & 0.0 \ 0.0 & 0.0 & 1.0 & 0.0 \ 0.0 & 0.0 & 0.0 & 1.0 \\end{bmatrix}$$
$$\begin{bmatrix}1.0 & 0.0 & 0.0 & 0.0 \ 0.0 & 1.0 & 0.0 & 0.0 \ 0.0 &\color{red}{0.5} & 1.0 & 0.0 \ 0.0 & 0.0 & 0.0 & 1.0 \\end{bmatrix}$$
-
保持x轴方向不变,y、z方向剪切:
$$\begin{bmatrix}1.0 & \color{red}{0.5} & 0.0 & 0.0 \ 0.0 & 1.0 & 0.0 & 0.0 \ 0.0 & 0.0 & 1.0 & 0.0 \ 0.0 & 0.0 & 0.0 & 1.0 \\end{bmatrix}$$
$$\begin{bmatrix}1.0 & 0.0 & 0.0 & 0.0 \ 0.0 & 1.0 & 0.0 & 0.0 \ 0.0 & \color{red}{0.5} & 1.0 & 0.0 \ 0.0 & 0.0 & 0.0 & 1.0 \\end{bmatrix}$$
-
保持z轴方向不变,x、y方向剪切:
$$\begin{bmatrix}1.0 & 0.0 & \color{red}{0.5} & 0.0 \ 0.0 & 1.0 & 0.0 & 0.0 \ 0.0 & 0.0 & 1.0 & 0.0 \ 0.0 & 0.0 & 0.0 & 1.0 \\end{bmatrix}$$
$$\begin{bmatrix}1.0 & 0.0 & 0.0 & 0.0 \ 0.0 & 1.0 & \color{red}{0.5} & 0.0 \ 0.0 & 0.0 & 1.0 & 0.0 \ 0.0 & 0.0 & 0.0 & 1.0 \\end{bmatrix}$$
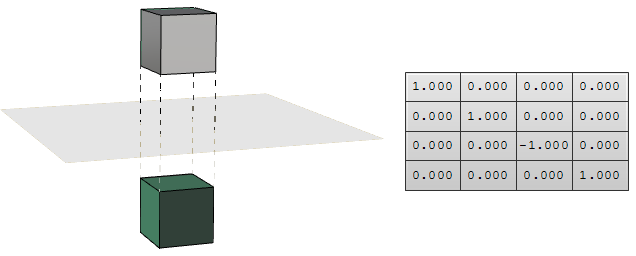
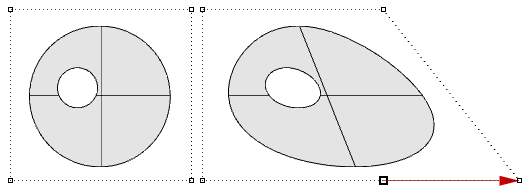
镜像变换在直线或平面上创建对象的镜像。二维物体是通过一条直线镜像的,而三维物体是通过一个平面镜像的。请记住,镜像变换翻转了几何面的法线方向.
图23:使用世界坐标xy平面镜像变换的矩阵,面法向被翻转直观说,一个空间点$P(x,y,z)$在xy平面上的投影点$P_{xy} (x,y,0)$只需设置$z$为0即可。同理$P$在xz平面的投影点是$P_{xz}(x,0,z)$。当投影到yz平面时,$P_{xz} = (0,y,z)$。我们称这些为正交投影。
如果我们有一条曲线作为输入,我们应用平面投影变换,将得到一条曲线投影到那个平面上。下面是一个用矩阵格式投影到 xy 平面的曲线的例子。
注: NURBS 曲线(下一章解释)使用控制点来定义曲线。投射一条曲线等于投射它的控制点。
译者注:有关Nurbs投影不变性的证明的扩展阐述可参考如下链接:
https://pages.mtu.edu/~shene/COURSES/cs3621/NOTES/spline/NURBS/NURBS-property.html
$$\begin{bmatrix}1.0 & 0.0 & 0.0 & 0.0 \ 0.0 & 1.0 & 0.0 & 0.0 \ 0.0 & 0.0 & \color{red}{0.0} & 0.0 \ 0.0 & 0.0 & 0.0 & 1.0 \\end{bmatrix}$$ $$\begin{bmatrix}1.0 & 0.0 & 0.0 & 0.0 \ 0.0 & \color{red}{0.0} & 0.0 & 0.0 \ 0.0 & 0.0 & 1.0 & 0.0 \ 0.0 & 0.0 & 0.0 & 1.0 \\end{bmatrix}$$ $$\begin{bmatrix} \color{red}{0.0} & 0.0 & 0.0 & 0.0 \ 0.0 & 1.0 & 0.0 & 0.0 \ 0.0 & 0.0 & 1.0 & 0.0 \ 0.0 & 0.0 & 0.0 & 1.0 \\end{bmatrix}$$
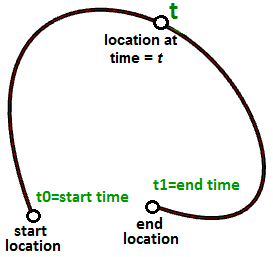
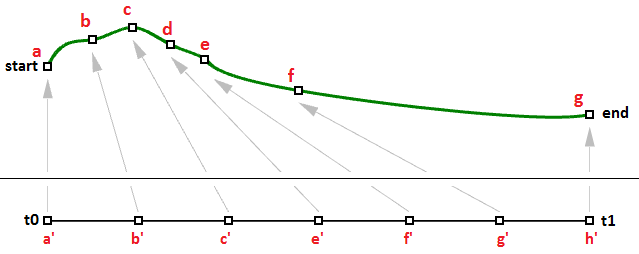
假设您每个工作日都从家里到工作地点。您早上 8:00 出发,9:00 到达。在 8:00 到 9:00 之间的每个时间点,您都会在沿途的某个位置。如果您在旅途中每分钟绘制一次位置,则可以通过连接绘制的 60 个点来定义家庭和工作之间的路径。假设您每天以完全相同的速度行驶,则在 8:00 您将在家(起始位置),在 9:00 您将在工作(结束位置),在 8:40 您将在与第 40 个绘图点完全相同的路径上的位置。恭喜,您刚刚定义了第一条参数曲线!您已使用时间作为参数来定义路径,因此您可以将路径曲线称为参数化曲线。您从开始到结束(8 到 9)花费的时间间隔称为曲线区间或曲线域。
我们可以用一些参数如$t$来描述参数曲线上点的位置的$x$、$y$、$z$,如下所示:
其中:
我们之前学习过,直线的参数方程使用$t$定义如下:
其中:
由此我们可以使用一个介于实数$t0$和$t1$之间的参数$t$和一个沿线段方向的单位向量$\mathbf{\vec v}$来描述线段的参数方程
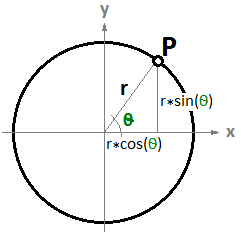
另一个例子是圆。$xy$平面上圆的参数方程:中心位于原点$(0,0)$,角度参数$t$范围在0和2𝜋弧度之间。
$$ x/r = cos(t)$$
由于:
我们有:
故该参数方程表示一个圆。
曲线上的参数表示该曲线上某个点的地址。如前所述,您可以将参数曲线视为在一定时间内以固定或可变速度在两点之间行进的路径。如果行进需要$T$时间,则参数$t$表示曲线上的位置对应的T时间段内的时间。
如果在$A$、$B$两点之间有一直线路径(线段),且$\mathbf{\vec v}$是从$A$到$B$的向量($\mathbf{\vec v} = B - A$),则可以用参数方程来表示$A$、$B$两点之间的所有点$M$,如下所示:
其中:
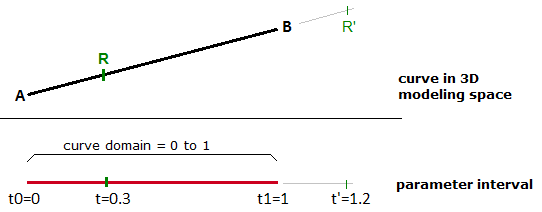
在这种情况下,$t$值的范围(0到1)被称为曲线区间或曲线域。如果$t$是区间外的值(小于0或大于1),则结果点$M$将位于线段$\overline{AB}$之外。
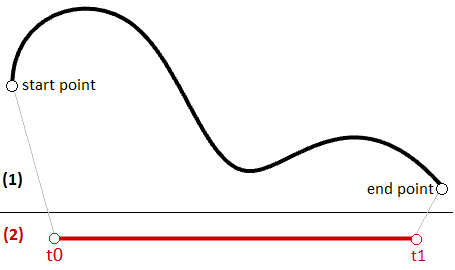
图25:三维空间和参数区间中的线段的参数曲线同样的原理适用于任意的参数曲线。曲线上的任意一点都可以在定义曲线的参数区间内使用$t$值进行计算。区间的起始位置的值通常称为$t0$,结束位置的值称为$t1$。
图26:三维空间(1)和参数区间(2)中的曲线译者注:作者在这里大量的重复使用和混用区间和域(domain and interval )在意思相同的情况下,译者行文将统一使用区间一词。
曲线区间的定义为计算该曲线内点的参数范围。区间通常用两个实数来描述区间限制,以(min to max)或(min,max)的形式表示。区间限制可以是任意两个值,这些值可能与曲线的实际长度相关,也可能与曲线的实际长度无关。在递增区间中,区间min参数的计算结果为曲线的起点,区间max的计算结果为曲线的终点。
图27:曲线区间介于任意两数之间更改曲线区间被称为曲线的重新参数化。比如,一个常见的操作是将曲线区间更改为(0 to 1)。曲线的重新参数化不会影响到曲线形状。就如通过跑步代替走路改变路径上的时间并不会改变路径形状本身一样。
图28:归一化曲线区间到0到1递增区间意味着区间的最小值指向曲线起点,区间通常是递增的,但也不绝对。
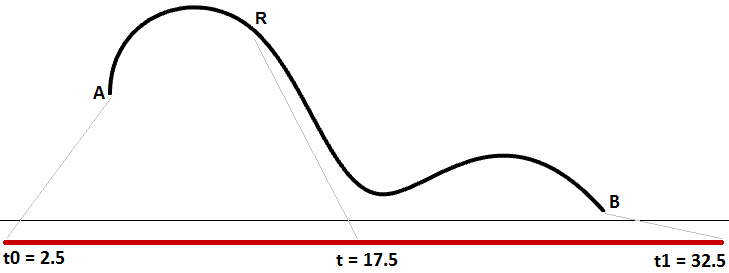
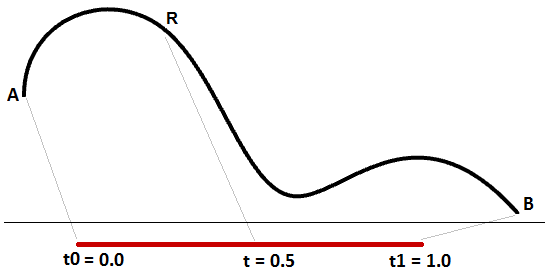
我们能知道到曲线区间是三维曲线内所有点对应参数值的范围,但是区间中值并不能保证计算得到曲线的中点。如图30所示。
译者注:这里原文为如图29,可能为笔误。
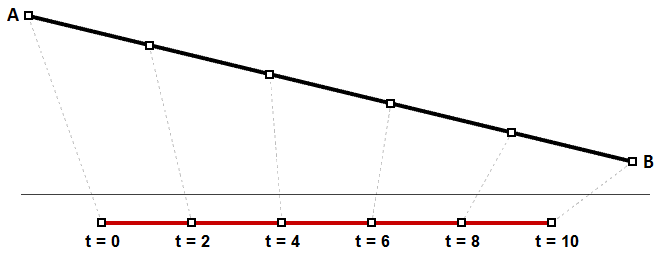
我们可以将曲线的均匀参数化视为以恒定速度行进的路径。两点脸成的一阶直线就是一个示例,其中相等的参数间隔转换为曲线上相等的长度间隔。这是一种特殊情况,其中相等的参数间隔在三维曲线上计算为相等的间隔。
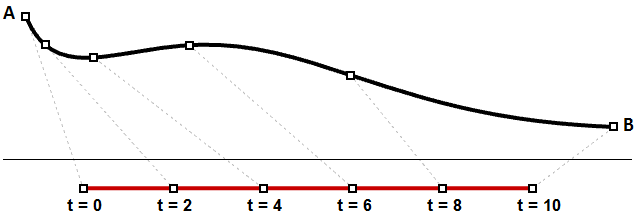
图29:一阶直线相等的参数间隔计算为相等的曲线长度但速度更可能随着路径变化。假设走一条路需要30分钟,那么很难恰巧在第15分钟走完路程的一半。图30展示了这种情况,相等的参数间隔在三维曲线上有不一致的长度。
图30:相等的参数间隔通常不会转换为曲线上的相等距离你可能需要计算三维曲线上根据曲线长度定义比例的点,如你可能需要将曲线划分为等长的曲线段,一般来说建模软件会提供根据曲线长度计算曲线上点的工具。
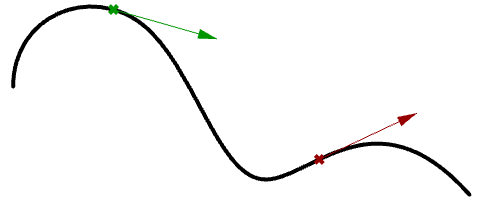
切向量是曲线在任何参数(或曲线上的点)处于在该点接触曲线但不相交的向量。切向量的斜率方向等价于同一点处曲线的斜率方向。下面是曲线在两个参数上该点的切线。
图31:曲线的切线译者注:
在日常和学术交流中,切向量和切线经常混用,严格意义上切向量仅是曲线上该点的方向,但是切线还隐含了该向量从曲线上当前点出发的含义。在本书中两者概念并不做严格区分。
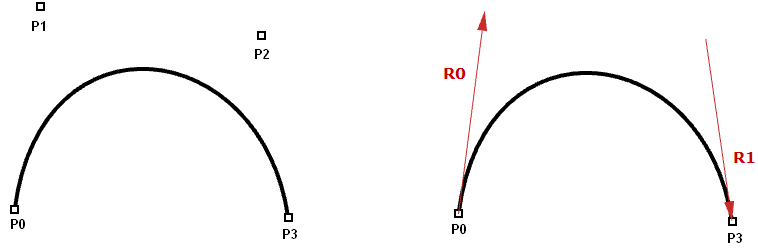
Hermite和Bezier曲线是由四个参数确定的三次多项式曲线的两个示例。Hermite曲线由的两个端点和两个切向量确定,而Bezier曲线由四个点定义。虽然它们在数学上有所不同,但它们具有相似的特征和局限性。
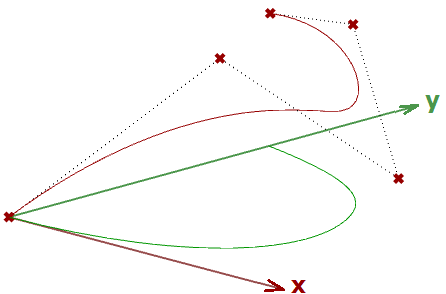
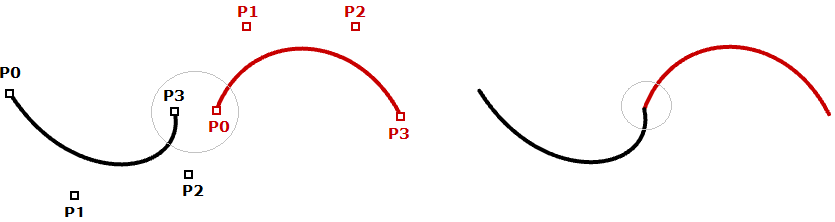
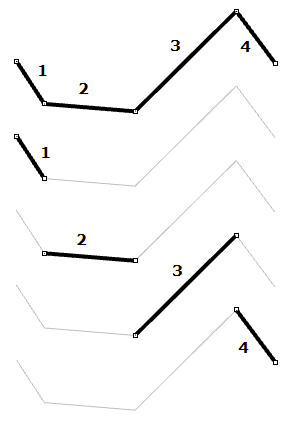
图32:三次多项式曲线:Bezier曲线(左)和Hermite曲线(右)大多数情况下,曲线由多个曲线段组成,这就要求我们制作分段的三次曲线。下面是分段Bezier曲线的图示,该曲线使用七个点创建了两端三次曲线。请注意,曲线仅是连接到一起,并不平滑连续。
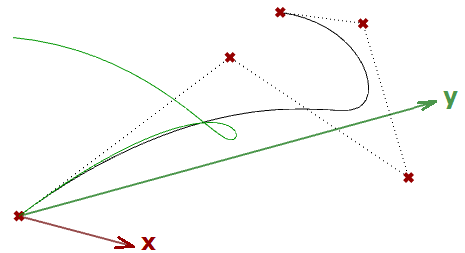
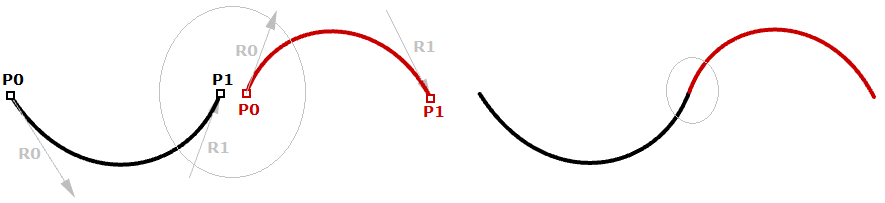
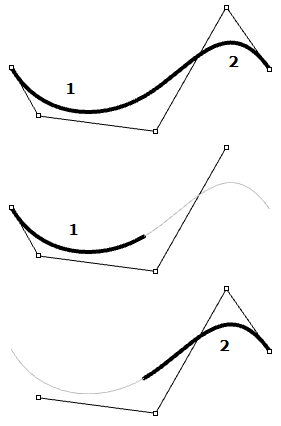
图33:两个Bezier曲线段共用端点尽管Hermite曲线使用同Bezier曲线相同数量的参数(四个参数定义一条曲线),但它们提供了曲线切线的附加信息,这些信息也可以与下一条曲线共享,以创建更平滑的曲线,同时减少总存储空间,如下所示。
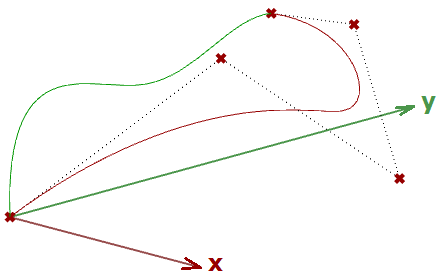
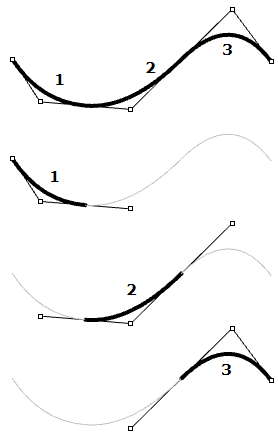
图34:两个Hermite曲线段共用一个点和一个切线非均匀有理 B 样条曲线(NURBS)是一种强大的曲线表示,可保持更平滑、更连续的曲线。曲线段之间共享更多控制点,以更少的存储空间实现更平滑的曲线。
图35:两个3次NURBS曲线段共享三个控制点。NURBS曲线和曲面是Rhino用来表示几何形状的主要数学表示。本章稍后将详细介绍NURBS曲线特性和组成。
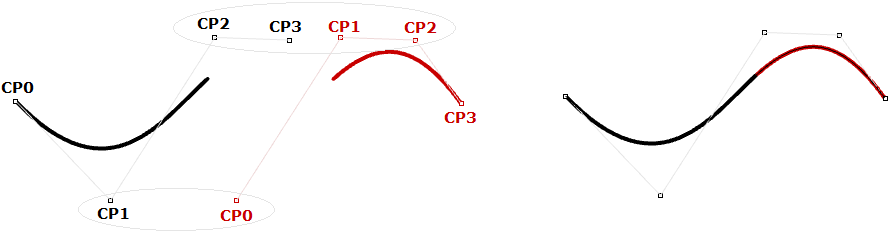
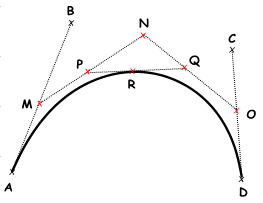
de Casteljau 算法以其发明者 Paul de Casteljau 的名字命名,使用递归方法计算贝塞尔曲线。算法步骤可以总结如下:
输入:
定义曲线的四个点$ABCD$和曲线区间内的参数$t$。
输出:
和参数$t$对应的曲线上的点$R$。
步骤:
- 在线段$$\overline{AB}$$上找到$t$对应的点$M$。
- 在线段$$\overline{BC}$$上找到$t$对应的点$N$。
- 在线段$$\overline{CD}$$上找到$t$对应的点$O$。
- 在线段$$\overline{MN}$$上找到$t$对应的点$P$。
- 在线段$$\overline{NO}$$上找到$t$对应的点$Q$。
- 在线段$$\overline{PQ}$$上找到$t$对应的点$R$。
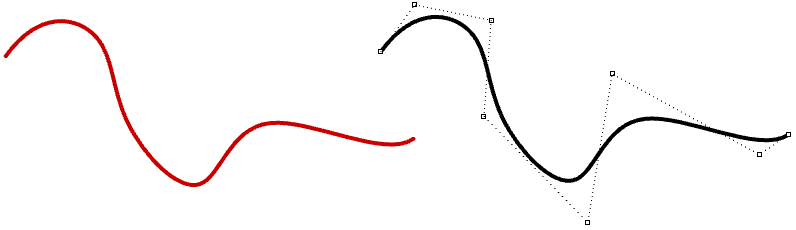
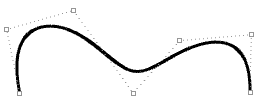
NURBS是一种数学上精确表示曲线的方式,具有直观的可编辑性。使用NURBS表示自由曲线曲面很容易并且其控制结构使得编辑变得容易并可控。
图36:非均匀有理B样条及其控制结构对使用NURBS建模软件的人来说,对NURBS的基础了解是必要的。NURBS曲线有四个主要特性:阶数、控制点、节点列表和计算规则。对于有兴趣更深入研究NURBS的人来说,下附一些书籍和参考资料。
曲线的阶数是正整数,Rhino允许任何大于等于1阶的曲线。1、2、3和5阶曲线是最常用的,但是4阶和5阶以上的阶数在实际作业中并不常用,下面列出一些常见曲线及度数:
译者注:
曲线的阶数本质是曲线对应的有理多项式的次数。
故在翻译时当形容多项式时会翻译成三次多项式曲线,在仅涉及曲线时会翻译成三阶Bezier曲线。
在部分中文资料里会把Nurbs曲线的Order翻译为阶数,Rhino官方的资料里Order翻译为次数,其值为Degree+1。但又会和多项式的次数混淆。
译者在这里不持立场,统一只使用Degree作为阶数而尽量不出现次数的概念(除非明确的涉及多项式的描述)。
NURBS曲线的控制点是至少(阶数+1)个点的列表。改变 NURBS 曲线形状的最直观方法是移动其控制点。
影响 NURBS 曲线中每个子曲线段的控制点数由曲线的阶数定义。例如,阶数为1的曲线中的每个子曲线段仅受两个端控制点的影响。在2阶曲线中,每个子曲线段受三个控制点影响,依此类推。
译者注,在大多数文献中,对span的翻译是跨度,但是相对不太直观,译者将其翻译为子曲线段。
1阶曲线的所有控制点都在曲线上。在 1阶NURBS曲线中,两个(阶数+1)控制点定义一个子曲线段。使用五个控制点,曲线有四个子曲线段。
圆形和椭圆是二阶曲线的示例。在 2阶NURBS曲线中,三个(阶数+1)控制点定义一个子曲线段。使用五个控制点,曲线有三个子曲线段。
3阶曲线的控制点通常不接触曲线,但开放曲线的端点除外。在 3阶NURBS曲线中,四个(阶数+1)控制点定义一个子曲线段。使用五个控制点,曲线有三个子曲线段。
每个控制点都有一个关联的数字,称为权重。除少数例外,权重应为正数。当所有控制点的权重相同时,通常为 1,则该曲线称为非有理曲线。直观地说,您可以将权重视为每个控制点的引力。控制点的相对权重越高,曲线越接近该控制点。
译者注:
非有理是指曲线的表达式是多项式而非有理式,不建议翻译和使用为无理。
值得注意的是,最好避免改变曲线权重。改变权重很少能给出期望的结果,同时它在求曲线交点等操作中引入了许多计算难题。使用有理曲线的唯一充分理由是表示无法以其他方式绘制的曲线,例如圆和椭圆。
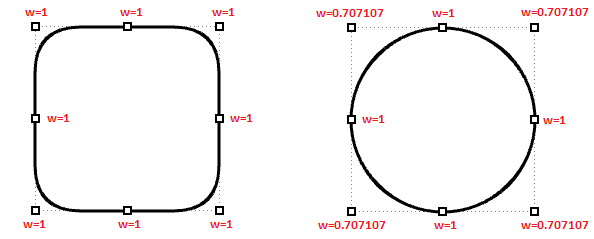
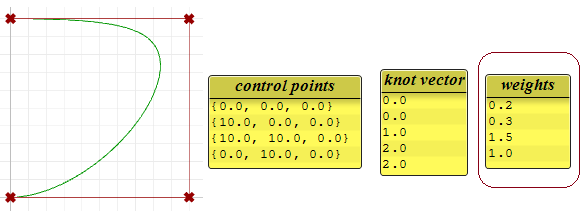
图37:不同权重的控制点对结果曲线的影响。 左边是非有理曲线,控制点权重一致。 右边是一条有理曲线圆,角部控制点的权重小于1。译者注:
90度圆弧控制点中间点的权重正好为$\sqrt{2}/2\approx0.707107$。
圆弧控制点的中间点的权重和控制点连线的夹角有关,具体证明可自行深入了解。
每一条NURBS曲线都有一个与之关联的数字列表,我们称之为节点列表(有时也称为节点向量)。节点解释起来有些抽象,使用建模软件时,我们无需手动设置节点列表,下面附一些对了解节点列表有意义的内容。
译者注:
Knot翻译为节点,Knots一般指节点列表,但二者经常混用。
节点本身只是一个节点列表中的数字,使用节点一词有轻微误导之嫌,但暂未找到更好的处理方式,故沿用。
部分资料Knot翻译为结,把Knot Vector翻译为结点向量,本翻译版本和Rhino官方中文资料保持一致,不采用这种方式。
节点列表是位于曲线区间内的参数值的非递减列表。在 Rhino 中,节点列表长度比控制点个数多阶数-1。即节点列表长度等于控制点数量加上曲线阶数减 1。
|knots| = |CVs| + Degree - 1
节点列表长度=控制点数量+阶数-1
译者注:根据算法不同,不同软件对节点数量有不同的实现。
一般来说,对于非周期曲线,节点向量的第一个值等于曲线区间最小值,节点向量第二个值等于区间最大值。
译者注:周期曲线的内容见下文
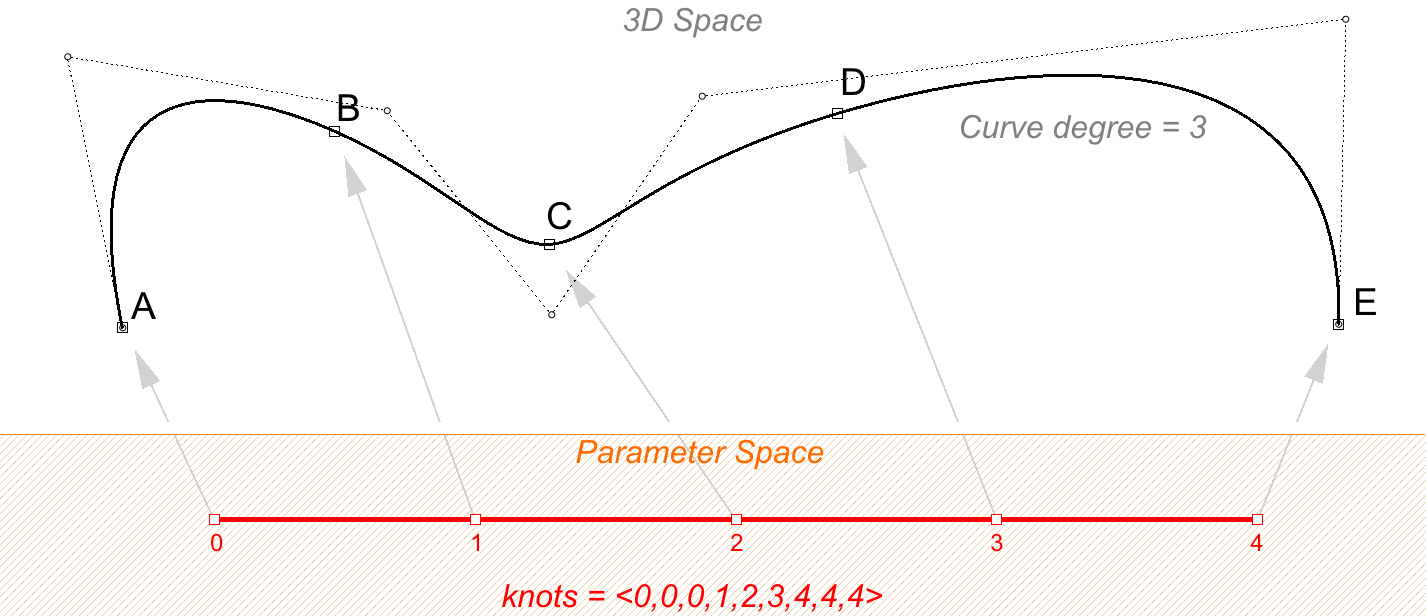
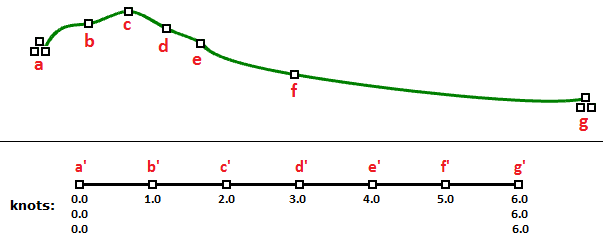
例如一个具有七个控制点且曲线区间为0到4的开放的三阶NURBS曲线的节点列表类似于$<0,0,0,1,2,3,4,4,4>$
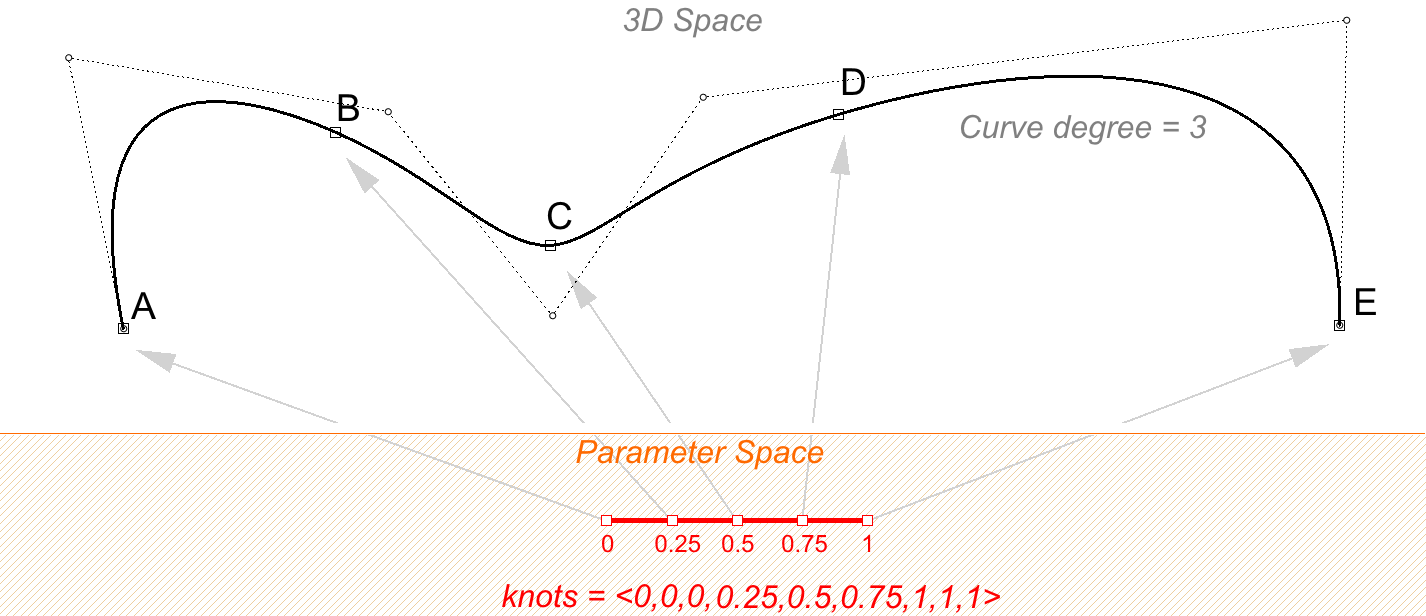
图38:控制点、节点列表长度和阶数的关系缩放节点列表中的值不会影响曲线形状,如果将曲线区间从0-4修改为0-1,节点列表会缩放,但曲线形状不会改变。
图39:缩放节点列表后的曲线节点的重复数量是指相同的值在节点列表中出现的次数,节点重复数量不能大于曲线阶数,重复数量可以控制节点对应参数位置曲线的连续性。
完全重复节点的重数等于曲线阶数,在该节点对应的参数值处,曲线和控制点重合。
例如,钳位的开放曲线在曲线末端有完全重复节点。这正是末端控制点和曲线端点重合的原因,非端点除的重节点僵使曲线在对应参数位置控制点和曲线重合。
译者注:clamped curve 指用端点的重节点将曲线端点“夹”到控制点的曲线。虽然感觉不太恰当,但也没有更合适的翻译了。
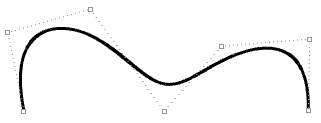
下面两条线具有相同的控制点位置和数量,但有不同的节点列表和曲线形状。
阶数=3
控制点数量 =7
节点列表长度=9
曲线区间(0到4)
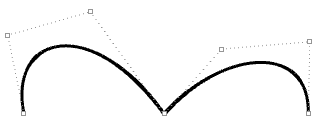
阶数=3
控制点数量 =7
节点列表长度=9
曲线区间(0到4)
Note
中间的完全重复节点会产生纽结,曲线经过了关联的控制点。
单一节点只在节点列表中只出现一次的节点,一般出现在节点列表的内部,也就是非端点的位置。
图39:夹紧曲线在起点和终点具有完整重复节点,内部的节点都是单一节点均匀节点列表满足以下条件。
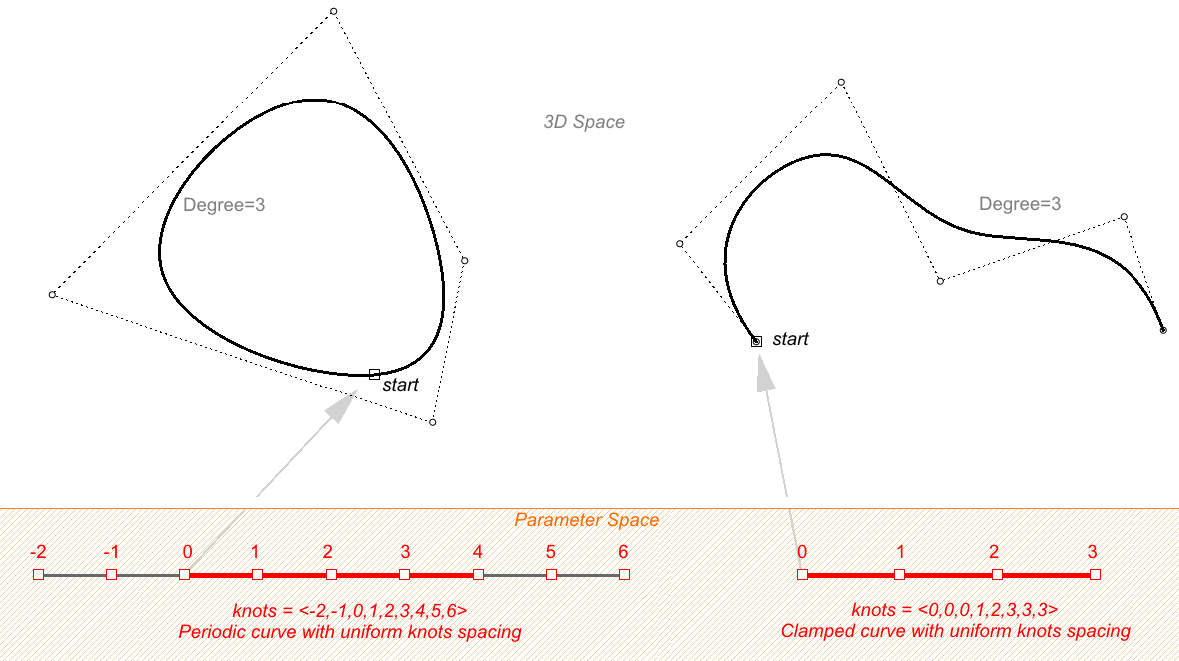
节点列表已完全重复节点开始,然后是单一节点,最后又是完全重复节点,这些节点的值满足等差序列并且递增。典型的是上一节说的钳位的开放曲线。稍后我们将看到周期曲线,他有不同的节点形式。
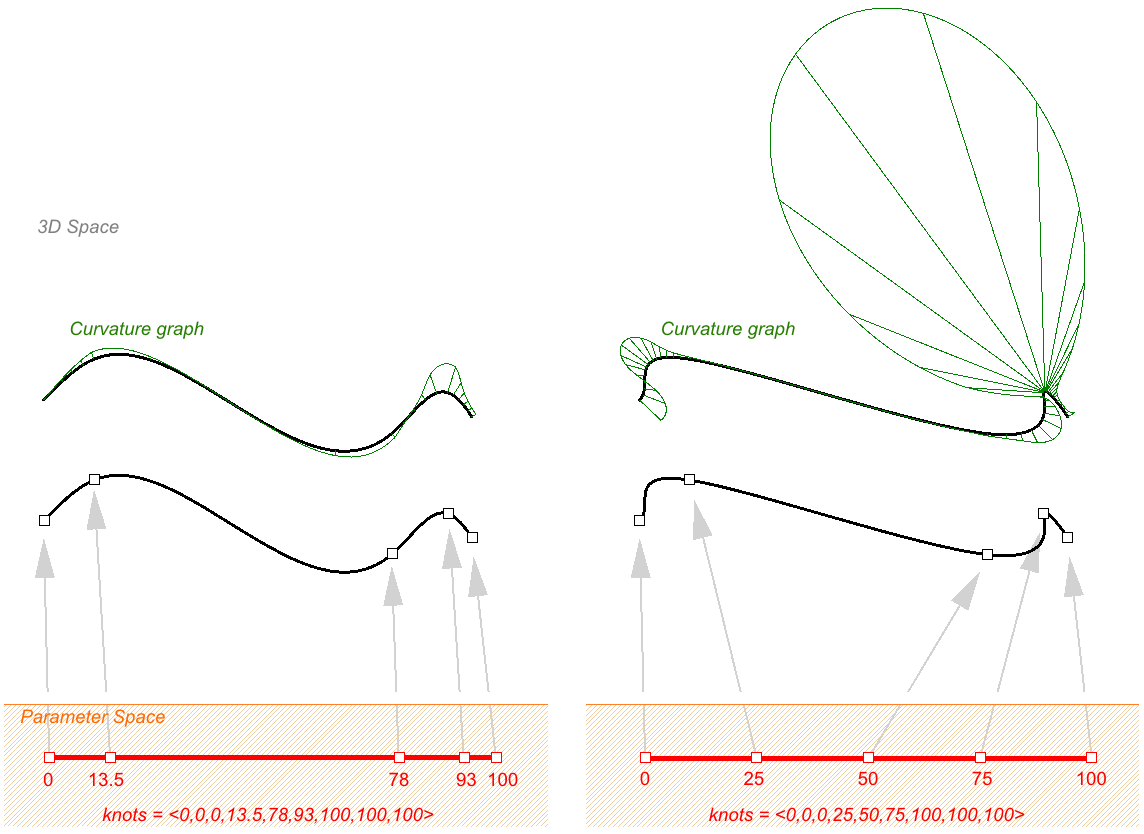
图40:均匀节点列表意味着结之间的间距是恒定的,但钳位曲线除外,它们在开始和结束时可以具有完整的完全重复节点,并且仍然被认为是均匀的。左边的曲线是周期性的(闭合,没有扭结),右边的曲线是钳位的(打开的)。允许NURBS曲线在节点间具有不同的间距有助于控制曲线曲率,已创建更顺滑的曲线,已下图为例,左侧使用非均匀节点列表构造曲线,右侧使用均匀节点列表构造曲线,一般来说如果NURBS曲线的节点值之间的间距和控制点之间的距离成正比,曲线会更顺滑。
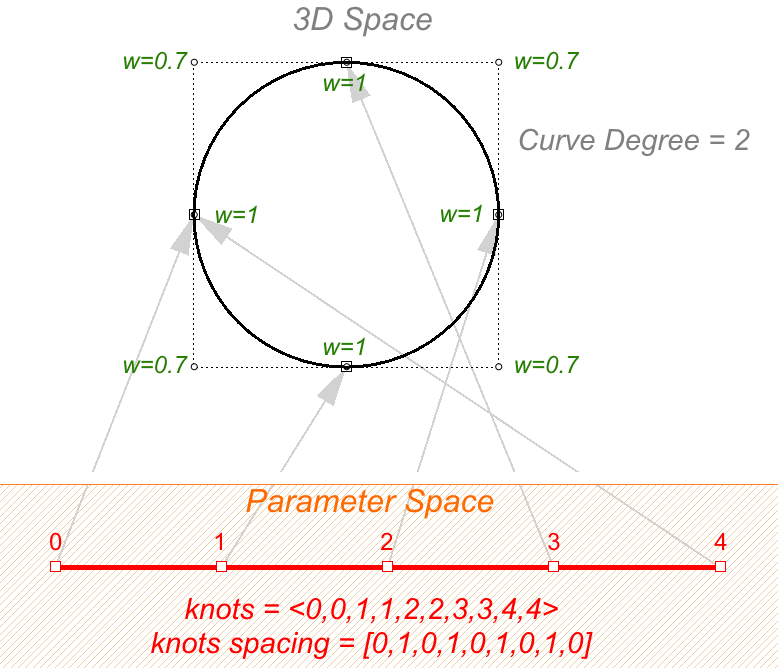
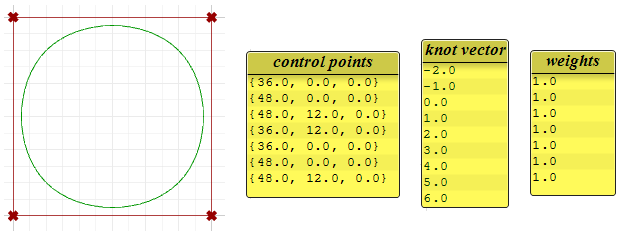
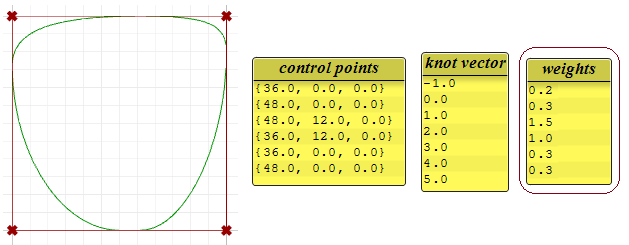
图41:非均匀节点列表可以帮助平滑曲线一个既非均匀又有理的曲线示例是NURBS圆,下图是具有九个控制点节点列表长度为10的2阶曲线,曲线区间为0到4,节点间距在0和1之间来回横跳。
节点列表= <0,0,1,1,2,2,3,3,4,4> —(内部的完全重复节点)
节点间距 = [0,1,0,1,0,1,0,1,0] — (非均匀)
图42:非均匀有理曲线示例NURBS圆计算规则使用了一个考虑阶数,控制点,节点向量的数学公式,该函数输入曲线区间内的一个数返回一个点。
使用该公式,函数可以计算曲线参数并且生成对应的点。参数是曲线区间内的值。区间一般来说是递增区间,由曲线起点的区间最小值$t(0)$和曲线终点的区间最大值$t(1)$组成。
图43:计算曲线上参数到点为了创建一条NURBS曲线,通常来说需要提供如下信息:
- 维度,通常为3
- 阶数(有时候使用Order,等于阶数+1)
- 控制点列表
- 控制点权重列表
- 节点列表
创建曲线时,一般至少需要提供控制点的位置和阶数,其他的信息可以根据阶数和控制点列表自动生成。选择与起点重合的终点通常会创建一条闭合的周期曲线。下表是一些开放和封闭曲线的示例。
三阶闭合周期曲线 
移动非周期曲线的控制点并不能保证曲线的 
闭合钳位曲线的端点和控制点重合,周期曲线时平滑的闭合曲线,二者差异可以通过比较控制点和节点快速了解。
下面是一个开放的钳位非有理NURBS曲线的示例。该曲线有四个控制点,端点上有完全重复节点,且控制点权重均为1。
图44:分析三阶开放非有理NURBS曲线下面的圆形曲线(译者注:不是圆)是三阶闭合周期曲线的例子,他也是非有理即等权重的。注意周期曲线需要更多的控制点,并且有几个点重叠了。节点列表全部是单一节点。
图45:分析三阶闭合周期NURBS曲线注意周期曲线将四个控制点变成了七个(4+阶数)控制点,而钳位曲线仅仅使用四个控制点。周期曲线只使用单一节点,钳位曲线的端点使用完全重复节点,使曲线端点经过控制点。
如果我们将前面案例的阶数设置为二阶而不是3阶,那么节点列表长度会变小,并且周期曲线控制点数量会发生变化。
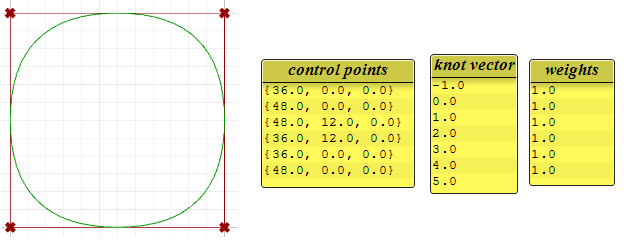
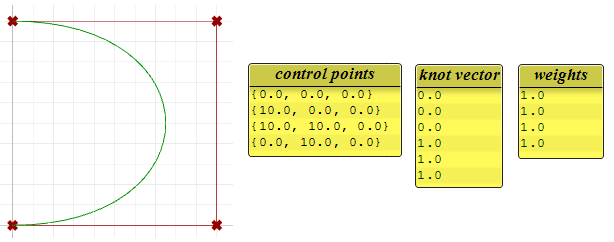
图46:分析二阶开放NURBS曲线 图47:分析二阶闭合周期NURBS曲线非有理均匀NURBS曲线的控制点权重均为1,但在有理曲线中可能会不一致,下面展示了权重变化的效果。
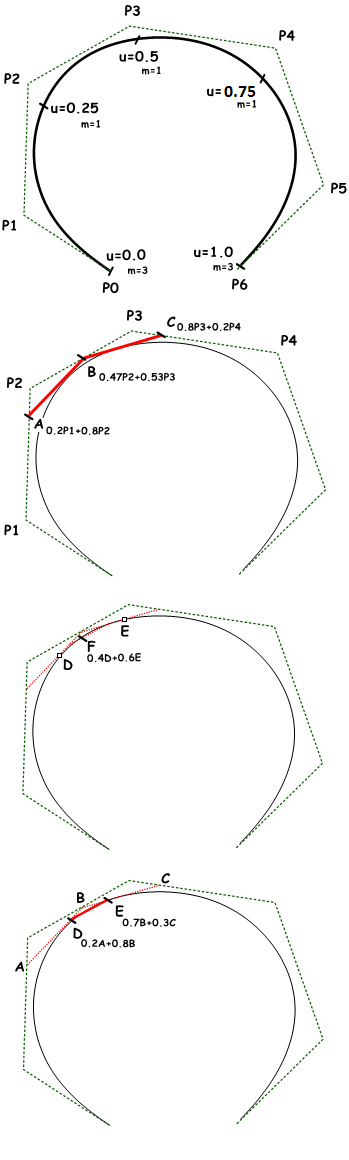
图48:分析开放NURBS曲线的权重 图49:分析闭合NURBS曲线的权重de Boor 算法以其发明者 Carl de Boor 命名,是 Bezier 曲线 de Casteljau 算法的推广。它具有数值稳定性,广泛用于评估 3D 应用中 NURBS 曲线上的点。以下是使用 de Boor 算法评估 3 阶 NURBS 曲线上的点的示例。
输入:
七个控制点$P0$到$P6$
节点列表:
输出:
曲线上$u=0.4$的点
解决步骤:
- 计算第一次迭代的系数
- 使用系数数据计算点:
- 计算第二次迭代的系数:
- 使用系数计算点:
- 计算最后一个系数
- 找到$u=0.4$参数处的点
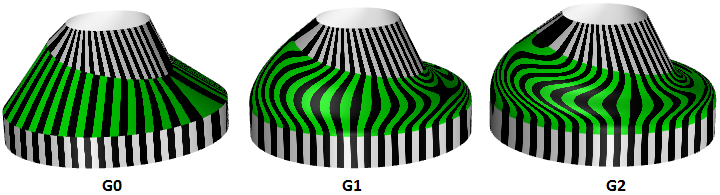
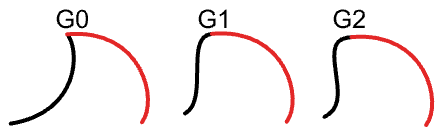
连续性是 3D 建模中的一个重要概念。连续性对于实现视觉平滑度以及获得平滑的光线反射和空气阻力非常重要。下表显示了各种连续性及其定义:
- G0(位置连续):两条曲线段仅连接在一起。
- G1(切向连续):两条曲线段在连接点处切向相同。
- G2(曲率连续):两条曲线段在连接点处的曲率和切向一致。
- GN:更高的连续性...
曲率是 3D 曲线和曲面建模中广泛使用的概念。曲率定义为单位弧长度上曲线切线的角度变化。对于圆或球体,它是半径的倒数,并且在整个区间中是恒定的。
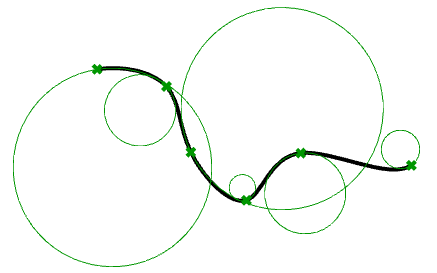
在平面中曲线上的任意一点,最接近通过的曲线该点的直线是切线。我们还可以找到经过该点并与曲线相切的最接近圆既曲率圆。该圆的半径的倒数就是该点的曲线曲率。
图51:检查不同点处的曲线曲率曲率圆可以位于曲线的左侧或右侧。如果我们关心这一点,我们会建立一个约定,例如如果圆位于曲线的左侧则给出曲率正号,如果圆位于曲线的右侧则给出负号。这称为有符号曲率。连接曲线的曲率值表示这些曲线之间的连续性。
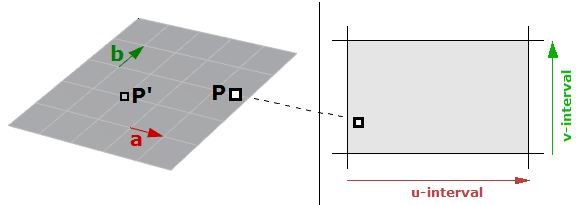
参数曲面是二维区间上有两个独立参数(通常表示为$u$和$v$)的函数。已平面为例,如果我们在平面上有一点$P$,并且平面上有两个不平行的向量$\mathbf{\vec a}$和$$\mathbf{\vec b}$$,那么我们可以用$u$和$v$定义平面的参数方程如下:
其中
另一个例子是球体。已原点为圆心半径位$R$的球体的笛卡尔方程为:
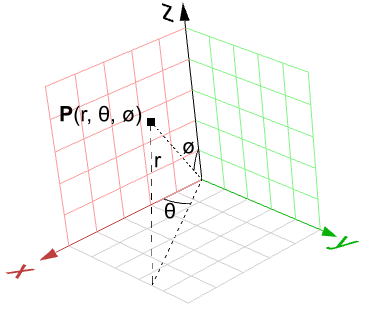
这意味着三个变量才能确定一个点,这对于需要两个变量的参数曲面来说没有意义。但在球面坐标系中,可以使用如下三个值进行球面上点的定位:
从球面坐标到笛卡尔坐标的点变换可通过如下公式计算:
其中:
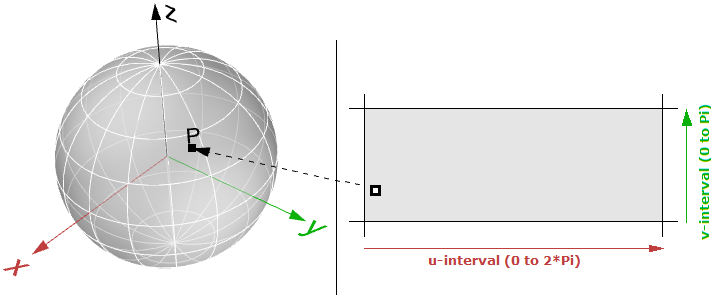
由于半径$r$是常数,所以我们只剩下两个变量,因此我们可用上述的变量来创建球面的参数表示:
即:
其中$(u,v)$在区间$(2\pi,\pi)$内
图54:球面的参数区间矩形平面参数曲面遵循如下的一般形式:
其中:
曲面区间被定义为表示能曲面上点的$(u,v)$参数范围。每个方向($u$或$v$)上参数的区间通常呗描述为两个值组成的一维区间($u_{min}$到$u_{max}$)和($v_{min}$到$v_{max}$)。
译者注:
区间一词出现在曲面时除非特殊说明是一维区间,默认均指二维区间。
更改曲面区间既重新参数化曲面。递增区间意味着区间的最小值表示曲面的最小点,和曲线相同,区间通常是递增的,但并非绝对。
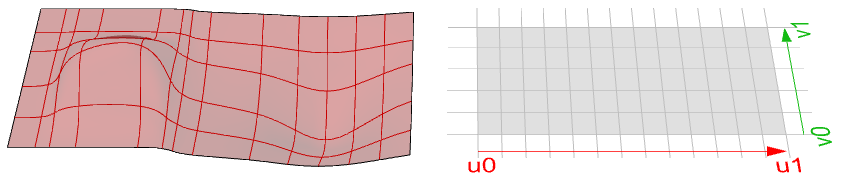
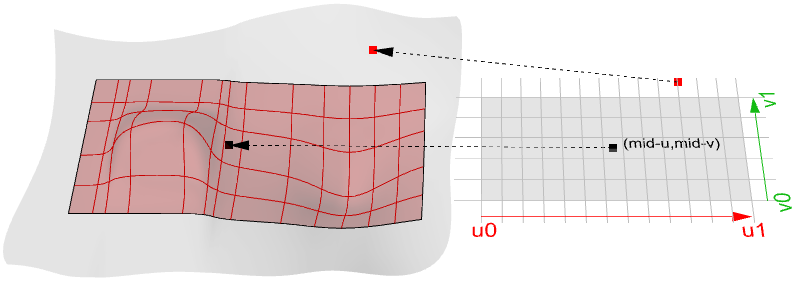
图55:3D空间中的NURBS曲面(左),曲面的参数区间矩形,区间在第一个方向上从u0到u1,第二个方向上从v0到v1(右)在曲面区间内的参数进行曲面计算会得到曲面上的点,同曲线一样曲面区间上的中心点不一定得到曲面的中心点。另外,曲面区间之外的u和v值不会得到有效的结果。
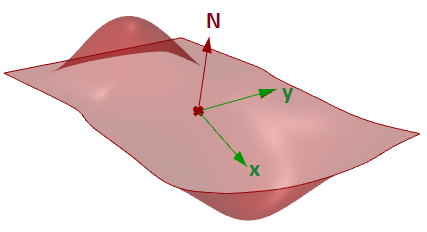
图56:曲面计算给定点处曲线的切平面是在该点整好接触曲面的平面,。切平面的z方向表示该点的法线方向。
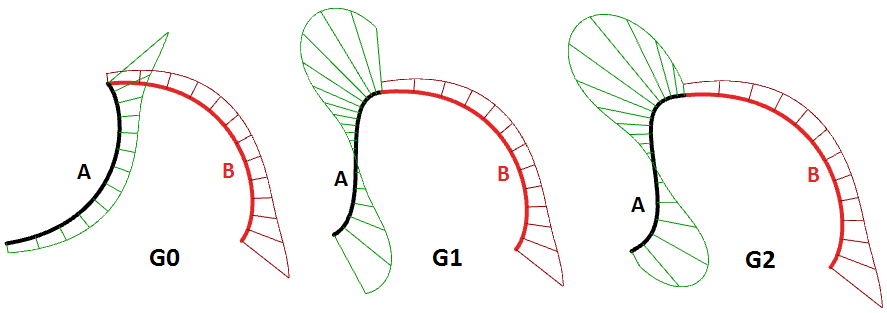
图57:曲线的切向量和法向量许多模型不能仅由一个曲面建好,曲面面片之间的连续性对于视觉上的平滑和光的反射以及空气阻力有重要意义。下面显示了各种连续性的定义。
- G0(位置连续):两个曲面仅连接在一起。
- G1(切向连续):两个曲面沿相接的边对应的切线在u和v方向均平行。
- G2(曲率连续):两条曲面在连接线处的曲率和切向一致。
- GN:更高的连续性...
对曲面来说,法向曲率是曲线曲率在曲面上的推广。给定曲面上一个点和该点切平面上一个方向,法向曲率的计算方法是将曲面和由该点和法向和一个自定义的方向构造的平面和曲面相交形成的交线在该点的有符号曲率。
如果我们取切平面上该点所有的方向,并计算对应的所有法向曲率,将有一个最大值和最小值。
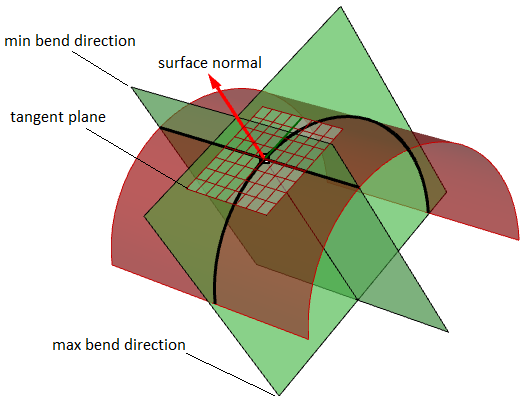
图59:法向曲率曲面上某点的主曲率是该点法向曲率的最大值和最小是,他表征了曲面上该点的最大和最小弯曲。用主曲率计算曲面的高斯曲率和平均曲率。
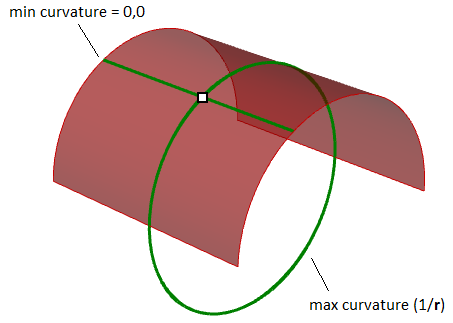
例如在圆柱面上,沿轴向方向没有弯曲(曲率为0),最大弯曲出现在平面和轴向垂直时(曲率等于半径的倒数)。这两个曲率(0和半径的倒数)构成了主曲率
图60:曲面上点的主曲率是该点的最大和最小曲率译者注:
光滑连续曲面某点的两个主曲率所在切割平面一定相互垂直。
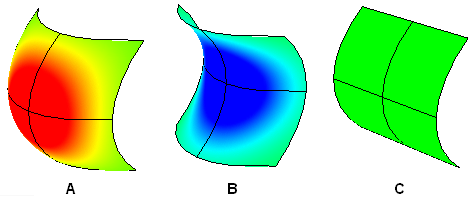
曲面上某点的高斯曲率是该点的两个主曲率的乘积。曲面上有正高斯曲率的点切平面仅经过该点,负高斯曲率的点切平面会切割表面。
A:碗状时高斯曲率为正。
B:马鞍状时高斯曲率为负。
C:当存在一个方向平坦时(圆柱、平面等),高斯曲率为0。
图61:分析曲面的高斯曲率曲面上某点的平均曲率是主曲率的平均值。平均曲率为0那么高斯曲率一定小于等于0。
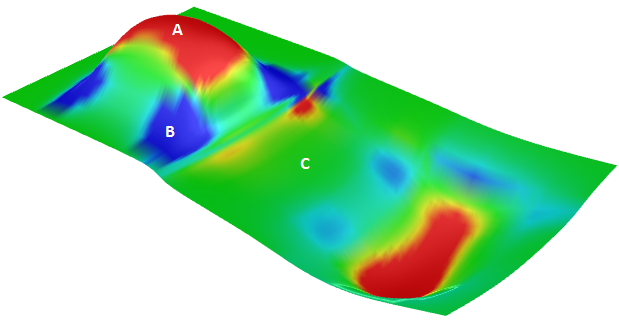
处处平均曲率均为0的曲面被称为极小曲面。在固定物体(如一个线环)上维持稳态的肥皂膜是一个典型的物理上的极小曲面。肥皂膜在稳态状态下两边气压相等,也没有形变,此时其面积也是最小化的。这与肥皂泡有极大区别,肥皂泡内部有空气,内外的压力并不一致。平均曲率可用于查找曲面曲率突变的区域。
处处平均曲率均相等的曲面被称为恒定曲率(CMC)曲面。CMC曲面包括稳态后的肥皂泡,附着在物体上或漂浮的泡泡均可。和肥皂膜不同,肥皂泡内有气体,内外压力形成了平衡,中间的压力差由肥皂泡膜面积最小化趋势产生的力平衡。
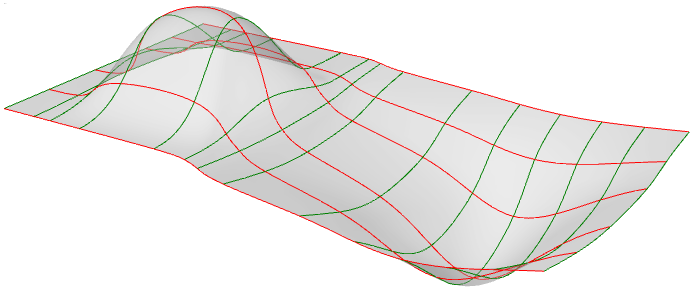
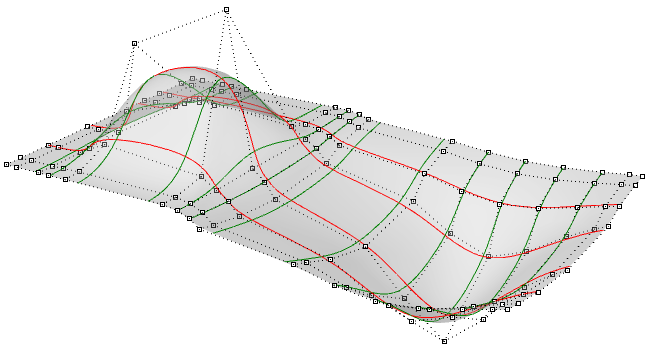
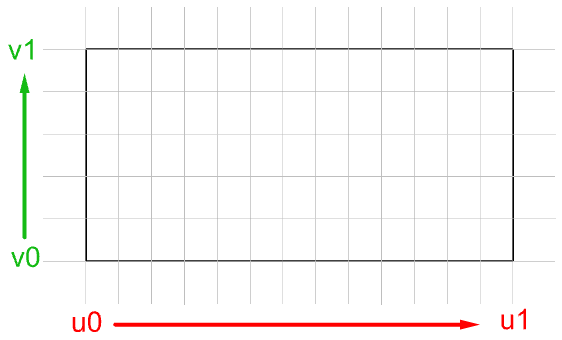
您可将NURBS曲面视为沿两个方向布置的NURBS曲线的网格。NURBS 曲面的形状由多个控制点以及该曲面在两个方向(u 和 v 方向)中每个方向上的阶数定义。NURBS 曲面可高效存储和表示高精度的自由曲面。NURBS 曲面的数学方程和细节超出了本文的范围。我们将只关注对设计师最有用的特性。
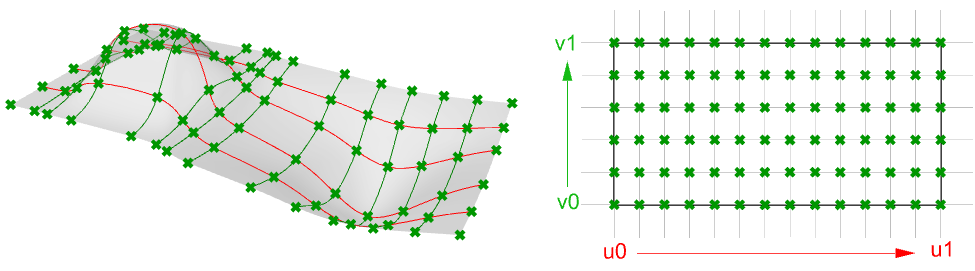
图62:NURBS曲面,u方向为红色等值线,v方向为绿色等值线 图63:NURBS曲面的控制结构 图64:NURBS曲面的参数区间矩形在大多数情况下,在参数区间矩形中相等间隔的参数不会转换为三维空间中的相等间隔。
图65:计算曲面上的点NURBS曲面的特性和NURBS曲线非常相似,只是增加了一个维度。NURBS曲面包含如下特性:
- 维度,通常为3
- u和v方向的阶数(有时候使用Order,等于阶数+1)
- 控制点列表
- 控制点权重列表
- 节点列表
和NURBS曲线一样,我们不需要了解如何创建NURBS曲面的具体细节,因为建模软件通常会提供一组包装好的工具。我们始终可以将曲面(以及关联的曲线)重建为新的控制点数和阶数。曲面同样可以是开放的、闭合的又或者是周期的。下面是一些示例。
译者注:下表中的闭合指一个方向的闭合而不是指曲面形成了封闭实体。
u方向阶数为3,v方向阶数为1的开放曲面。曲面角点控制点角点重合。
u方向阶数为3,v方向阶数为1的闭合(非周期的)曲面。控制点角点和曲面接缝重合。
u方向阶数为3,v方向阶数为1的闭合周期曲面。控制点和曲面接缝不重合。
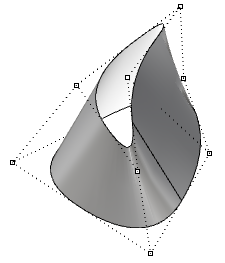
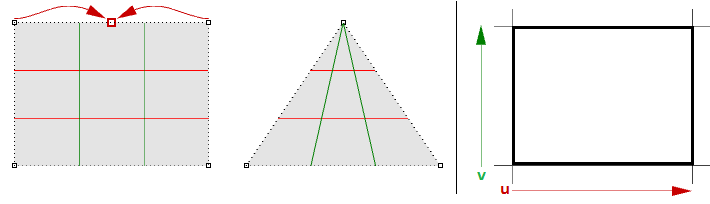
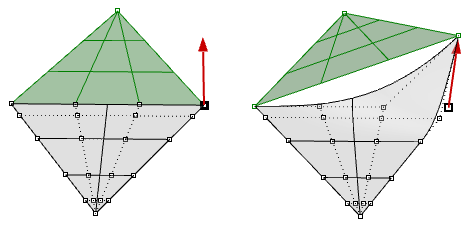
假如我们构造一个简单的一节矩形平面,拖动两个端点控制点到中间重叠,则获得了一个缩为单点的边。我们能注意到曲面的等值线在该点收敛。
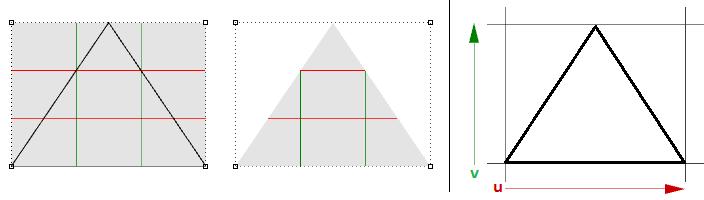
图66:折叠曲面的两个角点,创建有奇点的三角形,参数区间矩形没有变化上面的三角形也可以在不产生奇点的情况下构造,我们可以使用三角形线修剪曲面,当我们检查修剪曲面的底层NURBS结构时,我们会发现仍是矩形的。
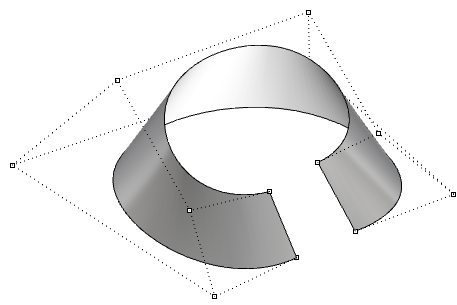
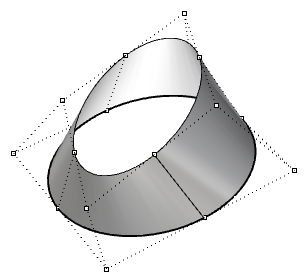
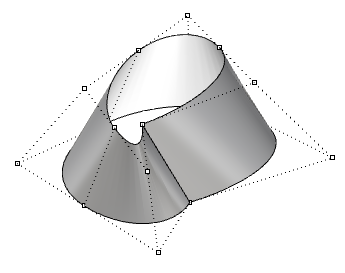
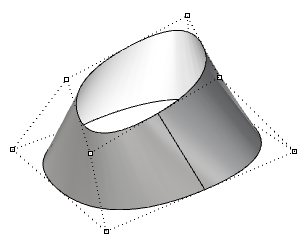
图67:修剪矩形NURBS曲面创建三角形面没有奇点就难以生成的曲面的其他常见例子是圆锥体和球体。圆锥体的顶部和球体的顶部和底部边缘折叠为一个点。无论是否存在奇点,参数区间矩形都或多或少地保持一个矩形区域。
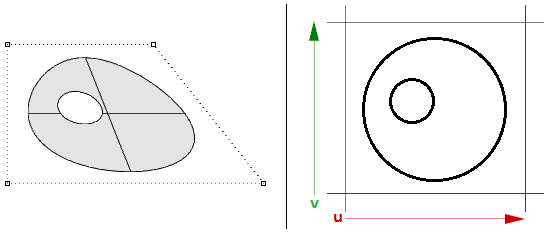
NURBS曲面可以修剪或取消修剪。修剪曲面使用基础NURBS曲面和闭合曲线来修剪该曲面的一部分。每个曲面都有一条闭合曲线用于定义外边界(外环),并且可以具有不相交的闭合内曲线来定义孔(内环)。具有与其底层 NURBS 曲面相同的外环且没有孔的曲面就是我们所说的未修剪曲面。
图68:模型空间里和参数区间中的修剪曲面一个多重曲面由两个或多个NURBS曲面(可能修剪过)组合组成。每个曲面都有自己的结构,参数区间,结构线方向等,并且多个曲面间无需一致。多重曲面使用边界表示法(BRep)表示。BRep结构描述了曲面、边缘、顶点以及他们的修剪和连接关系。修剪后的曲面也可由BRep数据结构组织。
图69:多重曲面有曲面组合而成,其公共边缘在公差范围内一致BRep是一种数据结构,它根据每个面的底层曲面、面的边缘、顶点、参数空间 2D 修剪以及每个相邻面之间的关系来描述多重曲面的数据结构。BRep对象在封闭(水密)时也称为实体。
如下图多重曲面是一个简单的立方体,由六个未修剪曲面连接在一起组成。
图70:由六个未修剪曲面连接在一起组成的多重曲面立方体也可以使用修剪的曲面组成相同的立方体,如下图中顶部的曲面。
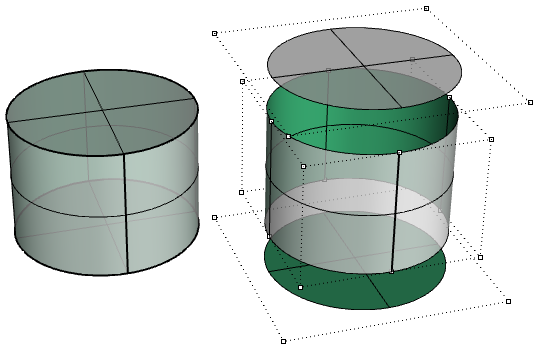
图71:可修建面组成的立方体下面示例中的圆柱体的顶面和底面是一个修剪的平面。
图72:底面上控制点的显示我们看到,编辑NURBS曲线和未修剪的曲面非常直观,并且可以通过移动控制点的方式交互完成。但是,编辑修剪曲面和多重曲面可能非常难。主要挑战是能够将不同面的连接边缘保持在所需的公差范围内。共享公共边的相邻面可以进行修剪,并且通常不具有匹配的 NURBS 结构,因此以使该公共边变形的方式修改对象可能会导致间隙。
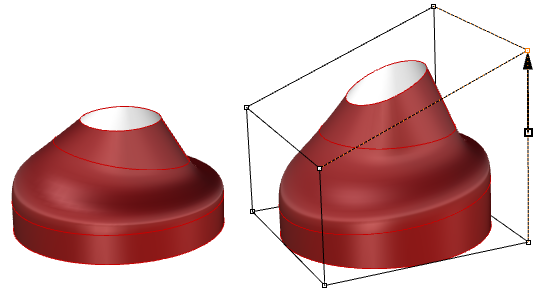
图73:两个三角形面连接在一个多重曲面中,但没有匹配的连接边。移动一个角会创建一个孔另一个挑战是,通常较难直接控制结果,尤其是在修改修剪几何图形时。
图74:创建修剪曲面后,对编辑结果控制有限 图75:使用变形盒编辑多重曲面在参数区间矩形中,使用未修剪的底层曲面与二维修剪曲线相结合来描述修剪曲面,这些曲线的计算结果为三维曲面内的三维边。
以下案例使用本章中学习的概念。他们使用 Rhinoceros 5 和 Grasshopper 0.9创建。
译者注:
经测试教程中的案例在Rhino8和GH1中正常运行,暂无精力将教案中所有代码更新到Rhino8新增的ScriptEditer中。
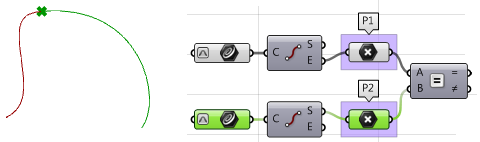
检查两条输入曲线之间的连续性。假定曲线在第一条曲线的末端和第二条曲线的起点相交。
输入:
两条曲线
参数:
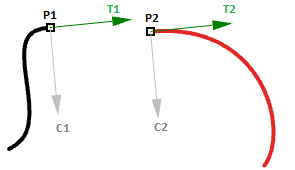
- 第一条曲线的终点P1
- 第二条曲线的起点P2
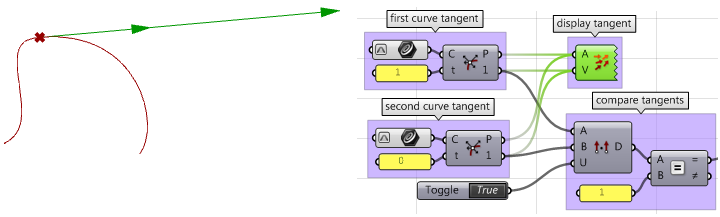
- 第一条曲线末端和第二条曲线起点处的切线:T1和T2
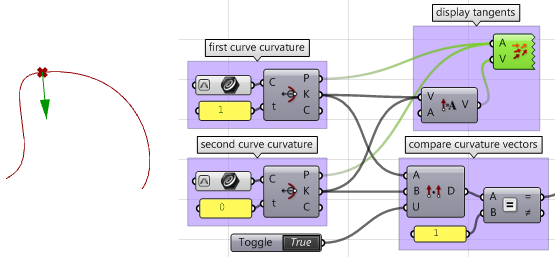
- 第一条曲线末端和第二条曲线起点处的曲率:C1和C2
解决方案:
-
重新参数化输入曲线。我们这样做是为了我们知道曲线的起点在$t=0$计算,终点在$t=1$计算。
-
提取两条曲线的终点和起点,并检查它们是否重合。如果是,两条曲线至少是G0连续。
-
计算切向量
-
使用点积比较切线,确定做了向量单位化操作。如果向量平行,那么我们有G1连续。
-
计算曲率向量(法向)
-
比较曲率向量,如果二者一致,则两曲线G2连续。
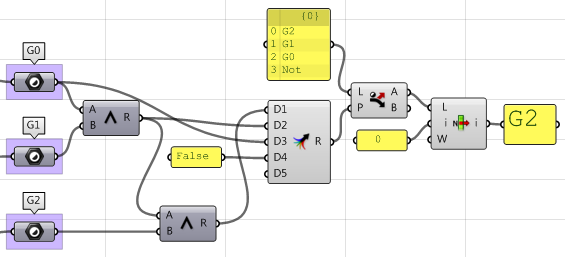
-
创建筛选三个结果(G1、G2 和 G3)的逻辑,并选择最高的连续性。
使用VB组件:
Private Sub RunScript(ByVal c1 As Curve, ByVal c2 As Curve, ByRef A As Object)
'定义变量
Dim continuity As New String("")
Dim t1, t2 As Double
Dim v_c1, v_c2, c_c1, c_c2 As Vector3d
'得到起点终点
Dim end_c1 = c1.PointAtEnd
Dim start_c2 = c2.PointAtStart
'G0连续检查
If end_c1.DistanceTo(start_c2) = 0 Then
continuity = "G0"
End If
'G1连续检查
If continuity = "G0" Then
'计算切向
v_c1 = c1.TangentAtEnd
v_c2 = c2.TangentAtStart
'单位化向量
v_c1.Unitize
v_c2.Unitize
'比较向量
If v_c1 * v_c2 = 1.0 Then
continuity = "G1"
End If
End If
'G2连续检查
If continuity = "G1" Then
'获得曲线区间最值
t1 = c1.Domain.Max
t2 = c2.Domain.Min
'计算曲率向量
c_c1 = c1.CurvatureAt(t1)
c_c2 = c2.CurvatureAt(t2)
'单位化
c_c1.Unitize
c_c2.Unitize
'向量比较
If c_c1 * c_c2 = 1.0 Then
continuity = "G2"
End If
End If
'结果输出
A = continuity
End Sub使用Python组件:
#定义变量
continuity = ""
#得到起点终点
end_c1 = c1.PointAtEnd
start_c2 = c2.PointAtStart
#G0连续检查
if end_c1.DistanceTo(start_c2) == 0:
continuity = "G0"
#G1连续检查
if continuity == "G0":
#计算切向
v_c1 = c1.TangentAtEnd
v_c2 = c2.TangentAtStart
#单位化向量
v_c1.Unitize()
v_c2.Unitize()
#比较向量
dot = v_c1 * v_c2
if dot == 1.0:
continuity = "G1"
else:
print("Failed G1")
print(dot)
#G2连续检查
if continuity == "G1":
#获得曲线区间最值
t1 = c1.Domain.Max
t2 = c2.Domain.Min
#计算曲率向量
c_c1 = c1.CurvatureAt(t1)
c_c2 = c2.CurvatureAt(t2)
#单位化
c_c1.Unitize()
c_c2.Unitize()
#向量比较
dot = c_c1 * c_c2
if dot == 1.0:
continuity = "G2"
else:
print("Failed G2")
print(dot)
#输出结果
A = continuity使用c#组件:
private void RunScript(Curve c1, Curve c2, ref object A)
{
//定义变量
string continuity = ("");
double t1, t2;
Vector3d v_c1, v_c2, c_c1, c_c2;
//得到起点终点
Point3d end_c1 = c1.PointAtEnd;
Point3d start_c2 = c2.PointAtStart;
//G0连续检查
if( end_c1.DistanceTo(start_c2) == 0){
continuity = "G0";
}
//G1连续检查
if( continuity == "G0")
{
//计算切向
v_c1 = c1.TangentAtEnd;
v_c2 = c2.TangentAtStart;
//单位化向量
v_c1.Unitize();
v_c2.Unitize();
//比较向量
if( v_c1 * v_c2 == 1.0 ){
continuity = "G1";
}
}
//G2连续检查
if( continuity == "G1" )
{
//获得曲线区间最值
t1 = c1.Domain.Max;
t2 = c2.Domain.Min;
//计算曲率向量
c_c1 = c1.CurvatureAt(t1);
c_c2 = c2.CurvatureAt(t2);
//单位化
c_c1.Unitize();
c_c2.Unitize();
//向量比较
if( c_c1 * c_c2 == 1.0 ){
continuity = "G2";
}
}
//输出结果
A = continuity;
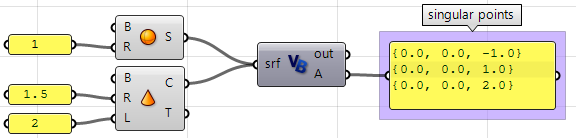
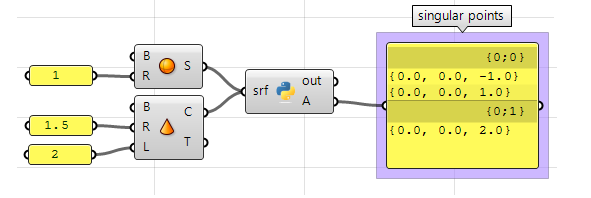
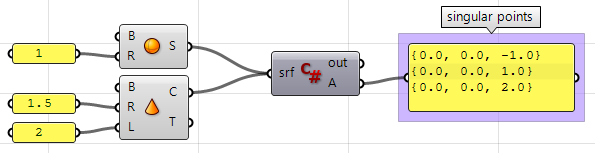
}提取球体和圆锥中的奇点。
输入:
参数:
奇点可通过分析具有无效或0长度修剪边来检测。
解决方案:
- 遍历所有边缘。
- 检查是否有无效修剪边缘并标记。
- 提取在空间中该点的位置。
使用VB组件:
Private Sub RunScript(ByVal srf As Brep, ByRef A As Object)
'定义点列表
Dim singular_points As New List( Of Point3d)
'获得所有BRep边缘
For Each trim As BrepTrim In srf.Trims
'标记为空的边缘
If trim.Edge Is Nothing Then
'找到对应参数区间的位置
Dim pt2d = New Point2d(trim.PointAtStart)
'计算模型空间中位置
Dim pt3d = trim.Face.PointAt(pt2d.x, pt2d.y)
'添加到结果列表
singular_points.Add(pt3d)
End If
Next
'输出
A = singular_points
End Sub
使用python组件:
#定义点列表
singular_points = []
#获得所有BRep边缘
for trim in srf.Trims:
#标记为空的边缘
if trim.Edge == None:
#找到对应参数区间的位置
pt2d = trim.PointAtStart
#计算模型空间中位置
pt3d = trim.Face.PointAt(pt2d.X, pt2d.Y)
#添加到结果列表
singular_points.append(pt3d)
#输出
A = singular_points使用c#组件:
private void RunScript(Brep srf, ref object A)
{
//定义点列表
List < Point3d > singular_points = new List<Point3d>();
//获得所有BRep边缘
foreach( BrepTrim trim in srf.Trims)
{
//标记为空的边缘
if( trim.Edge == null)
{
//找到对应参数区间的位置
Point2d pt2d = new Point2d(trim.PointAtStart);
//计算模型空间中位置
Point3d pt3d = trim.Face.PointAt(pt2d.X, pt2d.Y);
//添加到结果列表
singular_points.Add(pt3d);
}
}
//输出
A = singular_points
}- Edward Angel, “InteractiveComputer Graphics with OpenGL,” Addison Wesley Longman, Inc., 2000.
- James D Foley, Steven K Feiner, John FHughes, “Introduction to Computer Graphics” Addison-WesleyPublishing Company, Inc., 1997.
- James Stewart, “Calculus,“Wadsworth, Inc., 1991.
- Kenneth Hoffman, Ray Kunze, “LinearAlgebra”, Prentice-Hall, Inc., 1971
- Rhinoceros® help document, RobertMcNeel and Associates, 2009.
Footnotes