README.md

63. 不同路径 II

English Version

题目描述

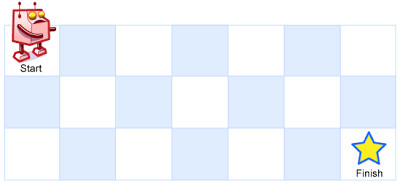
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

 

示例 1：

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

示例 2：

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

 

提示：

• m == obstacleGrid.length
• n == obstacleGrid[i].length
• 1 <= m, n <= 100
• obstacleGrid[i][j] 为 0 或 1

解法

Go

func uniquePathsWithObstacles(obstacleGrid [][]int) int {
    m,n := len(obstacleGrid),len(obstacleGrid[0])
    dp := make([][]int,m)
    for i:=0; i < m;i++ {
        dp[i] = make([]int,n)
    }
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if obstacleGrid[i][j] == 0 {
                if i == 0 && j == 0 {
                    dp[i][j] = 1
                } else if i > 0 && j >0 {
                    dp[i][j] = dp[i][j-1]+dp[i-1][j]
                } else if i > 0 {
                    dp[i][j] = dp[i-1][j]
                } else {
                    dp[i][j] = dp[i][j-1]
                }
            }
        }
    }
    return dp[m-1][n-1]
}


<!-- tabs:start -->

### **Python3**
<!-- 这里可写当前语言的特殊实现逻辑 -->

```python

Java

...