README.md

74. 搜索二维矩阵

English Version

题目描述

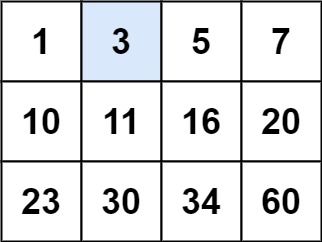
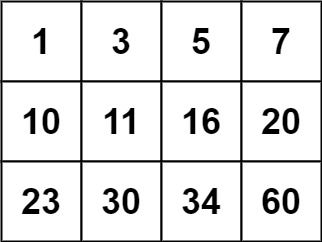
编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

• 每行中的整数从左到右按升序排列。
• 每行的第一个整数大于前一行的最后一个整数。

 

示例 1：

输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

示例 2：

输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

 

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -104 <= matrix[i][j], target <= 104

解法

将二维矩阵逻辑展开，然后二分查找即可。

Python3

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        m, n = len(matrix), len(matrix[0])
        l, h = 0, m * n - 1
        while l <= h:
            mid = (l + h) >> 1
            x, y = divmod(mid, n)
            if matrix[x][y] == target:
                return True
            if matrix[x][y] < target:
                l = mid + 1
            else:
                h = mid - 1
        return False

Java

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length, n = matrix[0].length;
        int l = 0, h = m * n - 1;
        while (l <= h) {
            int mid = (l + h) >>> 1;
            int x = mid / n, y = mid % n;
            if (matrix[x][y] == target) return true;
            if (matrix[x][y] < target) l = mid + 1;
            else h = mid - 1;
        }
        return false;
    }
}

C++

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size();
        int l = 0, h = m * n - 1;
        while (l <= h) {
            int mid = l + ((h - l) >> 1);
            int x = mid / n, y = mid % n;
            if (matrix[x][y] == target) return true;
            if (matrix[x][y] < target) l = mid + 1;
            else h = mid - 1;
        }
        return false;
    }
};

JavaScript

/**
 * @param {number[][]} matrix
 * @param {number} target
 * @return {boolean}
 */
var searchMatrix = function (matrix, target) {
  const m = matrix.length;
  const n = matrix[0].length;
  let l = 0;
  let h = m * n - 1;
  while (l <= h) {
    const mid = (l + h) >>> 1;
    const x = Math.floor(mid / n);
    const y = mid % n;
    if (matrix[x][y] == target) {
      return true;
    }
    if (matrix[x][y] < target) {
      l = mid + 1;
    } else {
      h = mid - 1;
    }
  }
  return false;
};

...