By Endermanch and WitherOrNot
We need to use a random Raw Product Key as a base to generate a Product ID in a form of AAAAA-BBB-CCCCCCS-DDEEE.
| Digits | Meaning |
|---|---|
| AAAAA | OS Family constant |
| BBB | Channel ID |
| CCCCCC | Sequence Number |
| S | Check digit |
| DD | Public key index |
| EEE | Random 3-digit number |
The OS Family constant AAAAA is different for each series of Windows XP. For example, it is 76487 for SP3.
The BBB and CCCCCC sections essentially encode the Raw Product Key. For example, if the first section is equal to XXX and the second section is equal to YYYYYY, the Raw Product Key will be encoded as XXX-YYYYYY.
The check digit S is picked so that the sum of all C digits with it added makes a number divisible by 7.
The public key index DD lets us know which public key was used to successfully verify the authenticity of our Product Key.
For example, it's 22 for Professional keys and 23 for VLK keys. This value is equal to half of the BINK ID (discussed below).
A random number EEE is used to generate a different Installation ID each time.
The Product Key itself (not to confuse with the RPK) is in form FFFFF-GGGGG-HHHHH-JJJJJ-KKKKK, encoded in Base-24 with
the alphabet BCDFGHJKMPQRTVWXY2346789 to exclude any characters that can be easily confused, like I and 1 or O and 0.
As per the alphabet capacity formula, the key can at most contain 114 bits of information.
Based on that calculation, we unpack the 114-bit Product Key into 4 ordered segments:
| Segment | Capacity | Data |
|---|---|---|
| Upgrade | 1 bit | Upgrade version flag |
| Serial | 30 bits | Raw Product Key (RPK) |
| Hash | 28 bits | RPK hash |
| Signature | 55 bits | Elliptic Curve signature for the RPK hash |
For simplicity' sake, we'll combine Upgrade and Serial segments into a single segment called Data. By that logic we'll be able to extract the RPK by
shifting Data right and pack it back by shifting bits left, because most a priori valid product keys I've checked had the Upgrade bit set to 1.
Microsoft redid their Product Key format with Windows Server 2003 to include a backend server authentication key, which was an actually secure approach to license validation, as no one could ever make a guess on which validation algorithm they had employed on their private server. Besides adding the online validation mechanism, they also cranked up the overall arithmetic from 384 to 512 bits, and the signature scalar to 62 bits of information.
| Segment | Capacity | Data |
|---|---|---|
| Upgrade | 1 bit | Upgrade version flag |
| Channel ID | 10 bits | The BBB part of the RPK |
| Hash | 31 bits | RPK hash |
| Signature | 62 bits | Elliptic Curve signature for the RPK hash |
| Auth Key | 10 bits | Backend authentication value |
However, if we generated a key without the online activation in mind, we still could generate valid keys that would let us through the setup of the operating system. And that's exactly what the code does - it generates a random 10-bit authentication key. Nowadays it doesn't matter at all, as activation servers are down and Server 2003 is considered abandonware, the same way this entire project shouldn't be considered piracy.
Elliptic Curve Cryptography (ECC) is a type of public-key cryptographic system. This class of systems relies on challenging "one-way" math problems - easy to compute one way and intractable to solve the "other" way. Sometimes these are called "trapdoor" functions - easy to fall into, complicated to escape.[5]
ECC relies on solving equations of the form
In general, there are 2 special cases for the Elliptic Curve leveraged in cryptography - F2m and Fp.
They differ only slightly. Both curves are defined over the finite field, Fp uses a prime parameter that's larger than 3,
F2m assumes
An elliptic curve over the finite field Fp consists of:
- a set of integer coordinates
${x, y}$ , such that$0 \le x, y < p$ ; - a set of points
$y^2 = x^3 + ax + b \mod p$ .
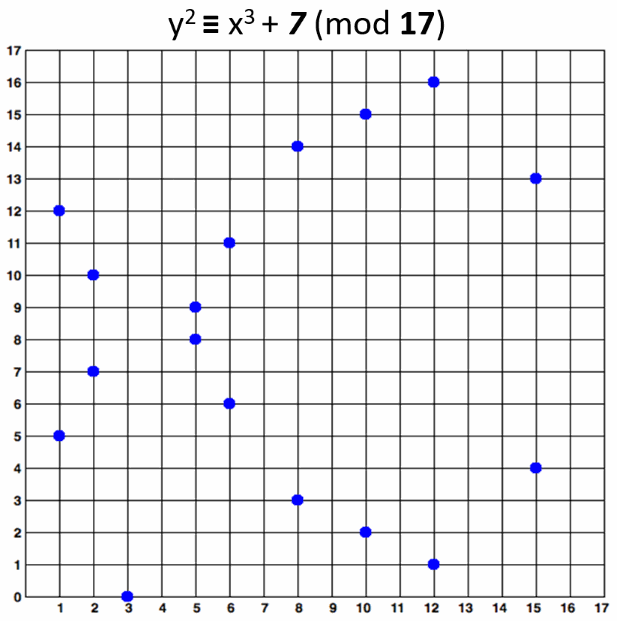
An elliptic curve over F17 would look like this:
The curve consists of the blue points in above image. In practice the "elliptic curves" used in cryptography are "sets of points in a square matrix".
The above curve is "educational". It provides very small key length (4-5 bits). In real world situations developers typically use curves of 256-bits or more.
An important concept is that addition can be defined between two points on an elliptic curve. This also allows a definition of integer multiplication (
The core of elliptic curve cryptography uses this multiplication definition, as solving the equation
Since it is a public-key cryptographic system, Microsoft had to share the public key with their Windows XP release to check entered product keys against.
It is stored within pidgen.dll in a form of a BINK resource. The first set of BINK data is there to validate retail keys, the second is for the
OEM keys respectively.
The structure of the BINK resource for Windows 98 and Windows XP is as follows:
| Offset | Value |
|---|---|
0x0000 |
BINK ID |
0x0004 |
Size of BINKEY structure in bytes (always 0x16C in practice) |
0x0008 |
Header length (always 7 in practice) |
0x000C |
Checksum |
0x0010 |
Number-encoded date - BINKEY version (always 19980206 in practice) |
0x0014 |
ECC curve order size (always 12 in practice) |
0x0018 |
Hash length (always 28 in practice) |
0x001C |
Signature length (always 55 in practice) |
0x0020 |
Finite Field Order p |
0x005C |
Curve Parameter a |
0x0098 |
Curve Parameter b |
0x00D4 |
Base Point x-coordinate Gx |
0x0110 |
Base Point y-coordinate Gy |
0x014C |
Public Key x-coordinate Kx |
0x0188 |
Public Key y-coordinate Ky |
Each segment is marked with a different color, the BINK header values are the same.
Windows Server 2003 and Windows XP x64 implement it differently:
| Offset | Value |
|---|---|
0x0000 |
BINK ID |
0x0004 |
Size of BINKEY structure in bytes |
0x0008 |
Header length (always 9 in practice) |
0x000C |
Checksum |
0x0010 |
Number-encoded date - BINKEY version (always 20020420 in practice) |
0x0014 |
ECC curve order size (always 16 in practice) |
0x0018 |
Hash length (always 31 in practice) |
0x001C |
Signature length (always 62 in practice) |
0x0020 |
Backend authentication value length (always 12 in practice) |
0x0024 |
Product ID length (always 20 in practice) |
0x0028 |
Finite Field Order p |
0x0068 |
Curve Parameter a |
0x00A8 |
Curve Parameter b |
0x00E8 |
Base Point x-coordinate Gx |
0x0128 |
Base Point y-coordinate Gy |
0x0168 |
Public Key x-coordinate Kx |
0x01A8 |
Public Key y-coordinate Ky |
And here are my structure prototypes made for the BINK Reader in C:
typedef struct _EC_BYTE_POINT {
CHAR x[256]; // x-coordinate of the point on the elliptic curve.
CHAR y[256]; // y-coordinate of the point on the elliptic curve.
} EC_BYTE_POINT;
typedef struct _BINKHDR {
// BINK version - not stored in the resource.
ULONG32 dwVersion;
// Original BINK header.
ULONG32 dwID;
ULONG32 dwSize;
ULONG32 dwHeaderLength;
ULONG32 dwChecksum;
ULONG32 dwDate;
ULONG32 dwKeySizeInDWORDs;
ULONG32 dwHashLength;
ULONG32 dwSignatureLength;
// Extended BINK header. (Windows Server 2003+)
ULONG32 dwAuthCodeLength;
ULONG32 dwProductIDLength;
} BINKHDR;
typedef struct _BINKDATA {
CHAR p[256]; // Finite Field order p.
CHAR a[256]; // Elliptic Curve parameter a.
CHAR b[256]; // Elliptic Curve parameter b.
EC_BYTE_POINT G; // Base point (Generator) G.
EC_BYTE_POINT K; // Public key K.
} BINKDATA;
typedef struct _BINKEY {
BINKHDR header;
BINKDATA data;
} BINKEY;Please note throughout this section that whenever integers are converted to bytes or vice-versa, they are in little-endian byte order.
First, let's define some variables used in these algorithms:
-
$m$ , theDatasection of the product key (Raw Product Key/Channel ID and Upgrade bit) -
$h$ , theHashsection of the product key -
$s$ , theSignaturesection of the product key -
$k$ , the private key, used to generate product keys -
$a$ , theAuthentication Infosection of the product key (BINK2002 only)
The constant
- Using base-24 conversion, with the base alphabet
BCDFGHJKMPQRTVWXY2346789, convert the product key into an integer - From this integer, extract the values
$m$ ,$h$ , and$s$ using bit-shifting and logical ANDs - Compute the elliptic curve point
$R = hK + sG$ - Compute
digest = SHA1(m || R.x || R.y), where||represents byte concatenation - Convert
digestto an integer - Let
$h_t$ be the lower 28 bits ofdigest - Compare
$h$ and$h_t$ , if they are equal, the product key is valid
- Compute a random number
$c$ - Compute the random point
$R = cG$ - Compute
digest = SHA1(m || R.x || R.y) - Let
$h$ be integer formed by the lower 28 bits ofdigest - Let
$s = kh + c \pmod{p}$ - Pack
$s$ ,$h$ , and$m$ into a 114-bit integer - Convert this integer into a product key, using base-24 conversion
The point
The values
- Using base-24 conversion, with the base alphabet
BCDFGHJKMPQRTVWXY2346789, convert the product key into an integer - From this integer, extract the values
$m$ ,$h$ , and$s$ using bit-shifting and logical ANDs - Compute
digest1 = SHA1(5D || m || h || a || 00 00) - Let
$e$ be the integer formed by the lower 62 bits ofdigest1 - Let
$R = s(sG + eK)$ - Let
digest2 = SHA1(79 || m || R.x || R.y) - Let
$h_t$ be the lower 31 bits ofdigest2 - Compare
$h$ and$h_t$ , if they are equal, the product key is valid
Afterwards, the value
- Compute a random number
$c$ - Compute the random point
$R = cG$ - Let
digest2 = SHA1(79 || m || R.x || R.y) - Let
$h$ be integer formed by the lower 31 bits ofdigest2 - Compute
digest1 = SHA1(5D || m || h || a || 00 00) - Let
$e$ be the integer formed by the lower 62 bits ofdigest1 - Let
$s = \frac{-ek + \sqrt{\left(ek\right)^2 + 4c}}{2} \pmod {n}$ - Compute
$a$ by unknown algorithm - Pack
$s$ ,$h$ , and$m$ , and$a$ into a 114-bit integer - Convert this integer into a product key, using base-24 conversion
The variables used in this algorithm are related as follows:
During generation,
If we want to generate valid product keys for Windows XP, we must compute the corresponding private key using the public key supplied with pidgen.dll,
which means we have to reverse-solve the one-way ECC task.
Judging by the key located in BINK, the curve order is 384 bits long in Windows XP and 512 bits long in Server 2003 / XP x64 respectively.
The computation difficulty using the most efficient Pollard's Rho algorithm with asymptotic complexity
As mentioned before, there's only one public tool that satisfies our current needs, which is the ECDLP solver by Mr. HAANDI.
To compute the private key, we will need to supply the tool with the public ECC values located in the BINK resource, as well as the order genOrder of the base point G(Gx; Gy).
The order of the base point can be computed using SageMath.
Here's the basic algorithm I used to reverse the Windows 98 private key:
- Compute the order of the base point using SageMath. In SageMath, execute the following commands:
E = EllipticCurve(GF(p), [0, 0, 0, a, b]), wherep,aandbare decimally represented elliptic curve parameters from the BINK resource.G = E(Gx, Gy), whereGxandGyare decimally represented base point coordinates from the BINK resource.K = E(Kx, Ky), whereKxandKyare decimally represented public key coordinates from the BINK resource.n = G.order(),nwill be the computed order of the base point. It may take some time to compute, even on the newest builds.- Factor the order using
factor(n). Microsoft used prime numbers for the point orders, so if it returns the number itself, it's completely normal. - Save the resulting factors of the order somewhere.
-Kwill give you the inverse of the public key in a projective plane with coordinates(x : y : z). Save theycoordinate somewhere, it is required to generate a correct private key.
- Compute the private key using ECDLP Solver v0.2a.
- The tool comes with a template job
job_template.txtand a ReadMe file. It's necessary to understand how the tool works to use it. - Insert all public elliptic curve values from the BINK resource, except the
Kycoordinate. To generate a correct private key, you must use the inverse coordinate-Kyyou have calculated in SageMath earlier. - Insert the factors of the base point order
nand specify the factor count. It will very likely be1, as Microsoft mainly uses primes for their generator orders. - Run the tool
<arch> ECDLP Solver.exe <job_name>.txtand wait until it calculates the private keyk = %dfor you.
- The tool comes with a template job
Here's an example of the Windows XP job job_xp.txt that yields the correct private key for the ECDLP Solver.
GF := GF(22604814143135632990679956684344311209819952803216271952472204855524756275151440456421260165232069708317717961315241);
E := EllipticCurve([GF|1,0]);
G := E![10910744922206512781156913169071750153028386884676208947062808346072531411270489432930252839559606812441712224597826,19170993669917204517491618000619818679152109690172641868349612889930480365274675096509477191800826190959228181870174];
K := E![14399230353963643339712940015954061581064239835926823517419716769613937039346822269422480779920783799484349086780408,17120082747148185997450361756610881166187863099877353630300913555824935802439591336620545428308962346299700128114607];
/*
FactorCount:=1;
61760995553426173
*/And the ECDLP Solver output for it:
In Windows versions before XP, the channel ID is rarely validated except in certain products, such as Windows 98 SE Select Edition. In Windows XP and Server 2003, however, the channel ID is validated to determine the license type for a specific copy. This validation is done by DPCDLL.DLL, which contains a table of signed channel ID ranges and their associated license type.
For all NT 5 Windows versions except Server 2003 R2, this table has the following structure for each row:
| Offset | Value |
|---|---|
0x0000 |
Index |
0x0004 |
BINK ID |
0x0008 |
Minimum Channel ID |
0x000C |
Maximum Channel ID |
0x0010 |
License Type |
0x0014 |
Activation Grace Period (in days) |
0x0018 |
Evaluation Period (in days) |
0x001C |
Signature Length |
0x0020 |
Signature |
The license types are as follows:
| Type | Meaning |
|---|---|
| 1 | Volume (VLK) |
| 2 | Retail/OEM Certificate of Authenticity (OEM-COA) |
| 3 | Evaluation |
| 4 | Tablet |
| 5 | OEM System Locked Pre-Installation (OEM-SLP) |
| 6 | Embedded |
For the Evaluation Period and Activation Grace Period values, the value 2147483647 is used to indicate N/A.
When a key with an invalid channel ID and correct BINK is supplied during setup, the setup installed will accept the key since it has a valid signature. However, when attempting to login to the system, the system will prevent login until the system is activated. When attempting to activate, a non-functional OOBE Activation popup will appear, blocking login and effectively bricking the system, as shown below.
This strange behavior is most likely a bug triggered by a lack of error handling in DPCDLL's channel ID validation code.
I will add more decent reads into the bibliography in later releases.
Understanding basics of Windows XP Activation:
- [1] Inside Windows Product Activation - Fully Licensed
- [2] MSKey 4-in-1 ReadMe
- [3] Windows序列号产生原理(椭圆曲线法)
Understanding Elliptic Curve Cryptography:
- [4] Elliptic Curve Cryptography for Beginners - Matt Rickard
- [5] Elliptic Curve Cryptography (ECC) - Practical Cryptography for Developers
- [6] A (Relatively Easy To Understand) Primer on Elliptic Curve Cryptography - Cloudflare
Public discussions: