Skip to content

Latest commit

 

History

History
354 lines (302 loc) · 9.39 KB

README_EN.md

File metadata and controls

354 lines (302 loc) · 9.39 KB
comments difficulty edit_url tags
true
Hard
Tree
Depth-First Search
Dynamic Programming
Binary Tree

124. Binary Tree Maximum Path Sum

中文文档

Description

A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.

The path sum of a path is the sum of the node's values in the path.

Given the root of a binary tree, return the maximum path sum of any non-empty path.

 

Example 1:

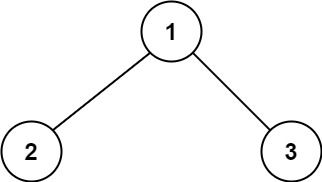
Input: root = [1,2,3]
Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.

Example 2:

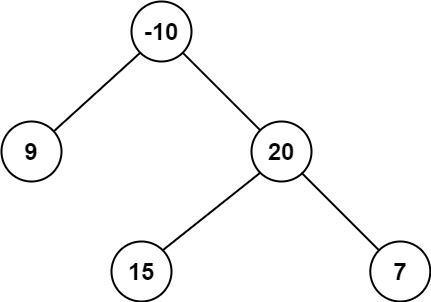
Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

 

Constraints:

  • The number of nodes in the tree is in the range [1, 3 * 104].
  • -1000 <= Node.val <= 1000

Solutions

Solution 1: Recursion

When thinking about the classic routine of recursion problems in binary trees, we consider:

  1. Termination condition (when to terminate recursion)
  2. Recursively process the left and right subtrees
  3. Merge the calculation results of the left and right subtrees

For this problem, we design a function $dfs(root)$, which returns the maximum path sum of the binary tree with $root$ as the root node.

The execution logic of the function $dfs(root)$ is as follows:

If $root$ does not exist, then $dfs(root)$ returns $0$;

Otherwise, we recursively calculate the maximum path sum of the left and right subtrees of $root$, denoted as $left$ and $right$. If $left$ is less than $0$, then we set it to $0$, similarly, if $right$ is less than $0$, then we set it to $0$.

Then, we update the answer with $root.val + left + right$. Finally, the function returns $root.val + \max(left, right)$.

In the main function, we call $dfs(root)$ to get the maximum path sum of each node, and the maximum value among them is the answer.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes in the binary tree.

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxPathSum(self, root: Optional[TreeNode]) -> int:
        def dfs(root: Optional[TreeNode]) -> int:
            if root is None:
                return 0
            left = max(0, dfs(root.left))
            right = max(0, dfs(root.right))
            nonlocal ans
            ans = max(ans, root.val + left + right)
            return root.val + max(left, right)

        ans = -inf
        dfs(root)
        return ans

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int ans = -1001;

    public int maxPathSum(TreeNode root) {
        dfs(root);
        return ans;
    }

    private int dfs(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int left = Math.max(0, dfs(root.left));
        int right = Math.max(0, dfs(root.right));
        ans = Math.max(ans, root.val + left + right);
        return root.val + Math.max(left, right);
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxPathSum(TreeNode* root) {
        int ans = -1001;
        function<int(TreeNode*)> dfs = [&](TreeNode* root) {
            if (!root) {
                return 0;
            }
            int left = max(0, dfs(root->left));
            int right = max(0, dfs(root->right));
            ans = max(ans, left + right + root->val);
            return root->val + max(left, right);
        };
        dfs(root);
        return ans;
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func maxPathSum(root *TreeNode) int {
	ans := -1001
	var dfs func(*TreeNode) int
	dfs = func(root *TreeNode) int {
		if root == nil {
			return 0
		}
		left := max(0, dfs(root.Left))
		right := max(0, dfs(root.Right))
		ans = max(ans, left+right+root.Val)
		return max(left, right) + root.Val
	}
	dfs(root)
	return ans
}

TypeScript

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function maxPathSum(root: TreeNode | null): number {
    let ans = -1001;
    const dfs = (root: TreeNode | null): number => {
        if (!root) {
            return 0;
        }
        const left = Math.max(0, dfs(root.left));
        const right = Math.max(0, dfs(root.right));
        ans = Math.max(ans, left + right + root.val);
        return Math.max(left, right) + root.val;
    };
    dfs(root);
    return ans;
}

Rust

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
    fn dfs(root: &Option<Rc<RefCell<TreeNode>>>, res: &mut i32) -> i32 {
        if root.is_none() {
            return 0;
        }
        let node = root.as_ref().unwrap().borrow();
        let left = (0).max(Self::dfs(&node.left, res));
        let right = (0).max(Self::dfs(&node.right, res));
        *res = (node.val + left + right).max(*res);
        node.val + left.max(right)
    }

    pub fn max_path_sum(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
        let mut res = -1000;
        Self::dfs(&root, &mut res);
        res
    }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxPathSum = function (root) {
    let ans = -1001;
    const dfs = root => {
        if (!root) {
            return 0;
        }
        const left = Math.max(0, dfs(root.left));
        const right = Math.max(0, dfs(root.right));
        ans = Math.max(ans, left + right + root.val);
        return Math.max(left, right) + root.val;
    };
    dfs(root);
    return ans;
};

C#

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    private int ans = -1001;

    public int MaxPathSum(TreeNode root) {
        dfs(root);
        return ans;
    }

    private int dfs(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int left = Math.Max(0, dfs(root.left));
        int right = Math.Max(0, dfs(root.right));
        ans = Math.Max(ans, left + right + root.val);
        return root.val + Math.Max(left, right);
    }
}