| comments | difficulty | edit_url | tags | ||||
|---|---|---|---|---|---|---|---|
true |
Medium |
|
Given the root of a binary search tree, and an integer k, return the kth smallest value (1-indexed) of all the values of the nodes in the tree.
Example 1:
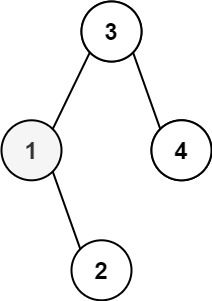
Input: root = [3,1,4,null,2], k = 1 Output: 1
Example 2:
Input: root = [5,3,6,2,4,null,null,1], k = 3 Output: 3
Constraints:
- The number of nodes in the tree is
n. 1 <= k <= n <= 1040 <= Node.val <= 104
Follow up: If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize?
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
stk = []
while root or stk:
if root:
stk.append(root)
root = root.left
else:
root = stk.pop()
k -= 1
if k == 0:
return root.val
root = root.right/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int kthSmallest(TreeNode root, int k) {
Deque<TreeNode> stk = new ArrayDeque<>();
while (root != null || !stk.isEmpty()) {
if (root != null) {
stk.push(root);
root = root.left;
} else {
root = stk.pop();
if (--k == 0) {
return root.val;
}
root = root.right;
}
}
return 0;
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int kthSmallest(TreeNode* root, int k) {
stack<TreeNode*> stk;
while (root || !stk.empty()) {
if (root) {
stk.push(root);
root = root->left;
} else {
root = stk.top();
stk.pop();
if (--k == 0) return root->val;
root = root->right;
}
}
return 0;
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func kthSmallest(root *TreeNode, k int) int {
stk := []*TreeNode{}
for root != nil || len(stk) > 0 {
if root != nil {
stk = append(stk, root)
root = root.Left
} else {
root = stk[len(stk)-1]
stk = stk[:len(stk)-1]
k--
if k == 0 {
return root.Val
}
root = root.Right
}
}
return 0
}/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function kthSmallest(root: TreeNode | null, k: number): number {
const dfs = (root: TreeNode | null) => {
if (root == null) {
return -1;
}
const { val, left, right } = root;
const l = dfs(left);
if (l !== -1) {
return l;
}
k--;
if (k === 0) {
return val;
}
return dfs(right);
};
return dfs(root);
}// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
// pub val: i32,
// pub left: Option<Rc<RefCell<TreeNode>>>,
// pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
// #[inline]
// pub fn new(val: i32) -> Self {
// TreeNode {
// val,
// left: None,
// right: None
// }
// }
// }
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
fn dfs(root: Option<Rc<RefCell<TreeNode>>>, res: &mut Vec<i32>, k: usize) {
if let Some(node) = root {
let mut node = node.borrow_mut();
Self::dfs(node.left.take(), res, k);
res.push(node.val);
if res.len() >= k {
return;
}
Self::dfs(node.right.take(), res, k);
}
}
pub fn kth_smallest(root: Option<Rc<RefCell<TreeNode>>>, k: i32) -> i32 {
let k = k as usize;
let mut res: Vec<i32> = Vec::with_capacity(k);
Self::dfs(root, &mut res, k);
res[k - 1]
}
}# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class BST:
def __init__(self, root):
self.cnt = Counter()
self.root = root
self.count(root)
def kthSmallest(self, k):
node = self.root
while node:
if self.cnt[node.left] == k - 1:
return node.val
if self.cnt[node.left] < k - 1:
k -= self.cnt[node.left] + 1
node = node.right
else:
node = node.left
return 0
def count(self, root):
if root is None:
return 0
n = 1 + self.count(root.left) + self.count(root.right)
self.cnt[root] = n
return n
class Solution:
def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
bst = BST(root)
return bst.kthSmallest(k)/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int kthSmallest(TreeNode root, int k) {
BST bst = new BST(root);
return bst.kthSmallest(k);
}
}
class BST {
private TreeNode root;
private Map<TreeNode, Integer> cnt = new HashMap<>();
public BST(TreeNode root) {
this.root = root;
count(root);
}
public int kthSmallest(int k) {
TreeNode node = root;
while (node != null) {
int v = node.left == null ? 0 : cnt.get(node.left);
if (v == k - 1) {
return node.val;
}
if (v < k - 1) {
node = node.right;
k -= (v + 1);
} else {
node = node.left;
}
}
return 0;
}
private int count(TreeNode root) {
if (root == null) {
return 0;
}
int n = 1 + count(root.left) + count(root.right);
cnt.put(root, n);
return n;
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class BST {
public:
BST(TreeNode* root)
: root(root) {
count(root);
}
int kthSmallest(int k) {
TreeNode* node = root;
while (node) {
int v = !node->left ? 0 : cnt[node->left];
if (v == k - 1) return node->val;
if (v < k - 1) {
node = node->right;
k -= (v + 1);
} else
node = node->left;
}
return 0;
}
private:
TreeNode* root;
unordered_map<TreeNode*, int> cnt;
int count(TreeNode* root) {
if (!root) return 0;
int n = 1 + count(root->left) + count(root->right);
cnt[root] = n;
return n;
}
};
class Solution {
public:
int kthSmallest(TreeNode* root, int k) {
BST bst(root);
return bst.kthSmallest(k);
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
type BST struct {
cnt map[*TreeNode]int
root *TreeNode
}
func newBST(root *TreeNode) *BST {
var count func(*TreeNode) int
cnt := map[*TreeNode]int{}
count = func(root *TreeNode) int {
if root == nil {
return 0
}
n := 1 + count(root.Left) + count(root.Right)
cnt[root] = n
return n
}
count(root)
return &BST{cnt, root}
}
func (bst *BST) kthSmallest(k int) int {
node := bst.root
for node != nil {
v := 0
if node.Left != nil {
v = bst.cnt[node.Left]
}
if v == k-1 {
return node.Val
}
if v < k-1 {
k -= (v + 1)
node = node.Right
} else {
node = node.Left
}
}
return 0
}
func kthSmallest(root *TreeNode, k int) int {
bst := newBST(root)
return bst.kthSmallest(k)
}