| comments | difficulty | edit_url | tags | |||
|---|---|---|---|---|---|---|
true |
Medium |
|
Given the root of a binary tree, return the number of uni-value subtrees.
A uni-value subtree means all nodes of the subtree have the same value.
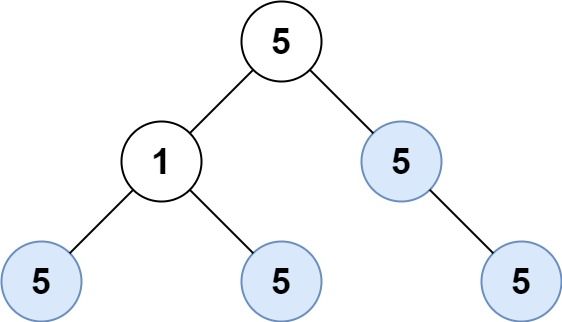
Example 1:
Input: root = [5,1,5,5,5,null,5] Output: 4
Example 2:
Input: root = [] Output: 0
Example 3:
Input: root = [5,5,5,5,5,null,5] Output: 6
Constraints:
- The number of the node in the tree will be in the range
[0, 1000]. -1000 <= Node.val <= 1000
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def countUnivalSubtrees(self, root: Optional[TreeNode]) -> int:
def dfs(root):
if root is None:
return True
l, r = dfs(root.left), dfs(root.right)
if not l or not r:
return False
a = root.val if root.left is None else root.left.val
b = root.val if root.right is None else root.right.val
if a == b == root.val:
nonlocal ans
ans += 1
return True
return False
ans = 0
dfs(root)
return ans/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private int ans;
public int countUnivalSubtrees(TreeNode root) {
dfs(root);
return ans;
}
private boolean dfs(TreeNode root) {
if (root == null) {
return true;
}
boolean l = dfs(root.left);
boolean r = dfs(root.right);
if (!l || !r) {
return false;
}
int a = root.left == null ? root.val : root.left.val;
int b = root.right == null ? root.val : root.right.val;
if (a == b && b == root.val) {
++ans;
return true;
}
return false;
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int countUnivalSubtrees(TreeNode* root) {
int ans = 0;
function<bool(TreeNode*)> dfs = [&](TreeNode* root) -> bool {
if (!root) {
return true;
}
bool l = dfs(root->left);
bool r = dfs(root->right);
if (!l || !r) {
return false;
}
int a = root->left ? root->left->val : root->val;
int b = root->right ? root->right->val : root->val;
if (a == b && b == root->val) {
++ans;
return true;
}
return false;
};
dfs(root);
return ans;
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func countUnivalSubtrees(root *TreeNode) (ans int) {
var dfs func(*TreeNode) bool
dfs = func(root *TreeNode) bool {
if root == nil {
return true
}
l, r := dfs(root.Left), dfs(root.Right)
if !l || !r {
return false
}
if root.Left != nil && root.Left.Val != root.Val {
return false
}
if root.Right != nil && root.Right.Val != root.Val {
return false
}
ans++
return true
}
dfs(root)
return
}/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function countUnivalSubtrees(root: TreeNode | null): number {
let ans: number = 0;
const dfs = (root: TreeNode | null): boolean => {
if (root == null) {
return true;
}
const l: boolean = dfs(root.left);
const r: boolean = dfs(root.right);
if (!l || !r) {
return false;
}
if (root.left != null && root.left.val != root.val) {
return false;
}
if (root.right != null && root.right.val != root.val) {
return false;
}
++ans;
return true;
};
dfs(root);
return ans;
}/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var countUnivalSubtrees = function (root) {
let ans = 0;
const dfs = root => {
if (!root) {
return true;
}
const l = dfs(root.left);
const r = dfs(root.right);
if (!l || !r) {
return false;
}
if (root.left && root.left.val !== root.val) {
return false;
}
if (root.right && root.right.val !== root.val) {
return false;
}
++ans;
return true;
};
dfs(root);
return ans;
};