README_EN.md

comments	difficulty	edit_url	tags
true	Medium	https://github.com/doocs/leetcode/edit/main/solution/0200-0299/0255.Verify%20Preorder%20Sequence%20in%20Binary%20Search%20Tree/README_EN.md	Stack Tree Binary Search Tree Recursion Array Binary Tree Monotonic Stack

255. Verify Preorder Sequence in Binary Search Tree 🔒

中文文档

Description

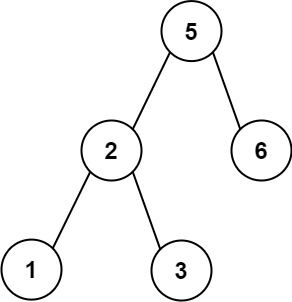
Given an array of unique integers preorder, return true if it is the correct preorder traversal sequence of a binary search tree.

 

Example 1:

Input: preorder = [5,2,1,3,6]
Output: true

Example 2:

Input: preorder = [5,2,6,1,3]
Output: false

 

Constraints:

• 1 <= preorder.length <= 104
• 1 <= preorder[i] <= 104
• All the elements of preorder are unique.

 

Follow up: Could you do it using only constant space complexity?

Solutions

Solution 1

Python3

class Solution:
    def verifyPreorder(self, preorder: List[int]) -> bool:
        stk = []
        last = -inf
        for x in preorder:
            if x < last:
                return False
            while stk and stk[-1] < x:
                last = stk.pop()
            stk.append(x)
        return True

Java

class Solution {
    public boolean verifyPreorder(int[] preorder) {
        Deque<Integer> stk = new ArrayDeque<>();
        int last = Integer.MIN_VALUE;
        for (int x : preorder) {
            if (x < last) {
                return false;
            }
            while (!stk.isEmpty() && stk.peek() < x) {
                last = stk.poll();
            }
            stk.push(x);
        }
        return true;
    }
}

C++

class Solution {
public:
    bool verifyPreorder(vector<int>& preorder) {
        stack<int> stk;
        int last = INT_MIN;
        for (int x : preorder) {
            if (x < last) return false;
            while (!stk.empty() && stk.top() < x) {
                last = stk.top();
                stk.pop();
            }
            stk.push(x);
        }
        return true;
    }
};

Go

func verifyPreorder(preorder []int) bool {
	var stk []int
	last := math.MinInt32
	for _, x := range preorder {
		if x < last {
			return false
		}
		for len(stk) > 0 && stk[len(stk)-1] < x {
			last = stk[len(stk)-1]
			stk = stk[0 : len(stk)-1]
		}
		stk = append(stk, x)
	}
	return true
}