Skip to content

Latest commit

 

History

History
366 lines (310 loc) · 8.53 KB

README_EN.md

File metadata and controls

366 lines (310 loc) · 8.53 KB
comments difficulty edit_url tags
true
Medium
Depth-First Search
Breadth-First Search
Union Find
Graph

261. Graph Valid Tree 🔒

中文文档

Description

You have a graph of n nodes labeled from 0 to n - 1. You are given an integer n and a list of edges where edges[i] = [ai, bi] indicates that there is an undirected edge between nodes ai and bi in the graph.

Return true if the edges of the given graph make up a valid tree, and false otherwise.

 

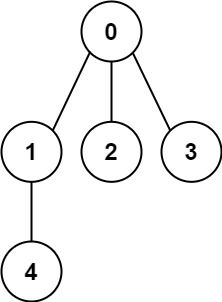
Example 1:

Input: n = 5, edges = [[0,1],[0,2],[0,3],[1,4]]
Output: true

Example 2:

Input: n = 5, edges = [[0,1],[1,2],[2,3],[1,3],[1,4]]
Output: false

 

Constraints:

  • 1 <= n <= 2000
  • 0 <= edges.length <= 5000
  • edges[i].length == 2
  • 0 <= ai, bi < n
  • ai != bi
  • There are no self-loops or repeated edges.

Solutions

Solution 1: Union-Find

To determine whether it is a tree, the following two conditions must be met:

  1. The number of edges is equal to the number of nodes minus one;
  2. There is no cycle.

We can use a union-find set to determine whether there is a cycle. We traverse the edges, if two nodes are already in the same set, it means there is a cycle. Otherwise, we merge the two nodes into the same set. Then we decrease the number of connected components by one, and finally check whether the number of connected components is $1$.

The time complexity is $O(n \times \log n)$, and the space complexity is $O(n)$, where $n$ is the number of nodes.

Python3

class Solution:
    def validTree(self, n: int, edges: List[List[int]]) -> bool:
        def find(x: int) -> int:
            if p[x] != x:
                p[x] = find(p[x])
            return p[x]

        p = list(range(n))
        for a, b in edges:
            pa, pb = find(a), find(b)
            if pa == pb:
                return False
            p[pa] = pb
            n -= 1
        return n == 1

Java

class Solution {
public:
    bool validTree(int n, vector<vector<int>>& edges) {
        vector<int> p(n);
        iota(p.begin(), p.end(), 0);
        function<int(int)> find = [&](int x) {
            if (p[x] != x) {
                p[x] = find(p[x]);
            }
            return p[x];
        };
        for (auto& e : edges) {
            int pa = find(e[0]), pb = find(e[1]);
            if (pa == pb) {
                return false;
            }
            p[pa] = pb;
            --n;
        }
        return n == 1;
    }
};

C++

class Solution {
public:
    vector<int> p;

    bool validTree(int n, vector<vector<int>>& edges) {
        p.resize(n);
        for (int i = 0; i < n; ++i) p[i] = i;
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            if (find(a) == find(b)) return 0;
            p[find(a)] = find(b);
            --n;
        }
        return n == 1;
    }

    int find(int x) {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }
};

Go

func validTree(n int, edges [][]int) bool {
	p := make([]int, n)
	for i := range p {
		p[i] = i
	}
	var find func(int) int
	find = func(x int) int {
		if p[x] != x {
			p[x] = find(p[x])
		}
		return p[x]
	}
	for _, e := range edges {
		pa, pb := find(e[0]), find(e[1])
		if pa == pb {
			return false
		}
		p[pa] = pb
		n--
	}
	return n == 1
}

JavaScript

/**
 * @param {number} n
 * @param {number[][]} edges
 * @return {boolean}
 */
var validTree = function (n, edges) {
    const p = Array.from({ length: n }, (_, i) => i);
    const find = x => {
        if (p[x] !== x) {
            p[x] = find(p[x]);
        }
        return p[x];
    };
    for (const [a, b] of edges) {
        const pa = find(a);
        const pb = find(b);
        if (pa === pb) {
            return false;
        }
        p[pa] = pb;
        --n;
    }
    return n === 1;
};

Solution 2: DFS

We can also use depth-first search to determine whether there is a cycle. We can use an array $vis$ to record the visited nodes. During the search, we first mark the node as visited, then traverse the nodes adjacent to this node. If the adjacent node has been visited, we skip it, otherwise we recursively visit the adjacent node. Finally, we check whether all nodes have been visited. If there are nodes that have not been visited, it means that it cannot form a tree, so we return false.

The time complexity is $O(n)$, and the space complexity is $O(n)$, where $n$ is the number of nodes.

Python3

class Solution:
    def validTree(self, n: int, edges: List[List[int]]) -> bool:
        def dfs(i: int):
            vis.add(i)
            for j in g[i]:
                if j not in vis:
                    dfs(j)

        if len(edges) != n - 1:
            return False
        g = [[] for _ in range(n)]
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        vis = set()
        dfs(0)
        return len(vis) == n

Java

class Solution {
    private List<Integer>[] g;
    private Set<Integer> vis = new HashSet<>();

    public boolean validTree(int n, int[][] edges) {
        if (edges.length != n - 1) {
            return false;
        }
        g = new List[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        for (var e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        dfs(0);
        return vis.size() == n;
    }

    private void dfs(int i) {
        vis.add(i);
        for (int j : g[i]) {
            if (!vis.contains(j)) {
                dfs(j);
            }
        }
    }
}

C++

class Solution {
public:
    bool validTree(int n, vector<vector<int>>& edges) {
        if (edges.size() != n - 1) {
            return false;
        }
        vector<int> g[n];
        vector<int> vis(n);
        function<void(int)> dfs = [&](int i) {
            vis[i] = true;
            --n;
            for (int j : g[i]) {
                if (!vis[j]) {
                    dfs(j);
                }
            }
        };
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].push_back(b);
            g[b].push_back(a);
        }
        dfs(0);
        return n == 0;
    }
};

Go

func validTree(n int, edges [][]int) bool {
	if len(edges) != n-1 {
		return false
	}
	g := make([][]int, n)
	vis := make([]bool, n)
	for _, e := range edges {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
	}
	var dfs func(int)
	dfs = func(i int) {
		vis[i] = true
		n--
		for _, j := range g[i] {
			if !vis[j] {
				dfs(j)
			}
		}
	}
	dfs(0)
	return n == 0
}

JavaScript

/**
 * @param {number} n
 * @param {number[][]} edges
 * @return {boolean}
 */
var validTree = function (n, edges) {
    if (edges.length !== n - 1) {
        return false;
    }
    const g = Array.from({ length: n }, () => []);
    const vis = Array.from({ length: n }, () => false);
    for (const [a, b] of edges) {
        g[a].push(b);
        g[b].push(a);
    }
    const dfs = i => {
        vis[i] = true;
        --n;
        for (const j of g[i]) {
            if (!vis[j]) {
                dfs(j);
            }
        }
    };
    dfs(0);
    return n === 0;
};