| comments | difficulty | edit_url | tags | ||||
|---|---|---|---|---|---|---|---|
true |
Medium |
|
Given the root of a binary tree, return the most frequent subtree sum. If there is a tie, return all the values with the highest frequency in any order.
The subtree sum of a node is defined as the sum of all the node values formed by the subtree rooted at that node (including the node itself).
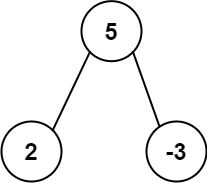
Example 1:
Input: root = [5,2,-3] Output: [2,-3,4]
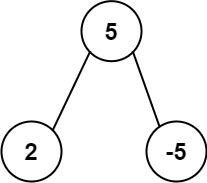
Example 2:
Input: root = [5,2,-5] Output: [2]
Constraints:
- The number of nodes in the tree is in the range
[1, 104]. -105 <= Node.val <= 105
We can use a hash table
Finally, we traverse
The time complexity is
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def findFrequentTreeSum(self, root: Optional[TreeNode]) -> List[int]:
def dfs(root: Optional[TreeNode]) -> int:
if root is None:
return 0
l, r = dfs(root.left), dfs(root.right)
s = l + r + root.val
cnt[s] += 1
return s
cnt = Counter()
dfs(root)
mx = max(cnt.values())
return [k for k, v in cnt.items() if v == mx]/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private Map<Integer, Integer> cnt = new HashMap<>();
private int mx;
public int[] findFrequentTreeSum(TreeNode root) {
dfs(root);
List<Integer> ans = new ArrayList<>();
for (var e : cnt.entrySet()) {
if (e.getValue() == mx) {
ans.add(e.getKey());
}
}
return ans.stream().mapToInt(i -> i).toArray();
}
private int dfs(TreeNode root) {
if (root == null) {
return 0;
}
int s = root.val + dfs(root.left) + dfs(root.right);
mx = Math.max(mx, cnt.merge(s, 1, Integer::sum));
return s;
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> findFrequentTreeSum(TreeNode* root) {
unordered_map<int, int> cnt;
int mx = 0;
function<int(TreeNode*)> dfs = [&](TreeNode* root) -> int {
if (!root) {
return 0;
}
int s = root->val + dfs(root->left) + dfs(root->right);
mx = max(mx, ++cnt[s]);
return s;
};
dfs(root);
vector<int> ans;
for (const auto& [k, v] : cnt) {
if (v == mx) {
ans.push_back(k);
}
}
return ans;
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func findFrequentTreeSum(root *TreeNode) (ans []int) {
cnt := map[int]int{}
var mx int
var dfs func(*TreeNode) int
dfs = func(root *TreeNode) int {
if root == nil {
return 0
}
s := root.Val + dfs(root.Left) + dfs(root.Right)
cnt[s]++
mx = max(mx, cnt[s])
return s
}
dfs(root)
for k, v := range cnt {
if v == mx {
ans = append(ans, k)
}
}
return
}/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function findFrequentTreeSum(root: TreeNode | null): number[] {
const cnt = new Map<number, number>();
let mx = 0;
const dfs = (root: TreeNode | null): number => {
if (!root) {
return 0;
}
const { val, left, right } = root;
const s = val + dfs(left) + dfs(right);
cnt.set(s, (cnt.get(s) ?? 0) + 1);
mx = Math.max(mx, cnt.get(s)!);
return s;
};
dfs(root);
return Array.from(cnt.entries())
.filter(([_, c]) => c === mx)
.map(([s, _]) => s);
}// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
// pub val: i32,
// pub left: Option<Rc<RefCell<TreeNode>>>,
// pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
// #[inline]
// pub fn new(val: i32) -> Self {
// TreeNode {
// val,
// left: None,
// right: None
// }
// }
// }
use std::cell::RefCell;
use std::collections::HashMap;
use std::rc::Rc;
impl Solution {
pub fn find_frequent_tree_sum(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
fn dfs(root: Option<Rc<RefCell<TreeNode>>>, cnt: &mut HashMap<i32, i32>) -> i32 {
if let Some(node) = root {
let l = dfs(node.borrow().left.clone(), cnt);
let r = dfs(node.borrow().right.clone(), cnt);
let s = l + r + node.borrow().val;
*cnt.entry(s).or_insert(0) += 1;
s
} else {
0
}
}
let mut cnt = HashMap::new();
dfs(root, &mut cnt);
let mx = cnt.values().cloned().max().unwrap_or(0);
cnt.into_iter()
.filter(|&(_, v)| v == mx)
.map(|(k, _)| k)
.collect()
}
}