| comments | difficulty | edit_url | tags | ||||
|---|---|---|---|---|---|---|---|
true |
Medium |
|
There is a directed graph of n nodes with each node labeled from 0 to n - 1. The graph is represented by a 0-indexed 2D integer array graph where graph[i] is an integer array of nodes adjacent to node i, meaning there is an edge from node i to each node in graph[i].
A node is a terminal node if there are no outgoing edges. A node is a safe node if every possible path starting from that node leads to a terminal node (or another safe node).
Return an array containing all the safe nodes of the graph. The answer should be sorted in ascending order.
Example 1:
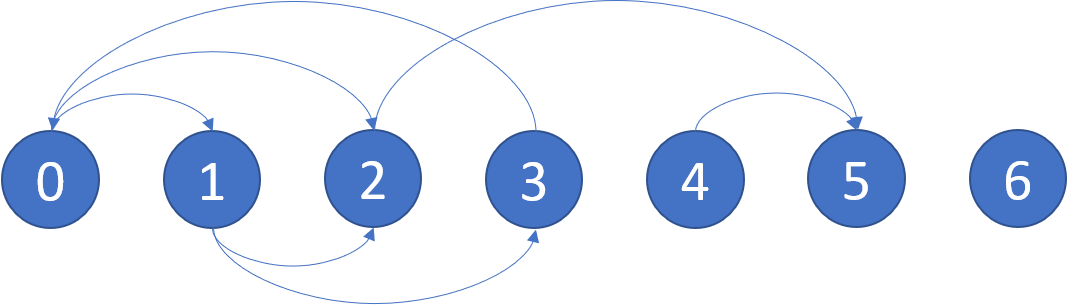
Input: graph = [[1,2],[2,3],[5],[0],[5],[],[]] Output: [2,4,5,6] Explanation: The given graph is shown above. Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them. Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.
Example 2:
Input: graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]] Output: [4] Explanation: Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.
Constraints:
n == graph.length1 <= n <= 1040 <= graph[i].length <= n0 <= graph[i][j] <= n - 1graph[i]is sorted in a strictly increasing order.- The graph may contain self-loops.
- The number of edges in the graph will be in the range
[1, 4 * 104].
class Solution:
def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]:
rg = defaultdict(list)
indeg = [0] * len(graph)
for i, vs in enumerate(graph):
for j in vs:
rg[j].append(i)
indeg[i] = len(vs)
q = deque([i for i, v in enumerate(indeg) if v == 0])
while q:
i = q.popleft()
for j in rg[i]:
indeg[j] -= 1
if indeg[j] == 0:
q.append(j)
return [i for i, v in enumerate(indeg) if v == 0]class Solution {
public List<Integer> eventualSafeNodes(int[][] graph) {
int n = graph.length;
int[] indeg = new int[n];
List<Integer>[] rg = new List[n];
Arrays.setAll(rg, k -> new ArrayList<>());
Deque<Integer> q = new ArrayDeque<>();
for (int i = 0; i < n; ++i) {
for (int j : graph[i]) {
rg[j].add(i);
}
indeg[i] = graph[i].length;
if (indeg[i] == 0) {
q.offer(i);
}
}
while (!q.isEmpty()) {
int i = q.pollFirst();
for (int j : rg[i]) {
if (--indeg[j] == 0) {
q.offer(j);
}
}
}
List<Integer> ans = new ArrayList<>();
for (int i = 0; i < n; ++i) {
if (indeg[i] == 0) {
ans.add(i);
}
}
return ans;
}
}class Solution {
public:
vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
int n = graph.size();
vector<int> indeg(n);
vector<vector<int>> rg(n);
queue<int> q;
for (int i = 0; i < n; ++i) {
for (int j : graph[i]) rg[j].push_back(i);
indeg[i] = graph[i].size();
if (indeg[i] == 0) q.push(i);
}
while (!q.empty()) {
int i = q.front();
q.pop();
for (int j : rg[i])
if (--indeg[j] == 0) q.push(j);
}
vector<int> ans;
for (int i = 0; i < n; ++i)
if (indeg[i] == 0) ans.push_back(i);
return ans;
}
};func eventualSafeNodes(graph [][]int) []int {
n := len(graph)
indeg := make([]int, n)
rg := make([][]int, n)
q := []int{}
for i, vs := range graph {
for _, j := range vs {
rg[j] = append(rg[j], i)
}
indeg[i] = len(vs)
if indeg[i] == 0 {
q = append(q, i)
}
}
for len(q) > 0 {
i := q[0]
q = q[1:]
for _, j := range rg[i] {
indeg[j]--
if indeg[j] == 0 {
q = append(q, j)
}
}
}
ans := []int{}
for i, v := range indeg {
if v == 0 {
ans = append(ans, i)
}
}
return ans
}/**
* @param {number[][]} graph
* @return {number[]}
*/
var eventualSafeNodes = function (graph) {
const n = graph.length;
const rg = new Array(n).fill(0).map(() => new Array());
const indeg = new Array(n).fill(0);
const q = [];
for (let i = 0; i < n; ++i) {
for (let j of graph[i]) {
rg[j].push(i);
}
indeg[i] = graph[i].length;
if (indeg[i] == 0) {
q.push(i);
}
}
while (q.length) {
const i = q.shift();
for (let j of rg[i]) {
if (--indeg[j] == 0) {
q.push(j);
}
}
}
let ans = [];
for (let i = 0; i < n; ++i) {
if (indeg[i] == 0) {
ans.push(i);
}
}
return ans;
};class Solution:
def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]:
def dfs(i):
if color[i]:
return color[i] == 2
color[i] = 1
for j in graph[i]:
if not dfs(j):
return False
color[i] = 2
return True
n = len(graph)
color = [0] * n
return [i for i in range(n) if dfs(i)]class Solution {
private int[] color;
private int[][] g;
public List<Integer> eventualSafeNodes(int[][] graph) {
int n = graph.length;
color = new int[n];
g = graph;
List<Integer> ans = new ArrayList<>();
for (int i = 0; i < n; ++i) {
if (dfs(i)) {
ans.add(i);
}
}
return ans;
}
private boolean dfs(int i) {
if (color[i] > 0) {
return color[i] == 2;
}
color[i] = 1;
for (int j : g[i]) {
if (!dfs(j)) {
return false;
}
}
color[i] = 2;
return true;
}
}class Solution {
public:
vector<int> color;
vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
int n = graph.size();
color.assign(n, 0);
vector<int> ans;
for (int i = 0; i < n; ++i)
if (dfs(i, graph)) ans.push_back(i);
return ans;
}
bool dfs(int i, vector<vector<int>>& g) {
if (color[i]) return color[i] == 2;
color[i] = 1;
for (int j : g[i])
if (!dfs(j, g)) return false;
color[i] = 2;
return true;
}
};func eventualSafeNodes(graph [][]int) []int {
n := len(graph)
color := make([]int, n)
var dfs func(int) bool
dfs = func(i int) bool {
if color[i] > 0 {
return color[i] == 2
}
color[i] = 1
for _, j := range graph[i] {
if !dfs(j) {
return false
}
}
color[i] = 2
return true
}
ans := []int{}
for i := range graph {
if dfs(i) {
ans = append(ans, i)
}
}
return ans
}/**
* @param {number[][]} graph
* @return {number[]}
*/
var eventualSafeNodes = function (graph) {
const n = graph.length;
const color = new Array(n).fill(0);
function dfs(i) {
if (color[i]) {
return color[i] == 2;
}
color[i] = 1;
for (const j of graph[i]) {
if (!dfs(j)) {
return false;
}
}
color[i] = 2;
return true;
}
let ans = [];
for (let i = 0; i < n; ++i) {
if (dfs(i)) {
ans.push(i);
}
}
return ans;
};