| comments | difficulty | edit_url | tags | ||||
|---|---|---|---|---|---|---|---|
true |
Hard |
|
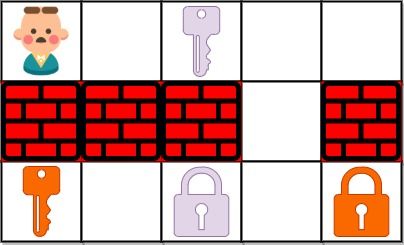
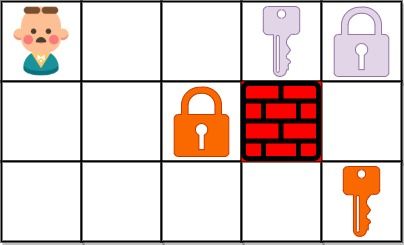
You are given an m x n grid grid where:
'.'is an empty cell.'#'is a wall.'@'is the starting point.- Lowercase letters represent keys.
- Uppercase letters represent locks.
You start at the starting point and one move consists of walking one space in one of the four cardinal directions. You cannot walk outside the grid, or walk into a wall.
If you walk over a key, you can pick it up and you cannot walk over a lock unless you have its corresponding key.
For some 1 <= k <= 6, there is exactly one lowercase and one uppercase letter of the first k letters of the English alphabet in the grid. This means that there is exactly one key for each lock, and one lock for each key; and also that the letters used to represent the keys and locks were chosen in the same order as the English alphabet.
Return the lowest number of moves to acquire all keys. If it is impossible, return -1.
Example 1:
Input: grid = ["@.a..","###.#","b.A.B"] Output: 8 Explanation: Note that the goal is to obtain all the keys not to open all the locks.
Example 2:
Input: grid = ["@..aA","..B#.","....b"] Output: 6
Example 3:
Input: grid = ["@Aa"] Output: -1
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 30grid[i][j]is either an English letter,'.','#', or'@'.- There is exactly one
'@'in the grid. - The number of keys in the grid is in the range
[1, 6]. - Each key in the grid is unique.
- Each key in the grid has a matching lock.
class Solution:
def shortestPathAllKeys(self, grid: List[str]) -> int:
m, n = len(grid), len(grid[0])
# 找起点 (si, sj)
si, sj = next((i, j) for i in range(m) for j in range(n) if grid[i][j] == '@')
# 统计钥匙数量
k = sum(v.islower() for row in grid for v in row)
dirs = (-1, 0, 1, 0, -1)
q = deque([(si, sj, 0)])
vis = {(si, sj, 0)}
ans = 0
while q:
for _ in range(len(q)):
i, j, state = q.popleft()
# 找到所有钥匙,返回当前步数
if state == (1 << k) - 1:
return ans
# 往四个方向搜索
for a, b in pairwise(dirs):
x, y = i + a, j + b
nxt = state
# 在边界范围内
if 0 <= x < m and 0 <= y < n:
c = grid[x][y]
# 是墙,或者是锁,但此时没有对应的钥匙,无法通过
if (
c == '#'
or c.isupper()
and (state & (1 << (ord(c) - ord('A')))) == 0
):
continue
# 是钥匙
if c.islower():
# 更新状态
nxt |= 1 << (ord(c) - ord('a'))
# 此状态未访问过,入队
if (x, y, nxt) not in vis:
vis.add((x, y, nxt))
q.append((x, y, nxt))
# 步数加一
ans += 1
return -1class Solution {
private int[] dirs = {-1, 0, 1, 0, -1};
public int shortestPathAllKeys(String[] grid) {
int m = grid.length, n = grid[0].length();
int k = 0;
int si = 0, sj = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
char c = grid[i].charAt(j);
if (Character.isLowerCase(c)) {
// 累加钥匙数量
++k;
} else if (c == '@') {
// 起点
si = i;
sj = j;
}
}
}
Deque<int[]> q = new ArrayDeque<>();
q.offer(new int[] {si, sj, 0});
boolean[][][] vis = new boolean[m][n][1 << k];
vis[si][sj][0] = true;
int ans = 0;
while (!q.isEmpty()) {
for (int t = q.size(); t > 0; --t) {
var p = q.poll();
int i = p[0], j = p[1], state = p[2];
// 找到所有钥匙,返回当前步数
if (state == (1 << k) - 1) {
return ans;
}
// 往四个方向搜索
for (int h = 0; h < 4; ++h) {
int x = i + dirs[h], y = j + dirs[h + 1];
// 在边界范围内
if (x >= 0 && x < m && y >= 0 && y < n) {
char c = grid[x].charAt(y);
// 是墙,或者是锁,但此时没有对应的钥匙,无法通过
if (c == '#'
|| (Character.isUpperCase(c) && ((state >> (c - 'A')) & 1) == 0)) {
continue;
}
int nxt = state;
// 是钥匙
if (Character.isLowerCase(c)) {
// 更新状态
nxt |= 1 << (c - 'a');
}
// 此状态未访问过,入队
if (!vis[x][y][nxt]) {
vis[x][y][nxt] = true;
q.offer(new int[] {x, y, nxt});
}
}
}
}
// 步数加一
++ans;
}
return -1;
}
}class Solution {
public:
const static inline vector<int> dirs = {-1, 0, 1, 0, -1};
int shortestPathAllKeys(vector<string>& grid) {
int m = grid.size(), n = grid[0].size();
int k = 0;
int si = 0, sj = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
char c = grid[i][j];
// 累加钥匙数量
if (islower(c)) ++k;
// 起点
else if (c == '@')
si = i, sj = j;
}
}
queue<tuple<int, int, int>> q{{{si, sj, 0}}};
vector<vector<vector<bool>>> vis(m, vector<vector<bool>>(n, vector<bool>(1 << k)));
vis[si][sj][0] = true;
int ans = 0;
while (!q.empty()) {
for (int t = q.size(); t; --t) {
auto [i, j, state] = q.front();
q.pop();
// 找到所有钥匙,返回当前步数
if (state == (1 << k) - 1) return ans;
// 往四个方向搜索
for (int h = 0; h < 4; ++h) {
int x = i + dirs[h], y = j + dirs[h + 1];
// 在边界范围内
if (x >= 0 && x < m && y >= 0 && y < n) {
char c = grid[x][y];
// 是墙,或者是锁,但此时没有对应的钥匙,无法通过
if (c == '#' || (isupper(c) && (state >> (c - 'A') & 1) == 0)) continue;
int nxt = state;
// 是钥匙,更新状态
if (islower(c)) nxt |= 1 << (c - 'a');
// 此状态未访问过,入队
if (!vis[x][y][nxt]) {
vis[x][y][nxt] = true;
q.push({x, y, nxt});
}
}
}
}
// 步数加一
++ans;
}
return -1;
}
};func shortestPathAllKeys(grid []string) int {
m, n := len(grid), len(grid[0])
var k, si, sj int
for i, row := range grid {
for j, c := range row {
if c >= 'a' && c <= 'z' {
// 累加钥匙数量
k++
} else if c == '@' {
// 起点
si, sj = i, j
}
}
}
type tuple struct{ i, j, state int }
q := []tuple{tuple{si, sj, 0}}
vis := map[tuple]bool{tuple{si, sj, 0}: true}
dirs := []int{-1, 0, 1, 0, -1}
ans := 0
for len(q) > 0 {
for t := len(q); t > 0; t-- {
p := q[0]
q = q[1:]
i, j, state := p.i, p.j, p.state
// 找到所有钥匙,返回当前步数
if state == 1<<k-1 {
return ans
}
// 往四个方向搜索
for h := 0; h < 4; h++ {
x, y := i+dirs[h], j+dirs[h+1]
// 在边界范围内
if x >= 0 && x < m && y >= 0 && y < n {
c := grid[x][y]
// 是墙,或者是锁,但此时没有对应的钥匙,无法通过
if c == '#' || (c >= 'A' && c <= 'Z' && (state>>(c-'A')&1 == 0)) {
continue
}
nxt := state
// 是钥匙,更新状态
if c >= 'a' && c <= 'z' {
nxt |= 1 << (c - 'a')
}
// 此状态未访问过,入队
if !vis[tuple{x, y, nxt}] {
vis[tuple{x, y, nxt}] = true
q = append(q, tuple{x, y, nxt})
}
}
}
}
// 步数加一
ans++
}
return -1
}