| comments | difficulty | edit_url | tags | |||
|---|---|---|---|---|---|---|
true |
Medium |
|
You are given an n x n integer matrix board where the cells are labeled from 1 to n2 in a Boustrophedon style starting from the bottom left of the board (i.e. board[n - 1][0]) and alternating direction each row.
You start on square 1 of the board. In each move, starting from square curr, do the following:
- Choose a destination square
nextwith a label in the range[curr + 1, min(curr + 6, n2)].<ul> <li>This choice simulates the result of a standard <strong>6-sided die roll</strong>: i.e., there are always at most 6 destinations, regardless of the size of the board.</li> </ul> </li> <li>If <code>next</code> has a snake or ladder, you <strong>must</strong> move to the destination of that snake or ladder. Otherwise, you move to <code>next</code>.</li> <li>The game ends when you reach the square <code>n<sup>2</sup></code>.</li>
A board square on row r and column c has a snake or ladder if board[r][c] != -1. The destination of that snake or ladder is board[r][c]. Squares 1 and n2 are not the starting points of any snake or ladder.
Note that you only take a snake or ladder at most once per move. If the destination to a snake or ladder is the start of another snake or ladder, you do not follow the subsequent snake or ladder.
- For example, suppose the board is
[[-1,4],[-1,3]], and on the first move, your destination square is2. You follow the ladder to square3, but do not follow the subsequent ladder to4.
Return the least number of moves required to reach the square n2. If it is not possible to reach the square, return -1.
Example 1:
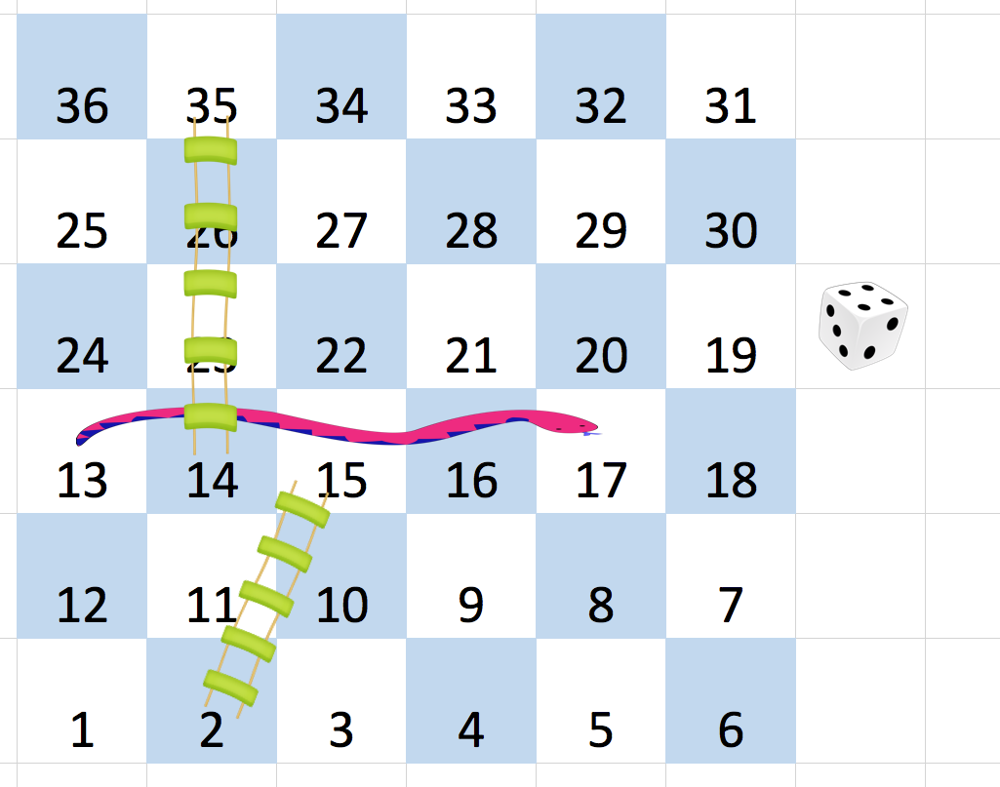
Input: board = [[-1,-1,-1,-1,-1,-1],[-1,-1,-1,-1,-1,-1],[-1,-1,-1,-1,-1,-1],[-1,35,-1,-1,13,-1],[-1,-1,-1,-1,-1,-1],[-1,15,-1,-1,-1,-1]] Output: 4 Explanation: In the beginning, you start at square 1 (at row 5, column 0). You decide to move to square 2 and must take the ladder to square 15. You then decide to move to square 17 and must take the snake to square 13. You then decide to move to square 14 and must take the ladder to square 35. You then decide to move to square 36, ending the game. This is the lowest possible number of moves to reach the last square, so return 4.
Example 2:
Input: board = [[-1,-1],[-1,3]] Output: 1
Constraints:
n == board.length == board[i].length2 <= n <= 20board[i][j]is either-1or in the range[1, n2].- The squares labeled
1andn2are not the starting points of any snake or ladder.
We can use the Breadth-First Search (BFS) method, starting from the starting point, moving forward 1 to 6 steps each time, and then checking for snakes or ladders. If there are any, move to the destination of the snake or ladder; otherwise, move to the next square.
Specifically, we use a queue
In each operation, we take out the square number
If the square corresponding to
If we ultimately cannot reach the endpoint, we return
The time complexity is
class Solution:
def snakesAndLadders(self, board: List[List[int]]) -> int:
n = len(board)
q = deque([1])
vis = {1}
ans = 0
m = n * n
while q:
for _ in range(len(q)):
x = q.popleft()
if x == m:
return ans
for y in range(x + 1, min(x + 6, m) + 1):
i, j = divmod(y - 1, n)
if i & 1:
j = n - j - 1
i = n - i - 1
z = y if board[i][j] == -1 else board[i][j]
if z not in vis:
vis.add(z)
q.append(z)
ans += 1
return -1class Solution {
public int snakesAndLadders(int[][] board) {
int n = board.length;
Deque<Integer> q = new ArrayDeque<>();
q.offer(1);
int m = n * n;
boolean[] vis = new boolean[m + 1];
vis[1] = true;
for (int ans = 0; !q.isEmpty(); ++ans) {
for (int k = q.size(); k > 0; --k) {
int x = q.poll();
if (x == m) {
return ans;
}
for (int y = x + 1; y <= Math.min(x + 6, m); ++y) {
int i = (y - 1) / n, j = (y - 1) % n;
if (i % 2 == 1) {
j = n - j - 1;
}
i = n - i - 1;
int z = board[i][j] == -1 ? y : board[i][j];
if (!vis[z]) {
vis[z] = true;
q.offer(z);
}
}
}
}
return -1;
}
}class Solution {
public:
int snakesAndLadders(vector<vector<int>>& board) {
int n = board.size();
queue<int> q{{1}};
int m = n * n;
vector<bool> vis(m + 1);
vis[1] = true;
for (int ans = 0; !q.empty(); ++ans) {
for (int k = q.size(); k > 0; --k) {
int x = q.front();
q.pop();
if (x == m) {
return ans;
}
for (int y = x + 1; y <= min(x + 6, m); ++y) {
int i = (y - 1) / n, j = (y - 1) % n;
if (i % 2 == 1) {
j = n - j - 1;
}
i = n - i - 1;
int z = board[i][j] == -1 ? y : board[i][j];
if (!vis[z]) {
vis[z] = true;
q.push(z);
}
}
}
}
return -1;
}
};func snakesAndLadders(board [][]int) int {
n := len(board)
q := []int{1}
m := n * n
vis := make([]bool, m+1)
vis[1] = true
for ans := 0; len(q) > 0; ans++ {
for k := len(q); k > 0; k-- {
x := q[0]
q = q[1:]
if x == m {
return ans
}
for y := x + 1; y <= min(x+6, m); y++ {
i, j := (y-1)/n, (y-1)%n
if i%2 == 1 {
j = n - j - 1
}
i = n - i - 1
z := y
if board[i][j] != -1 {
z = board[i][j]
}
if !vis[z] {
vis[z] = true
q = append(q, z)
}
}
}
}
return -1
}function snakesAndLadders(board: number[][]): number {
const n = board.length;
const q: number[] = [1];
const m = n * n;
const vis: boolean[] = Array(m + 1).fill(false);
vis[1] = true;
for (let ans = 0; q.length > 0; ans++) {
const nq: number[] = [];
for (const x of q) {
if (x === m) {
return ans;
}
for (let y = x + 1; y <= Math.min(x + 6, m); y++) {
let i = Math.floor((y - 1) / n);
let j = (y - 1) % n;
if (i % 2 === 1) {
j = n - j - 1;
}
i = n - i - 1;
const z = board[i][j] === -1 ? y : board[i][j];
if (!vis[z]) {
vis[z] = true;
nq.push(z);
}
}
}
q.length = 0;
for (const x of nq) {
q.push(x);
}
}
return -1;
}