| comments | difficulty | edit_url | tags | |||
|---|---|---|---|---|---|---|
true |
Medium |
|
You are given the root of a binary tree with n nodes where each node in the tree has node.val coins. There are n coins in total throughout the whole tree.
In one move, we may choose two adjacent nodes and move one coin from one node to another. A move may be from parent to child, or from child to parent.
Return the minimum number of moves required to make every node have exactly one coin.
Example 1:
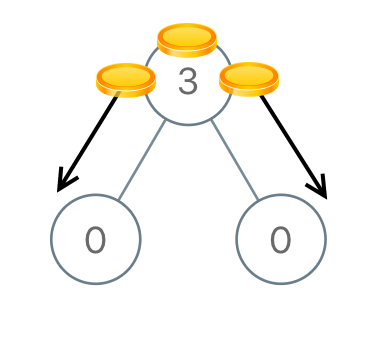
Input: root = [3,0,0] Output: 2 Explanation: From the root of the tree, we move one coin to its left child, and one coin to its right child.
Example 2:
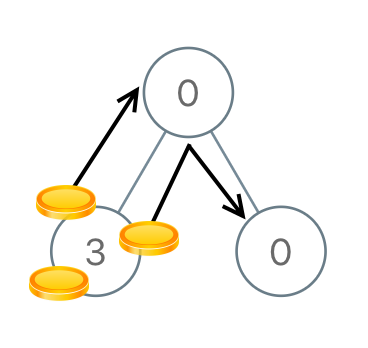
Input: root = [0,3,0] Output: 3 Explanation: From the left child of the root, we move two coins to the root [taking two moves]. Then, we move one coin from the root of the tree to the right child.
Constraints:
- The number of nodes in the tree is
n. 1 <= n <= 1000 <= Node.val <= n- The sum of all
Node.valisn.
We define a function
In the function
Finally, we return the number of moves.
The time complexity is
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def distributeCoins(self, root: Optional[TreeNode]) -> int:
def dfs(root):
if root is None:
return 0
left, right = dfs(root.left), dfs(root.right)
nonlocal ans
ans += abs(left) + abs(right)
return left + right + root.val - 1
ans = 0
dfs(root)
return ans/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private int ans;
public int distributeCoins(TreeNode root) {
dfs(root);
return ans;
}
private int dfs(TreeNode root) {
if (root == null) {
return 0;
}
int left = dfs(root.left);
int right = dfs(root.right);
ans += Math.abs(left) + Math.abs(right);
return left + right + root.val - 1;
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int distributeCoins(TreeNode* root) {
int ans = 0;
function<int(TreeNode*)> dfs = [&](TreeNode* root) -> int {
if (!root) {
return 0;
}
int left = dfs(root->left);
int right = dfs(root->right);
ans += abs(left) + abs(right);
return left + right + root->val - 1;
};
dfs(root);
return ans;
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func distributeCoins(root *TreeNode) (ans int) {
var dfs func(*TreeNode) int
dfs = func(root *TreeNode) int {
if root == nil {
return 0
}
left, right := dfs(root.Left), dfs(root.Right)
ans += abs(left) + abs(right)
return left + right + root.Val - 1
}
dfs(root)
return
}
func abs(x int) int {
if x < 0 {
return -x
}
return x
}/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function distributeCoins(root: TreeNode | null): number {
let ans = 0;
const dfs = (root: TreeNode | null) => {
if (!root) {
return 0;
}
const left = dfs(root.left);
const right = dfs(root.right);
ans += Math.abs(left) + Math.abs(right);
return left + right + root.val - 1;
};
dfs(root);
return ans;
}