| comments | difficulty | edit_url | rating | source | tags | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
true |
Medium |
1562 |
Weekly Contest 127 Q4 |
|
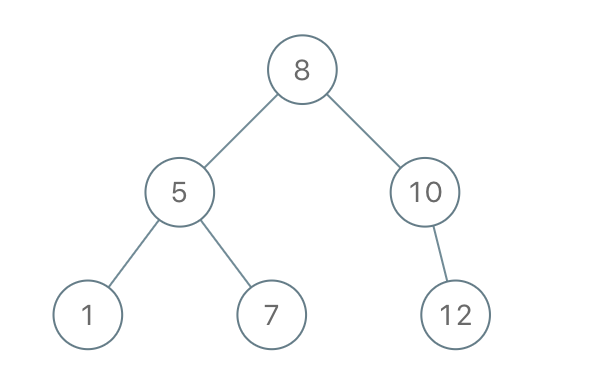
Given an array of integers preorder, which represents the preorder traversal of a BST (i.e., binary search tree), construct the tree and return its root.
It is guaranteed that there is always possible to find a binary search tree with the given requirements for the given test cases.
A binary search tree is a binary tree where for every node, any descendant of Node.left has a value strictly less than Node.val, and any descendant of Node.right has a value strictly greater than Node.val.
A preorder traversal of a binary tree displays the value of the node first, then traverses Node.left, then traverses Node.right.
Example 1:
Input: preorder = [8,5,1,7,10,12] Output: [8,5,10,1,7,null,12]
Example 2:
Input: preorder = [1,3] Output: [1,null,3]
Constraints:
1 <= preorder.length <= 1001 <= preorder[i] <= 1000- All the values of
preorderare unique.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def bstFromPreorder(self, preorder: List[int]) -> Optional[TreeNode]:
def dfs(preorder):
if not preorder:
return None
root = TreeNode(preorder[0])
left, right = 1, len(preorder)
while left < right:
mid = (left + right) >> 1
if preorder[mid] > preorder[0]:
right = mid
else:
left = mid + 1
root.left = dfs(preorder[1:left])
root.right = dfs(preorder[left:])
return root
return dfs(preorder)/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode bstFromPreorder(int[] preorder) {
return dfs(preorder, 0, preorder.length - 1);
}
private TreeNode dfs(int[] preorder, int i, int j) {
if (i > j || i >= preorder.length) {
return null;
}
TreeNode root = new TreeNode(preorder[i]);
int left = i + 1, right = j + 1;
while (left < right) {
int mid = (left + right) >> 1;
if (preorder[mid] > preorder[i]) {
right = mid;
} else {
left = mid + 1;
}
}
root.left = dfs(preorder, i + 1, left - 1);
root.right = dfs(preorder, left, j);
return root;
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* bstFromPreorder(vector<int>& preorder) {
return dfs(preorder, 0, preorder.size() - 1);
}
TreeNode* dfs(vector<int>& preorder, int i, int j) {
if (i > j || i >= preorder.size()) return nullptr;
TreeNode* root = new TreeNode(preorder[i]);
int left = i + 1, right = j + 1;
while (left < right) {
int mid = (left + right) >> 1;
if (preorder[mid] > preorder[i])
right = mid;
else
left = mid + 1;
}
root->left = dfs(preorder, i + 1, left - 1);
root->right = dfs(preorder, left, j);
return root;
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func bstFromPreorder(preorder []int) *TreeNode {
var dfs func(i, j int) *TreeNode
dfs = func(i, j int) *TreeNode {
if i > j || i >= len(preorder) {
return nil
}
root := &TreeNode{Val: preorder[i]}
left, right := i+1, len(preorder)
for left < right {
mid := (left + right) >> 1
if preorder[mid] > preorder[i] {
right = mid
} else {
left = mid + 1
}
}
root.Left = dfs(i+1, left-1)
root.Right = dfs(left, j)
return root
}
return dfs(0, len(preorder)-1)
}/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function bstFromPreorder(preorder: number[]): TreeNode | null {
const n = preorder.length;
const next = new Array(n);
const stack = [];
for (let i = n - 1; i >= 0; i--) {
while (stack.length !== 0 && preorder[stack[stack.length - 1]] < preorder[i]) {
stack.pop();
}
next[i] = stack[stack.length - 1] ?? n;
stack.push(i);
}
const dfs = (left: number, right: number) => {
if (left >= right) {
return null;
}
return new TreeNode(preorder[left], dfs(left + 1, next[left]), dfs(next[left], right));
};
return dfs(0, n);
}// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
// pub val: i32,
// pub left: Option<Rc<RefCell<TreeNode>>>,
// pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
// #[inline]
// pub fn new(val: i32) -> Self {
// TreeNode {
// val,
// left: None,
// right: None
// }
// }
// }
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
fn dfs(
preorder: &Vec<i32>,
next: &Vec<usize>,
left: usize,
right: usize,
) -> Option<Rc<RefCell<TreeNode>>> {
if left >= right {
return None;
}
Some(Rc::new(RefCell::new(TreeNode {
val: preorder[left],
left: Self::dfs(preorder, next, left + 1, next[left]),
right: Self::dfs(preorder, next, next[left], right),
})))
}
pub fn bst_from_preorder(preorder: Vec<i32>) -> Option<Rc<RefCell<TreeNode>>> {
let n = preorder.len();
let mut stack = Vec::new();
let mut next = vec![n; n];
for i in (0..n).rev() {
while !stack.is_empty() && preorder[*stack.last().unwrap()] < preorder[i] {
stack.pop();
}
if !stack.is_empty() {
next[i] = *stack.last().unwrap();
}
stack.push(i);
}
Self::dfs(&preorder, &next, 0, n)
}
}