| comments | difficulty | edit_url | rating | source | tags | ||
|---|---|---|---|---|---|---|---|
true |
Medium |
2130 |
Weekly Contest 135 Q3 |
|
You have a convex n-sided polygon where each vertex has an integer value. You are given an integer array values where values[i] is the value of the ith vertex in clockwise order.
Polygon triangulation is a process where you divide a polygon into a set of triangles and the vertices of each triangle must also be vertices of the original polygon. Note that no other shapes other than triangles are allowed in the division. This process will result in n - 2 triangles.
You will triangulate the polygon. For each triangle, the weight of that triangle is the product of the values at its vertices. The total score of the triangulation is the sum of these weights over all n - 2 triangles.
Return the minimum possible score that you can achieve with some triangulation of the polygon.
Example 1:
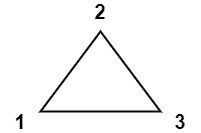
Input: values = [1,2,3]
Output: 6
Explanation: The polygon is already triangulated, and the score of the only triangle is 6.
Example 2:
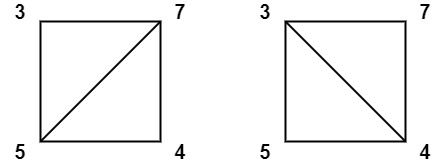
Input: values = [3,7,4,5]
Output: 144
Explanation: There are two triangulations, with possible scores: 3*7*5 + 4*5*7 = 245, or 3*4*5 + 3*4*7 = 144.
The minimum score is 144.
Example 3:
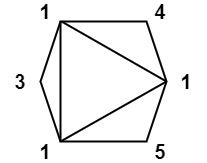
Input: values = [1,3,1,4,1,5]
Output: 13
Explanation: The minimum score triangulation is 1*1*3 + 1*1*4 + 1*1*5 + 1*1*1 = 13.
Constraints:
n == values.length3 <= n <= 501 <= values[i] <= 100
class Solution:
def minScoreTriangulation(self, values: List[int]) -> int:
@cache
def dfs(i: int, j: int) -> int:
if i + 1 == j:
return 0
return min(
dfs(i, k) + dfs(k, j) + values[i] * values[k] * values[j]
for k in range(i + 1, j)
)
return dfs(0, len(values) - 1)class Solution {
private int n;
private int[] values;
private Integer[][] f;
public int minScoreTriangulation(int[] values) {
n = values.length;
this.values = values;
f = new Integer[n][n];
return dfs(0, n - 1);
}
private int dfs(int i, int j) {
if (i + 1 == j) {
return 0;
}
if (f[i][j] != null) {
return f[i][j];
}
int ans = 1 << 30;
for (int k = i + 1; k < j; ++k) {
ans = Math.min(ans, dfs(i, k) + dfs(k, j) + values[i] * values[k] * values[j]);
}
return f[i][j] = ans;
}
}class Solution {
public:
int minScoreTriangulation(vector<int>& values) {
int n = values.size();
int f[n][n];
memset(f, 0, sizeof(f));
function<int(int, int)> dfs = [&](int i, int j) -> int {
if (i + 1 == j) {
return 0;
}
if (f[i][j]) {
return f[i][j];
}
int ans = 1 << 30;
for (int k = i + 1; k < j; ++k) {
ans = min(ans, dfs(i, k) + dfs(k, j) + values[i] * values[k] * values[j]);
}
return f[i][j] = ans;
};
return dfs(0, n - 1);
}
};func minScoreTriangulation(values []int) int {
n := len(values)
f := [50][50]int{}
var dfs func(int, int) int
dfs = func(i, j int) int {
if i+1 == j {
return 0
}
if f[i][j] != 0 {
return f[i][j]
}
f[i][j] = 1 << 30
for k := i + 1; k < j; k++ {
f[i][j] = min(f[i][j], dfs(i, k)+dfs(k, j)+values[i]*values[k]*values[j])
}
return f[i][j]
}
return dfs(0, n-1)
}function minScoreTriangulation(values: number[]): number {
const n = values.length;
const f: number[][] = Array.from({ length: n }, () => Array.from({ length: n }, () => 0));
const dfs = (i: number, j: number): number => {
if (i + 1 === j) {
return 0;
}
if (f[i][j] > 0) {
return f[i][j];
}
let ans = 1 << 30;
for (let k = i + 1; k < j; ++k) {
ans = Math.min(ans, dfs(i, k) + dfs(k, j) + values[i] * values[k] * values[j]);
}
f[i][j] = ans;
return ans;
};
return dfs(0, n - 1);
}class Solution:
def minScoreTriangulation(self, values: List[int]) -> int:
n = len(values)
f = [[0] * n for _ in range(n)]
for i in range(n - 3, -1, -1):
for j in range(i + 2, n):
f[i][j] = min(
f[i][k] + f[k][j] + values[i] * values[k] * values[j]
for k in range(i + 1, j)
)
return f[0][-1]class Solution {
public int minScoreTriangulation(int[] values) {
int n = values.length;
int[][] f = new int[n][n];
for (int i = n - 3; i >= 0; --i) {
for (int j = i + 2; j < n; ++j) {
f[i][j] = 1 << 30;
for (int k = i + 1; k < j; ++k) {
f[i][j]
= Math.min(f[i][j], f[i][k] + f[k][j] + values[i] * values[k] * values[j]);
}
}
}
return f[0][n - 1];
}
}class Solution {
public:
int minScoreTriangulation(vector<int>& values) {
int n = values.size();
int f[n][n];
memset(f, 0, sizeof(f));
for (int i = n - 3; i >= 0; --i) {
for (int j = i + 2; j < n; ++j) {
f[i][j] = 1 << 30;
for (int k = i + 1; k < j; ++k) {
f[i][j] = min(f[i][j], f[i][k] + f[k][j] + values[i] * values[k] * values[j]);
}
}
}
return f[0][n - 1];
}
};func minScoreTriangulation(values []int) int {
n := len(values)
f := [50][50]int{}
for i := n - 3; i >= 0; i-- {
for j := i + 2; j < n; j++ {
f[i][j] = 1 << 30
for k := i + 1; k < j; k++ {
f[i][j] = min(f[i][j], f[i][k]+f[k][j]+values[i]*values[k]*values[j])
}
}
}
return f[0][n-1]
}function minScoreTriangulation(values: number[]): number {
const n = values.length;
const f: number[][] = Array.from({ length: n }, () => Array.from({ length: n }, () => 0));
for (let i = n - 3; i >= 0; --i) {
for (let j = i + 2; j < n; ++j) {
f[i][j] = 1 << 30;
for (let k = i + 1; k < j; ++k) {
f[i][j] = Math.min(f[i][j], f[i][k] + f[k][j] + values[i] * values[k] * values[j]);
}
}
}
return f[0][n - 1];
}class Solution:
def minScoreTriangulation(self, values: List[int]) -> int:
n = len(values)
f = [[0] * n for _ in range(n)]
for l in range(3, n + 1):
for i in range(n - l + 1):
j = i + l - 1
f[i][j] = min(
f[i][k] + f[k][j] + values[i] * values[k] * values[j]
for k in range(i + 1, j)
)
return f[0][-1]class Solution {
public int minScoreTriangulation(int[] values) {
int n = values.length;
int[][] f = new int[n][n];
for (int l = 3; l <= n; ++l) {
for (int i = 0; i + l - 1 < n; ++i) {
int j = i + l - 1;
f[i][j] = 1 << 30;
for (int k = i + 1; k < j; ++k) {
f[i][j]
= Math.min(f[i][j], f[i][k] + f[k][j] + values[i] * values[k] * values[j]);
}
}
}
return f[0][n - 1];
}
}class Solution {
public:
int minScoreTriangulation(vector<int>& values) {
int n = values.size();
int f[n][n];
memset(f, 0, sizeof(f));
for (int l = 3; l <= n; ++l) {
for (int i = 0; i + l - 1 < n; ++i) {
int j = i + l - 1;
f[i][j] = 1 << 30;
for (int k = i + 1; k < j; ++k) {
f[i][j] = min(f[i][j], f[i][k] + f[k][j] + values[i] * values[k] * values[j]);
}
}
}
return f[0][n - 1];
}
};func minScoreTriangulation(values []int) int {
n := len(values)
f := [50][50]int{}
for l := 3; l <= n; l++ {
for i := 0; i+l-1 < n; i++ {
j := i + l - 1
f[i][j] = 1 << 30
for k := i + 1; k < j; k++ {
f[i][j] = min(f[i][j], f[i][k]+f[k][j]+values[i]*values[k]*values[j])
}
}
}
return f[0][n-1]
}function minScoreTriangulation(values: number[]): number {
const n = values.length;
const f: number[][] = Array.from({ length: n }, () => Array.from({ length: n }, () => 0));
for (let l = 3; l <= n; ++l) {
for (let i = 0; i + l - 1 < n; ++i) {
const j = i + l - 1;
f[i][j] = 1 << 30;
for (let k = i + 1; k < j; ++k) {
f[i][j] = Math.min(f[i][j], f[i][k] + f[k][j] + values[i] * values[k] * values[j]);
}
}
}
return f[0][n - 1];
}