Skip to content

Latest commit

 

History

History
432 lines (360 loc) · 12.5 KB

README_EN.md

File metadata and controls

432 lines (360 loc) · 12.5 KB
comments difficulty edit_url rating source tags
true
Medium
1919
Weekly Contest 146 Q3
Stack
Greedy
Array
Dynamic Programming
Monotonic Stack

1130. Minimum Cost Tree From Leaf Values

中文文档

Description

Given an array arr of positive integers, consider all binary trees such that:

  • Each node has either 0 or 2 children;
  • The values of arr correspond to the values of each leaf in an in-order traversal of the tree.
  • The value of each non-leaf node is equal to the product of the largest leaf value in its left and right subtree, respectively.

Among all possible binary trees considered, return the smallest possible sum of the values of each non-leaf node. It is guaranteed this sum fits into a 32-bit integer.

A node is a leaf if and only if it has zero children.

 

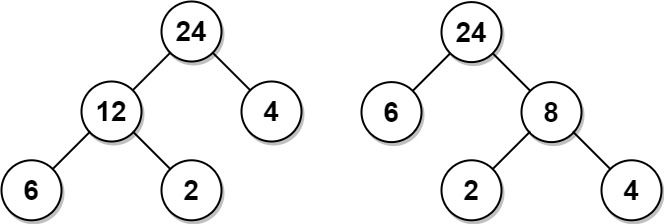
Example 1:

Input: arr = [6,2,4]
Output: 32
Explanation: There are two possible trees shown.
The first has a non-leaf node sum 36, and the second has non-leaf node sum 32.

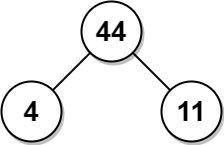
Example 2:

Input: arr = [4,11]
Output: 44

 

Constraints:

  • 2 <= arr.length <= 40
  • 1 <= arr[i] <= 15
  • It is guaranteed that the answer fits into a 32-bit signed integer (i.e., it is less than 231).

Solutions

Solution 1: Memoization Search

According to the problem description, the values in the array $arr$ correspond one-to-one with the values in the inorder traversal of each leaf node of the tree. We can divide the array into two non-empty sub-arrays, corresponding to the left and right subtrees of the tree, and recursively solve for the minimum possible sum of all non-leaf node values in each subtree.

We design a function $dfs(i, j)$, which represents the minimum possible sum of all non-leaf node values in the index range $[i, j]$ of the array $arr$. The answer is $dfs(0, n - 1)$, where $n$ is the length of the array $arr$.

The calculation process of the function $dfs(i, j)$ is as follows:

  • If $i = j$, it means that there is only one element in the array $arr[i..j]$, and there are no non-leaf nodes, so $dfs(i, j) = 0$.
  • Otherwise, we enumerate $k \in [i, j - 1]$, divide the array $arr$ into two sub-arrays $arr[i..k]$ and $arr[k + 1..j]$. For each $k$, we recursively calculate $dfs(i, k)$ and $dfs(k + 1, j)$. Here, $dfs(i, k)$ represents the minimum possible sum of all non-leaf node values in the index range $[i, k]$ of the array $arr$, and $dfs(k + 1, j)$ represents the minimum possible sum of all non-leaf node values in the index range $[k + 1, j]$ of the array $arr$. So $dfs(i, j) = \min_{i \leq k &lt; j} {dfs(i, k) + dfs(k + 1, j) + \max_{i \leq t \leq k} {arr[t]} \max_{k &lt; t \leq j} {arr[t]}}$.

In summary, we can get:

$$ dfs(i, j) = \begin{cases} 0, & \textit{if } i = j \\ \min_{i \leq k < j} {dfs(i, k) + dfs(k + 1, j) + \max_{i \leq t \leq k} {arr[t]} \max_{k < t \leq j} {arr[t]}}, & \textit{if } i < j \end{cases} $$

In the above recursive process, we can use the method of memoization search to avoid repeated calculations. Additionally, we can use an array $g$ to record the maximum value of all leaf nodes in the index range $[i, j]$ of the array $arr$. This allows us to optimize the calculation process of $dfs(i, j)$:

$$ dfs(i, j) = \begin{cases} 0, & \textit{if } i = j \\ \min_{i \leq k < j} {dfs(i, k) + dfs(k + 1, j) + g[i][k] \cdot g[k + 1][j]}, & \textit{if } i < j \end{cases} $$

Finally, we return $dfs(0, n - 1)$.

The time complexity is $O(n^3)$, and the space complexity is $O(n^2)$. Here, $n$ is the length of the array $arr$.

Python3

class Solution:
    def mctFromLeafValues(self, arr: List[int]) -> int:
        @cache
        def dfs(i: int, j: int) -> Tuple:
            if i == j:
                return 0, arr[i]
            s, mx = inf, -1
            for k in range(i, j):
                s1, mx1 = dfs(i, k)
                s2, mx2 = dfs(k + 1, j)
                t = s1 + s2 + mx1 * mx2
                if s > t:
                    s = t
                    mx = max(mx1, mx2)
            return s, mx

        return dfs(0, len(arr) - 1)[0]

Java

class Solution {
    private Integer[][] f;
    private int[][] g;

    public int mctFromLeafValues(int[] arr) {
        int n = arr.length;
        f = new Integer[n][n];
        g = new int[n][n];
        for (int i = n - 1; i >= 0; --i) {
            g[i][i] = arr[i];
            for (int j = i + 1; j < n; ++j) {
                g[i][j] = Math.max(g[i][j - 1], arr[j]);
            }
        }
        return dfs(0, n - 1);
    }

    private int dfs(int i, int j) {
        if (i == j) {
            return 0;
        }
        if (f[i][j] != null) {
            return f[i][j];
        }
        int ans = 1 << 30;
        for (int k = i; k < j; k++) {
            ans = Math.min(ans, dfs(i, k) + dfs(k + 1, j) + g[i][k] * g[k + 1][j]);
        }
        return f[i][j] = ans;
    }
}

C++

class Solution {
public:
    int mctFromLeafValues(vector<int>& arr) {
        int n = arr.size();
        int f[n][n];
        int g[n][n];
        memset(f, 0, sizeof(f));
        for (int i = n - 1; ~i; --i) {
            g[i][i] = arr[i];
            for (int j = i + 1; j < n; ++j) {
                g[i][j] = max(g[i][j - 1], arr[j]);
            }
        }
        function<int(int, int)> dfs = [&](int i, int j) -> int {
            if (i == j) {
                return 0;
            }
            if (f[i][j] > 0) {
                return f[i][j];
            }
            int ans = 1 << 30;
            for (int k = i; k < j; ++k) {
                ans = min(ans, dfs(i, k) + dfs(k + 1, j) + g[i][k] * g[k + 1][j]);
            }
            return f[i][j] = ans;
        };
        return dfs(0, n - 1);
    }
};

Go

func mctFromLeafValues(arr []int) int {
	n := len(arr)
	f := make([][]int, n)
	g := make([][]int, n)
	for i := range g {
		f[i] = make([]int, n)
		g[i] = make([]int, n)
		g[i][i] = arr[i]
		for j := i + 1; j < n; j++ {
			g[i][j] = max(g[i][j-1], arr[j])
		}
	}
	var dfs func(int, int) int
	dfs = func(i, j int) int {
		if i == j {
			return 0
		}
		if f[i][j] > 0 {
			return f[i][j]
		}
		f[i][j] = 1 << 30
		for k := i; k < j; k++ {
			f[i][j] = min(f[i][j], dfs(i, k)+dfs(k+1, j)+g[i][k]*g[k+1][j])
		}
		return f[i][j]
	}
	return dfs(0, n-1)
}

TypeScript

function mctFromLeafValues(arr: number[]): number {
    const n = arr.length;
    const f: number[][] = new Array(n).fill(0).map(() => new Array(n).fill(0));
    const g: number[][] = new Array(n).fill(0).map(() => new Array(n).fill(0));
    for (let i = n - 1; i >= 0; --i) {
        g[i][i] = arr[i];
        for (let j = i + 1; j < n; ++j) {
            g[i][j] = Math.max(g[i][j - 1], arr[j]);
        }
    }
    const dfs = (i: number, j: number): number => {
        if (i === j) {
            return 0;
        }
        if (f[i][j] > 0) {
            return f[i][j];
        }
        let ans = 1 << 30;
        for (let k = i; k < j; ++k) {
            ans = Math.min(ans, dfs(i, k) + dfs(k + 1, j) + g[i][k] * g[k + 1][j]);
        }
        return (f[i][j] = ans);
    };
    return dfs(0, n - 1);
}

Solution 2: Dynamic Programming

We can change the memoization search in Solution 1 to dynamic programming.

Define $f[i][j]$ to represent the minimum possible sum of all non-leaf node values in the index range $[i, j]$ of the array $arr$, and $g[i][j]$ to represent the maximum value of all leaf nodes in the index range $[i, j]$ of the array $arr$. Then, the state transition equation is:

$$ f[i][j] = \begin{cases} 0, & \textit{if } i = j \\ \min_{i \leq k < j} {f[i][k] + f[k + 1][j] + g[i][k] \cdot g[k + 1][j]}, & \textit{if } i < j \end{cases} $$

Finally, we return $f[0][n - 1]$.

The time complexity is $O(n^3)$, and the space complexity is $O(n^2)$. Here, $n$ is the length of the array $arr$.

Python3

class Solution:
    def mctFromLeafValues(self, arr: List[int]) -> int:
        @cache
        def dfs(i: int, j: int) -> int:
            if i == j:
                return 0
            return min(
                dfs(i, k) + dfs(k + 1, j) + g[i][k] * g[k + 1][j] for k in range(i, j)
            )

        n = len(arr)
        g = [[0] * n for _ in range(n)]
        for i in range(n - 1, -1, -1):
            g[i][i] = arr[i]
            for j in range(i + 1, n):
                g[i][j] = max(g[i][j - 1], arr[j])
        return dfs(0, n - 1)

Java

class Solution {
    public int mctFromLeafValues(int[] arr) {
        int n = arr.length;
        int[][] f = new int[n][n];
        int[][] g = new int[n][n];
        for (int i = n - 1; i >= 0; --i) {
            g[i][i] = arr[i];
            for (int j = i + 1; j < n; ++j) {
                g[i][j] = Math.max(g[i][j - 1], arr[j]);
                f[i][j] = 1 << 30;
                for (int k = i; k < j; ++k) {
                    f[i][j] = Math.min(f[i][j], f[i][k] + f[k + 1][j] + g[i][k] * g[k + 1][j]);
                }
            }
        }
        return f[0][n - 1];
    }
}

C++

class Solution {
public:
    int mctFromLeafValues(vector<int>& arr) {
        int n = arr.size();
        int f[n][n];
        int g[n][n];
        memset(f, 0, sizeof(f));
        for (int i = n - 1; ~i; --i) {
            g[i][i] = arr[i];
            for (int j = i + 1; j < n; ++j) {
                g[i][j] = max(g[i][j - 1], arr[j]);
                f[i][j] = 1 << 30;
                for (int k = i; k < j; ++k) {
                    f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j] + g[i][k] * g[k + 1][j]);
                }
            }
        }
        return f[0][n - 1];
    }
};

Go

func mctFromLeafValues(arr []int) int {
	n := len(arr)
	f := make([][]int, n)
	g := make([][]int, n)
	for i := range g {
		f[i] = make([]int, n)
		g[i] = make([]int, n)
	}
	for i := n - 1; i >= 0; i-- {
		g[i][i] = arr[i]
		for j := i + 1; j < n; j++ {
			g[i][j] = max(g[i][j-1], arr[j])
			f[i][j] = 1 << 30
			for k := i; k < j; k++ {
				f[i][j] = min(f[i][j], f[i][k]+f[k+1][j]+g[i][k]*g[k+1][j])
			}
		}
	}
	return f[0][n-1]
}

TypeScript

function mctFromLeafValues(arr: number[]): number {
    const n = arr.length;
    const f: number[][] = new Array(n).fill(0).map(() => new Array(n).fill(0));
    const g: number[][] = new Array(n).fill(0).map(() => new Array(n).fill(0));
    for (let i = n - 1; i >= 0; --i) {
        g[i][i] = arr[i];
        for (let j = i + 1; j < n; ++j) {
            g[i][j] = Math.max(g[i][j - 1], arr[j]);
            f[i][j] = 1 << 30;
            for (let k = i; k < j; ++k) {
                f[i][j] = Math.min(f[i][j], f[i][k] + f[k + 1][j] + g[i][k] * g[k + 1][j]);
            }
        }
    }
    return f[0][n - 1];
}

Solution 3

Python3

class Solution:
    def mctFromLeafValues(self, arr: List[int]) -> int:
        n = len(arr)
        f = [[0] * n for _ in range(n)]
        g = [[0] * n for _ in range(n)]
        for i in range(n - 1, -1, -1):
            g[i][i] = arr[i]
            for j in range(i + 1, n):
                g[i][j] = max(g[i][j - 1], arr[j])
                f[i][j] = min(
                    f[i][k] + f[k + 1][j] + g[i][k] * g[k + 1][j] for k in range(i, j)
                )
        return f[0][n - 1]