| comments | difficulty | edit_url | rating | source | tags | |||
|---|---|---|---|---|---|---|---|---|
true |
Hard |
1885 |
Weekly Contest 172 Q4 |
|
There is a one-dimensional garden on the x-axis. The garden starts at the point 0 and ends at the point n. (i.e., the length of the garden is n).
There are n + 1 taps located at points [0, 1, ..., n] in the garden.
Given an integer n and an integer array ranges of length n + 1 where ranges[i] (0-indexed) means the i-th tap can water the area [i - ranges[i], i + ranges[i]] if it was open.
Return the minimum number of taps that should be open to water the whole garden, If the garden cannot be watered return -1.
Example 1:
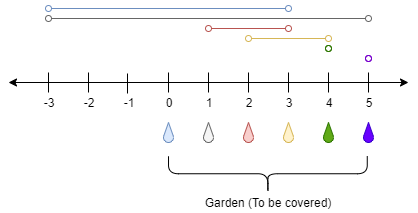
Input: n = 5, ranges = [3,4,1,1,0,0] Output: 1 Explanation: The tap at point 0 can cover the interval [-3,3] The tap at point 1 can cover the interval [-3,5] The tap at point 2 can cover the interval [1,3] The tap at point 3 can cover the interval [2,4] The tap at point 4 can cover the interval [4,4] The tap at point 5 can cover the interval [5,5] Opening Only the second tap will water the whole garden [0,5]
Example 2:
Input: n = 3, ranges = [0,0,0,0] Output: -1 Explanation: Even if you activate all the four taps you cannot water the whole garden.
Constraints:
1 <= n <= 104ranges.length == n + 10 <= ranges[i] <= 100
We note that for all taps that can cover a certain left endpoint, choosing the tap that can cover the farthest right endpoint is optimal.
Therefore, we can preprocess the array
Then we define the following three variables:
- Variable
$ans$ represents the final answer, i.e., the minimum number of taps; - Variable
$mx$ represents the farthest right endpoint that can currently be covered; - Variable
$pre$ represents the farthest right endpoint covered by the previous tap.
We traverse all positions in the range
- If
$mx \leq i$ , it means the next position cannot be covered, so we return$-1$ . - If
$pre = i$ , it means a new subinterval needs to be used, so we increment$ans$ by$1$ and update$pre = mx$ .
After the traversal, we return
The time complexity is
Similar problems:
class Solution:
def minTaps(self, n: int, ranges: List[int]) -> int:
last = [0] * (n + 1)
for i, x in enumerate(ranges):
l, r = max(0, i - x), i + x
last[l] = max(last[l], r)
ans = mx = pre = 0
for i in range(n):
mx = max(mx, last[i])
if mx <= i:
return -1
if pre == i:
ans += 1
pre = mx
return ansclass Solution {
public int minTaps(int n, int[] ranges) {
int[] last = new int[n + 1];
for (int i = 0; i < n + 1; ++i) {
int l = Math.max(0, i - ranges[i]), r = i + ranges[i];
last[l] = Math.max(last[l], r);
}
int ans = 0, mx = 0, pre = 0;
for (int i = 0; i < n; ++i) {
mx = Math.max(mx, last[i]);
if (mx <= i) {
return -1;
}
if (pre == i) {
++ans;
pre = mx;
}
}
return ans;
}
}class Solution {
public:
int minTaps(int n, vector<int>& ranges) {
vector<int> last(n + 1);
for (int i = 0; i < n + 1; ++i) {
int l = max(0, i - ranges[i]), r = i + ranges[i];
last[l] = max(last[l], r);
}
int ans = 0, mx = 0, pre = 0;
for (int i = 0; i < n; ++i) {
mx = max(mx, last[i]);
if (mx <= i) {
return -1;
}
if (pre == i) {
++ans;
pre = mx;
}
}
return ans;
}
};func minTaps(n int, ranges []int) (ans int) {
last := make([]int, n+1)
for i, x := range ranges {
l, r := max(0, i-x), i+x
last[l] = max(last[l], r)
}
var pre, mx int
for i, j := range last[:n] {
mx = max(mx, j)
if mx <= i {
return -1
}
if pre == i {
ans++
pre = mx
}
}
return
}function minTaps(n: number, ranges: number[]): number {
const last = new Array(n + 1).fill(0);
for (let i = 0; i < n + 1; ++i) {
const l = Math.max(0, i - ranges[i]);
const r = i + ranges[i];
last[l] = Math.max(last[l], r);
}
let ans = 0;
let mx = 0;
let pre = 0;
for (let i = 0; i < n; ++i) {
mx = Math.max(mx, last[i]);
if (mx <= i) {
return -1;
}
if (pre == i) {
++ans;
pre = mx;
}
}
return ans;
}impl Solution {
#[allow(dead_code)]
pub fn min_taps(n: i32, ranges: Vec<i32>) -> i32 {
let mut last = vec![0; (n + 1) as usize];
let mut ans = 0;
let mut mx = 0;
let mut pre = 0;
// Initialize the last vector
for (i, &r) in ranges.iter().enumerate() {
if (i as i32) - r >= 0 {
last[((i as i32) - r) as usize] =
std::cmp::max(last[((i as i32) - r) as usize], (i as i32) + r);
} else {
last[0] = std::cmp::max(last[0], (i as i32) + r);
}
}
for i in 0..n as usize {
mx = std::cmp::max(mx, last[i]);
if mx <= (i as i32) {
return -1;
}
if pre == (i as i32) {
ans += 1;
pre = mx;
}
}
ans
}
}