| comments | difficulty | edit_url | rating | source | tags | |
|---|---|---|---|---|---|---|
true |
Hard |
1844 |
Weekly Contest 184 Q4 |
|
You have a grid of size n x 3 and you want to paint each cell of the grid with exactly one of the three colors: Red, Yellow, or Green while making sure that no two adjacent cells have the same color (i.e., no two cells that share vertical or horizontal sides have the same color).
Given n the number of rows of the grid, return the number of ways you can paint this grid. As the answer may grow large, the answer must be computed modulo 109 + 7.
Example 1:
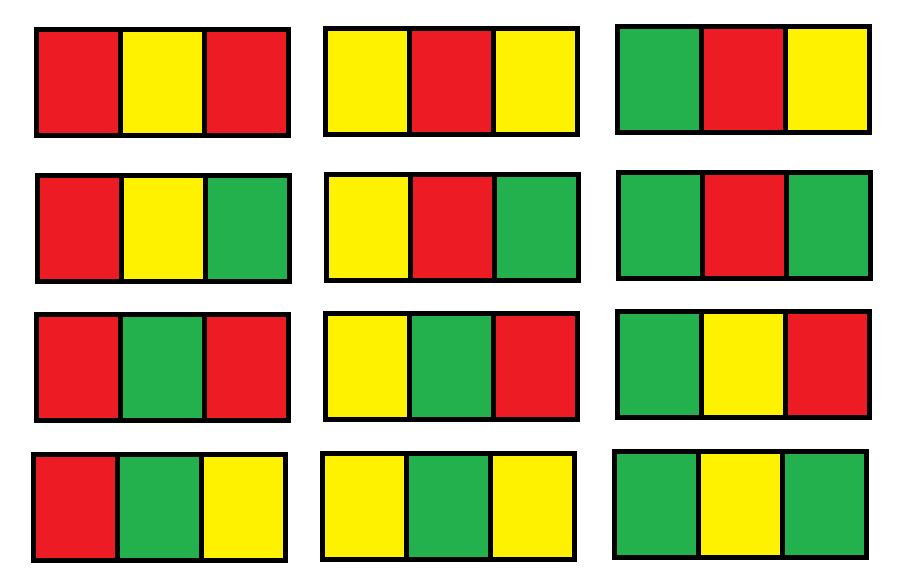
Input: n = 1 Output: 12 Explanation: There are 12 possible way to paint the grid as shown.
Example 2:
Input: n = 5000 Output: 30228214
Constraints:
n == grid.length1 <= n <= 5000
We classify all possible states for each row. According to the principle of symmetry, when a row only has
- When the state is
$010$ type: The possible states for the next row are:$101$ ,$102$ ,$121$ ,$201$ ,$202$ . These$5$ states can be summarized as$3$ $010$ types and$2$ $012$ types. - When the state is
$012$ type: The possible states for the next row are:$101$ ,$120$ ,$121$ ,$201$ . These$4$ states can be summarized as$2$ $010$ types and$2$ $012$ types.
In summary, we can get:
The time complexity is
class Solution:
def numOfWays(self, n: int) -> int:
mod = 10**9 + 7
f0 = f1 = 6
for _ in range(n - 1):
g0 = (3 * f0 + 2 * f1) % mod
g1 = (2 * f0 + 2 * f1) % mod
f0, f1 = g0, g1
return (f0 + f1) % modclass Solution {
public int numOfWays(int n) {
int mod = (int) 1e9 + 7;
long f0 = 6, f1 = 6;
for (int i = 0; i < n - 1; ++i) {
long g0 = (3 * f0 + 2 * f1) % mod;
long g1 = (2 * f0 + 2 * f1) % mod;
f0 = g0;
f1 = g1;
}
return (int) (f0 + f1) % mod;
}
}using ll = long long;
class Solution {
public:
int numOfWays(int n) {
int mod = 1e9 + 7;
ll f0 = 6, f1 = 6;
while (--n) {
ll g0 = (f0 * 3 + f1 * 2) % mod;
ll g1 = (f0 * 2 + f1 * 2) % mod;
f0 = g0;
f1 = g1;
}
return (int) (f0 + f1) % mod;
}
};func numOfWays(n int) int {
mod := int(1e9) + 7
f0, f1 := 6, 6
for n > 1 {
n--
g0 := (f0*3 + f1*2) % mod
g1 := (f0*2 + f1*2) % mod
f0, f1 = g0, g1
}
return (f0 + f1) % mod
}function numOfWays(n: number): number {
const mod: number = 10 ** 9 + 7;
let f0: number = 6;
let f1: number = 6;
for (let i = 1; i < n; i++) {
const g0: number = (3 * f0 + 2 * f1) % mod;
const g1: number = (2 * f0 + 2 * f1) % mod;
f0 = g0;
f1 = g1;
}
return (f0 + f1) % mod;
}We notice that the grid only has
Therefore, we define
where
The final answer is the sum of
We notice that
The time complexity is
class Solution:
def numOfWays(self, n: int) -> int:
def f1(x: int) -> bool:
last = -1
for _ in range(3):
if x % 3 == last:
return False
last = x % 3
x //= 3
return True
def f2(x: int, y: int) -> bool:
for _ in range(3):
if x % 3 == y % 3:
return False
x //= 3
y //= 3
return True
mod = 10**9 + 7
m = 27
valid = {i for i in range(m) if f1(i)}
d = defaultdict(list)
for i in valid:
for j in valid:
if f2(i, j):
d[i].append(j)
f = [int(i in valid) for i in range(m)]
for _ in range(n - 1):
g = [0] * m
for i in valid:
for j in d[i]:
g[j] = (g[j] + f[i]) % mod
f = g
return sum(f) % modclass Solution {
public int numOfWays(int n) {
final int mod = (int) 1e9 + 7;
int m = 27;
Set<Integer> valid = new HashSet<>();
int[] f = new int[m];
for (int i = 0; i < m; ++i) {
if (f1(i)) {
valid.add(i);
f[i] = 1;
}
}
Map<Integer, List<Integer>> d = new HashMap<>();
for (int i : valid) {
for (int j : valid) {
if (f2(i, j)) {
d.computeIfAbsent(i, k -> new ArrayList<>()).add(j);
}
}
}
for (int k = 1; k < n; ++k) {
int[] g = new int[m];
for (int i : valid) {
for (int j : d.getOrDefault(i, List.of())) {
g[j] = (g[j] + f[i]) % mod;
}
}
f = g;
}
int ans = 0;
for (int x : f) {
ans = (ans + x) % mod;
}
return ans;
}
private boolean f1(int x) {
int last = -1;
for (int i = 0; i < 3; ++i) {
if (x % 3 == last) {
return false;
}
last = x % 3;
x /= 3;
}
return true;
}
private boolean f2(int x, int y) {
for (int i = 0; i < 3; ++i) {
if (x % 3 == y % 3) {
return false;
}
x /= 3;
y /= 3;
}
return true;
}
}class Solution {
public:
int numOfWays(int n) {
int m = 27;
auto f1 = [&](int x) {
int last = -1;
for (int i = 0; i < 3; ++i) {
if (x % 3 == last) {
return false;
}
last = x % 3;
x /= 3;
}
return true;
};
auto f2 = [&](int x, int y) {
for (int i = 0; i < 3; ++i) {
if (x % 3 == y % 3) {
return false;
}
x /= 3;
y /= 3;
}
return true;
};
const int mod = 1e9 + 7;
unordered_set<int> valid;
vector<int> f(m);
for (int i = 0; i < m; ++i) {
if (f1(i)) {
valid.insert(i);
f[i] = 1;
}
}
unordered_map<int, vector<int>> d;
for (int i : valid) {
for (int j : valid) {
if (f2(i, j)) {
d[i].push_back(j);
}
}
}
for (int k = 1; k < n; ++k) {
vector<int> g(m);
for (int i : valid) {
for (int j : d[i]) {
g[j] = (g[j] + f[i]) % mod;
}
}
f = move(g);
}
int ans = 0;
for (int x : f) {
ans = (ans + x) % mod;
}
return ans;
}
};func numOfWays(n int) (ans int) {
f1 := func(x int) bool {
last := -1
for i := 0; i < 3; i++ {
if x%3 == last {
return false
}
last = x % 3
x /= 3
}
return true
}
f2 := func(x, y int) bool {
for i := 0; i < 3; i++ {
if x%3 == y%3 {
return false
}
x /= 3
y /= 3
}
return true
}
m := 27
valid := map[int]bool{}
f := make([]int, m)
for i := 0; i < m; i++ {
if f1(i) {
valid[i] = true
f[i] = 1
}
}
d := map[int][]int{}
for i := range valid {
for j := range valid {
if f2(i, j) {
d[i] = append(d[i], j)
}
}
}
const mod int = 1e9 + 7
for k := 1; k < n; k++ {
g := make([]int, m)
for i := range valid {
for _, j := range d[i] {
g[i] = (g[i] + f[j]) % mod
}
}
f = g
}
for _, x := range f {
ans = (ans + x) % mod
}
return
}function numOfWays(n: number): number {
const f1 = (x: number): boolean => {
let last = -1;
for (let i = 0; i < 3; ++i) {
if (x % 3 === last) {
return false;
}
last = x % 3;
x = Math.floor(x / 3);
}
return true;
};
const f2 = (x: number, y: number): boolean => {
for (let i = 0; i < 3; ++i) {
if (x % 3 === y % 3) {
return false;
}
x = Math.floor(x / 3);
y = Math.floor(y / 3);
}
return true;
};
const m = 27;
const valid = new Set<number>();
const f: number[] = Array(m).fill(0);
for (let i = 0; i < m; ++i) {
if (f1(i)) {
valid.add(i);
f[i] = 1;
}
}
const d: Map<number, number[]> = new Map();
for (const i of valid) {
for (const j of valid) {
if (f2(i, j)) {
d.set(i, (d.get(i) || []).concat(j));
}
}
}
const mod = 10 ** 9 + 7;
for (let k = 1; k < n; ++k) {
const g: number[] = Array(m).fill(0);
for (const i of valid) {
for (const j of d.get(i) || []) {
g[i] = (g[i] + f[j]) % mod;
}
}
f.splice(0, f.length, ...g);
}
let ans = 0;
for (const x of f) {
ans = (ans + x) % mod;
}
return ans;
}