| comments | difficulty | edit_url | rating | source | tags | ||||
|---|---|---|---|---|---|---|---|---|---|
true |
Medium |
1692 |
Biweekly Contest 27 Q3 |
|
There are a total of numCourses courses you have to take, labeled from 0 to numCourses - 1. You are given an array prerequisites where prerequisites[i] = [ai, bi] indicates that you must take course ai first if you want to take course bi.
- For example, the pair
[0, 1]indicates that you have to take course0before you can take course1.
Prerequisites can also be indirect. If course a is a prerequisite of course b, and course b is a prerequisite of course c, then course a is a prerequisite of course c.
You are also given an array queries where queries[j] = [uj, vj]. For the jth query, you should answer whether course uj is a prerequisite of course vj or not.
Return a boolean array answer, where answer[j] is the answer to the jth query.
Example 1:
Input: numCourses = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]] Output: [false,true] Explanation: The pair [1, 0] indicates that you have to take course 1 before you can take course 0. Course 0 is not a prerequisite of course 1, but the opposite is true.
Example 2:
Input: numCourses = 2, prerequisites = [], queries = [[1,0],[0,1]] Output: [false,false] Explanation: There are no prerequisites, and each course is independent.
Example 3:
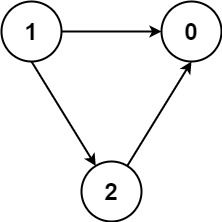
Input: numCourses = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]] Output: [true,true]
Constraints:
2 <= numCourses <= 1000 <= prerequisites.length <= (numCourses * (numCourses - 1) / 2)prerequisites[i].length == 20 <= ai, bi <= numCourses - 1ai != bi- All the pairs
[ai, bi]are unique. - The prerequisites graph has no cycles.
1 <= queries.length <= 1040 <= ui, vi <= numCourses - 1ui != vi
We create a 2D array
Next, we iterate through the prerequisites array
Then, we use Floyd's algorithm to compute the reachability between all pairs of nodes.
Specifically, we use three nested loops: first enumerating the intermediate node
After computing the reachability between all pairs of nodes, for each query
The time complexity is
class Solution:
def checkIfPrerequisite(
self, n: int, prerequisites: List[List[int]], queries: List[List[int]]
) -> List[bool]:
f = [[False] * n for _ in range(n)]
for a, b in prerequisites:
f[a][b] = True
for k in range(n):
for i in range(n):
for j in range(n):
if f[i][k] and f[k][j]:
f[i][j] = True
return [f[a][b] for a, b in queries]class Solution {
public List<Boolean> checkIfPrerequisite(int n, int[][] prerequisites, int[][] queries) {
boolean[][] f = new boolean[n][n];
for (var p : prerequisites) {
f[p[0]][p[1]] = true;
}
for (int k = 0; k < n; ++k) {
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
f[i][j] |= f[i][k] && f[k][j];
}
}
}
List<Boolean> ans = new ArrayList<>();
for (var q : queries) {
ans.add(f[q[0]][q[1]]);
}
return ans;
}
}class Solution {
public:
vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
bool f[n][n];
memset(f, false, sizeof(f));
for (auto& p : prerequisites) {
f[p[0]][p[1]] = true;
}
for (int k = 0; k < n; ++k) {
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
f[i][j] |= (f[i][k] && f[k][j]);
}
}
}
vector<bool> ans;
for (auto& q : queries) {
ans.push_back(f[q[0]][q[1]]);
}
return ans;
}
};func checkIfPrerequisite(n int, prerequisites [][]int, queries [][]int) (ans []bool) {
f := make([][]bool, n)
for i := range f {
f[i] = make([]bool, n)
}
for _, p := range prerequisites {
f[p[0]][p[1]] = true
}
for k := 0; k < n; k++ {
for i := 0; i < n; i++ {
for j := 0; j < n; j++ {
f[i][j] = f[i][j] || (f[i][k] && f[k][j])
}
}
}
for _, q := range queries {
ans = append(ans, f[q[0]][q[1]])
}
return
}function checkIfPrerequisite(n: number, prerequisites: number[][], queries: number[][]): boolean[] {
const f = Array.from({ length: n }, () => Array(n).fill(false));
prerequisites.forEach(([a, b]) => (f[a][b] = true));
for (let k = 0; k < n; ++k) {
for (let i = 0; i < n; ++i) {
for (let j = 0; j < n; ++j) {
f[i][j] ||= f[i][k] && f[k][j];
}
}
}
return queries.map(([a, b]) => f[a][b]);
}Similar to Solution 1, we create a 2D array
Next, we iterate through the prerequisites array
Then, we use topological sorting to compute the reachability between all pairs of nodes.
We define a queue
After computing the reachability between all pairs of nodes, for each query
The time complexity is
class Solution:
def checkIfPrerequisite(
self, n: int, prerequisites: List[List[int]], queries: List[List[int]]
) -> List[bool]:
f = [[False] * n for _ in range(n)]
g = [[] for _ in range(n)]
indeg = [0] * n
for a, b in prerequisites:
g[a].append(b)
indeg[b] += 1
q = deque(i for i, x in enumerate(indeg) if x == 0)
while q:
i = q.popleft()
for j in g[i]:
f[i][j] = True
for h in range(n):
f[h][j] = f[h][j] or f[h][i]
indeg[j] -= 1
if indeg[j] == 0:
q.append(j)
return [f[a][b] for a, b in queries]class Solution {
public List<Boolean> checkIfPrerequisite(int n, int[][] prerequisites, int[][] queries) {
boolean[][] f = new boolean[n][n];
List<Integer>[] g = new List[n];
int[] indeg = new int[n];
Arrays.setAll(g, i -> new ArrayList<>());
for (var p : prerequisites) {
g[p[0]].add(p[1]);
++indeg[p[1]];
}
Deque<Integer> q = new ArrayDeque<>();
for (int i = 0; i < n; ++i) {
if (indeg[i] == 0) {
q.offer(i);
}
}
while (!q.isEmpty()) {
int i = q.poll();
for (int j : g[i]) {
f[i][j] = true;
for (int h = 0; h < n; ++h) {
f[h][j] |= f[h][i];
}
if (--indeg[j] == 0) {
q.offer(j);
}
}
}
List<Boolean> ans = new ArrayList<>();
for (var qry : queries) {
ans.add(f[qry[0]][qry[1]]);
}
return ans;
}
}class Solution {
public:
vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
bool f[n][n];
memset(f, false, sizeof(f));
vector<int> g[n];
vector<int> indeg(n);
for (auto& p : prerequisites) {
g[p[0]].push_back(p[1]);
++indeg[p[1]];
}
queue<int> q;
for (int i = 0; i < n; ++i) {
if (indeg[i] == 0) {
q.push(i);
}
}
while (!q.empty()) {
int i = q.front();
q.pop();
for (int j : g[i]) {
f[i][j] = true;
for (int h = 0; h < n; ++h) {
f[h][j] |= f[h][i];
}
if (--indeg[j] == 0) {
q.push(j);
}
}
}
vector<bool> ans;
for (auto& qry : queries) {
ans.push_back(f[qry[0]][qry[1]]);
}
return ans;
}
};func checkIfPrerequisite(n int, prerequisites [][]int, queries [][]int) (ans []bool) {
f := make([][]bool, n)
for i := range f {
f[i] = make([]bool, n)
}
g := make([][]int, n)
indeg := make([]int, n)
for _, p := range prerequisites {
a, b := p[0], p[1]
g[a] = append(g[a], b)
indeg[b]++
}
q := []int{}
for i, x := range indeg {
if x == 0 {
q = append(q, i)
}
}
for len(q) > 0 {
i := q[0]
q = q[1:]
for _, j := range g[i] {
f[i][j] = true
for h := 0; h < n; h++ {
f[h][j] = f[h][j] || f[h][i]
}
indeg[j]--
if indeg[j] == 0 {
q = append(q, j)
}
}
}
for _, q := range queries {
ans = append(ans, f[q[0]][q[1]])
}
return
}function checkIfPrerequisite(n: number, prerequisites: number[][], queries: number[][]): boolean[] {
const f = Array.from({ length: n }, () => Array(n).fill(false));
const g: number[][] = Array.from({ length: n }, () => []);
const indeg: number[] = Array(n).fill(0);
for (const [a, b] of prerequisites) {
g[a].push(b);
++indeg[b];
}
const q: number[] = [];
for (let i = 0; i < n; ++i) {
if (indeg[i] === 0) {
q.push(i);
}
}
while (q.length) {
const i = q.shift()!;
for (const j of g[i]) {
f[i][j] = true;
for (let h = 0; h < n; ++h) {
f[h][j] ||= f[h][i];
}
if (--indeg[j] === 0) {
q.push(j);
}
}
}
return queries.map(([a, b]) => f[a][b]);
}