| comments | difficulty | edit_url | tags | |||||
|---|---|---|---|---|---|---|---|---|
true |
Medium |
|
You are given a 0-indexed integer array order of length n, a permutation of integers from 1 to n representing the order of insertion into a binary search tree.
A binary search tree is defined as follows:
- The left subtree of a node contains only nodes with keys less than the node's key.
- The right subtree of a node contains only nodes with keys greater than the node's key.
- Both the left and right subtrees must also be binary search trees.
The binary search tree is constructed as follows:
order[0]will be the root of the binary search tree.- All subsequent elements are inserted as the child of any existing node such that the binary search tree properties hold.
Return the depth of the binary search tree.
A binary tree's depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
Example 1:
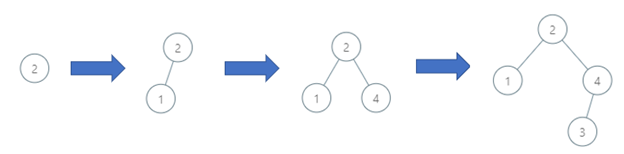
Input: order = [2,1,4,3] Output: 3 Explanation: The binary search tree has a depth of 3 with path 2->3->4.
Example 2:
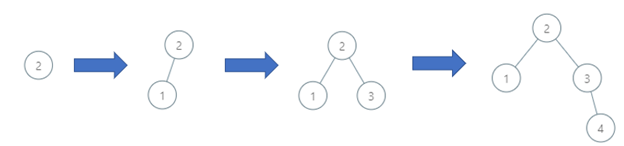
Input: order = [2,1,3,4] Output: 3 Explanation: The binary search tree has a depth of 3 with path 2->3->4.
Example 3:
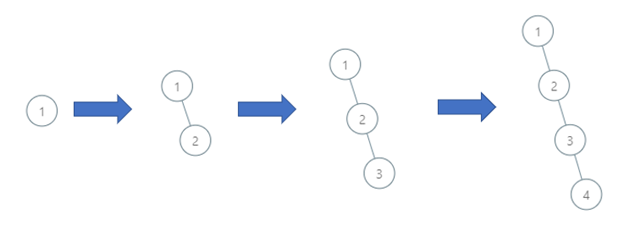
Input: order = [1,2,3,4] Output: 4 Explanation: The binary search tree has a depth of 4 with path 1->2->3->4.
Constraints:
n == order.length1 <= n <= 105orderis a permutation of integers between1andn.
from sortedcontainers import SortedDict
class Solution:
def maxDepthBST(self, order: List[int]) -> int:
sd = SortedDict({0: 0, inf: 0, order[0]: 1})
ans = 1
for v in order[1:]:
lower = sd.bisect_left(v) - 1
higher = lower + 1
depth = 1 + max(sd.values()[lower], sd.values()[higher])
ans = max(ans, depth)
sd[v] = depth
return ansclass Solution {
public int maxDepthBST(int[] order) {
TreeMap<Integer, Integer> tm = new TreeMap<>();
tm.put(0, 0);
tm.put(Integer.MAX_VALUE, 0);
tm.put(order[0], 1);
int ans = 1;
for (int i = 1; i < order.length; ++i) {
int v = order[i];
Map.Entry<Integer, Integer> lower = tm.lowerEntry(v);
Map.Entry<Integer, Integer> higher = tm.higherEntry(v);
int depth = 1 + Math.max(lower.getValue(), higher.getValue());
ans = Math.max(ans, depth);
tm.put(v, depth);
}
return ans;
}
}