| comments | difficulty | edit_url | tags | ||||
|---|---|---|---|---|---|---|---|
true |
中等 |
|
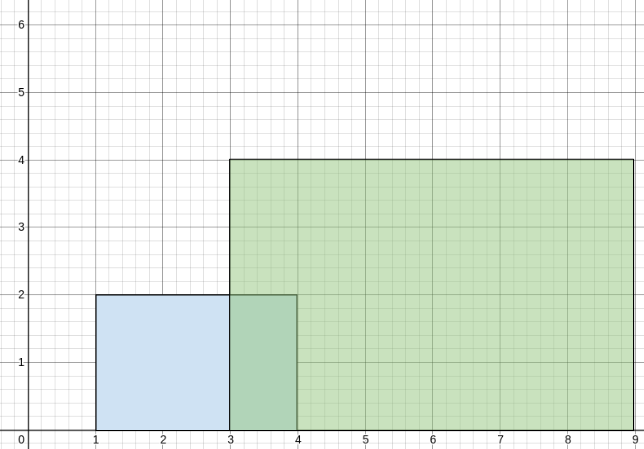
一条完全笔直的街道由一条数字线表示。街道上有建筑物,由二维整数阵列 buildings 表示,其中 buildings[i] = [starti, endi, heighti]。这意味着在 半封闭的位置[starti,endi) 有一座高度为 heighti 的建筑。
你想用 最少 数量的非重叠 部分 来 描述 街道上建筑物的高度。街道可以用2D整数数组 street 来表示,其中 street[j] = [leftj, rightj, averagej] 描述了道路的 半封闭区域 [leftj, rightj) ,该段中建筑物的 平均 高度为 averagej 。
- 例如,如果
buildings = [[1,5,2],[3,10,4]],street = [[1,3,2],[3,5,3],[5,10,4]]可以表示街道,因为:<ul> <li>从 1 到 3 ,只有第一栋建筑的平均高度为 <code>2 / 1 = 2</code> 。</li> <li>从 3 到 5 ,第一和第二栋建筑的平均高度均为 <code>(2+4) / 2 = 3 </code>。</li> <li>从 5 到 10 ,只有第二栋建筑的平均高度为 <code>4 / 1 = 4</code> 。</li> </ul> </li>
给定 buildings ,返回如上所述的二维整数矩阵 street ( 不包括 街道上没有建筑物的任何区域)。您可以按 任何顺序 返回数组。
n 个元素的 平均值 是 n 个元素除以 n 的 总和 (整数除法)。
半闭合段 [a, b) 是点 a 和 b 之间的数字线的截面,包括 点 a ,不包括 点 b 。
示例1:
输入: buildings = [[1,4,2],[3,9,4]] 输出: [[1,3,2],[3,4,3],[4,9,4]] 解释: 从 1 到 3 ,只有第一栋建筑的平均高度为 2 / 1 = 2。 从 3 到 4 ,第一和第二栋建筑的平均高度均为(2+4)/ 2 = 3。 从 4 到 9 ,只有第二栋建筑的平均高度为 4 / 1 = 4。
示例 2:
输入: buildings = [[1,3,2],[2,5,3],[2,8,3]] 输出: [[1,3,2],[3,8,3]] 解释: 从 1 到 2 ,只有第一栋建筑的平均高度为 2 / 1 = 2。 从 2 到 3 ,这三座建筑的平均高度均为 (2+3+3) / 3 = 2。 从 3 到 5 ,第二和第三栋楼都在那里,平均高度为 (3+3) / 2 = 3。 从 5 到 8 ,只有最后一栋建筑的平均高度为 3 / 1 = 3。 从 1 到 3 的平均高度是相同的,所以我们可以把它们分成一个部分。 从 3 到 8 的平均高度是相同的,所以我们可以把它们分成一个部分。
示例 3:
输入: buildings = [[1,2,1],[5,6,1]] 输出: [[1,2,1],[5,6,1]] 解释: 从 1 到 2 ,只有第一栋建筑的平均高度为 1 / 1 = 1。 从 2 到 5 ,没有建筑物,因此不包括在输出中。 从 5 到 6 ,只有第二栋建筑的平均高度为 1 / 1 = 1。 我们无法将这些部分组合在一起,因为没有建筑的空白空间将这些部分隔开。
提示:
1 <= buildings.length <= 105buildings[i].length == 30 <= starti < endi <= 1081 <= heighti <= 105
我们可以利用差分思想,用一个哈希表
接下来,我们对哈希表
然后遍历哈希表
最后返回结果集即可。
时间复杂度
class Solution:
def averageHeightOfBuildings(self, buildings: List[List[int]]) -> List[List[int]]:
cnt = defaultdict(int)
d = defaultdict(int)
for start, end, height in buildings:
cnt[start] += 1
cnt[end] -= 1
d[start] += height
d[end] -= height
s = m = 0
last = -1
ans = []
for k, v in sorted(d.items()):
if m:
avg = s // m
if ans and ans[-1][2] == avg and ans[-1][1] == last:
ans[-1][1] = k
else:
ans.append([last, k, avg])
s += v
m += cnt[k]
last = k
return ansclass Solution {
public int[][] averageHeightOfBuildings(int[][] buildings) {
Map<Integer, Integer> cnt = new HashMap<>();
TreeMap<Integer, Integer> d = new TreeMap<>();
for (var e : buildings) {
int start = e[0], end = e[1], height = e[2];
cnt.merge(start, 1, Integer::sum);
cnt.merge(end, -1, Integer::sum);
d.merge(start, height, Integer::sum);
d.merge(end, -height, Integer::sum);
}
int s = 0, m = 0;
int last = -1;
List<int[]> ans = new ArrayList<>();
for (var e : d.entrySet()) {
int k = e.getKey(), v = e.getValue();
if (m > 0) {
int avg = s / m;
if (!ans.isEmpty() && ans.get(ans.size() - 1)[2] == avg
&& ans.get(ans.size() - 1)[1] == last) {
ans.get(ans.size() - 1)[1] = k;
} else {
ans.add(new int[] {last, k, avg});
}
}
s += v;
m += cnt.get(k);
last = k;
}
return ans.toArray(new int[0][]);
}
}class Solution {
public:
vector<vector<int>> averageHeightOfBuildings(vector<vector<int>>& buildings) {
unordered_map<int, int> cnt;
map<int, int> d;
for (const auto& e : buildings) {
int start = e[0], end = e[1], height = e[2];
cnt[start]++;
cnt[end]--;
d[start] += height;
d[end] -= height;
}
int s = 0, m = 0;
int last = -1;
vector<vector<int>> ans;
for (const auto& [k, v] : d) {
if (m > 0) {
int avg = s / m;
if (!ans.empty() && ans.back()[2] == avg && ans.back()[1] == last) {
ans.back()[1] = k;
} else {
ans.push_back({last, k, avg});
}
}
s += v;
m += cnt[k];
last = k;
}
return ans;
}
};func averageHeightOfBuildings(buildings [][]int) [][]int {
cnt := make(map[int]int)
d := make(map[int]int)
for _, e := range buildings {
start, end, height := e[0], e[1], e[2]
cnt[start]++
cnt[end]--
d[start] += height
d[end] -= height
}
s, m := 0, 0
last := -1
var ans [][]int
keys := make([]int, 0, len(d))
for k := range d {
keys = append(keys, k)
}
sort.Ints(keys)
for _, k := range keys {
v := d[k]
if m > 0 {
avg := s / m
if len(ans) > 0 && ans[len(ans)-1][2] == avg && ans[len(ans)-1][1] == last {
ans[len(ans)-1][1] = k
} else {
ans = append(ans, []int{last, k, avg})
}
}
s += v
m += cnt[k]
last = k
}
return ans
}function averageHeightOfBuildings(buildings: number[][]): number[][] {
const cnt = new Map<number, number>();
const d = new Map<number, number>();
for (const [start, end, height] of buildings) {
cnt.set(start, (cnt.get(start) || 0) + 1);
cnt.set(end, (cnt.get(end) || 0) - 1);
d.set(start, (d.get(start) || 0) + height);
d.set(end, (d.get(end) || 0) - height);
}
let [s, m] = [0, 0];
let last = -1;
const ans: number[][] = [];
const sortedKeys = Array.from(d.keys()).sort((a, b) => a - b);
for (const k of sortedKeys) {
const v = d.get(k)!;
if (m > 0) {
const avg = Math.floor(s / m);
if (ans.length > 0 && ans.at(-1)![2] === avg && ans.at(-1)![1] === last) {
ans[ans.length - 1][1] = k;
} else {
ans.push([last, k, avg]);
}
}
s += v;
m += cnt.get(k)!;
last = k;
}
return ans;
}