README_EN.md

comments	difficulty	edit_url	rating	source	tags
true	Easy	https://github.com/doocs/leetcode/edit/main/solution/2100-2199/2133.Check%20if%20Every%20Row%20and%20Column%20Contains%20All%20Numbers/README_EN.md	1264	Weekly Contest 275 Q1	Array Hash Table Matrix

2133. Check if Every Row and Column Contains All Numbers

中文文档

Description

An n x n matrix is valid if every row and every column contains all the integers from 1 to n (inclusive).

Given an n x n integer matrix matrix, return true if the matrix is valid. Otherwise, return false.

 

Example 1:

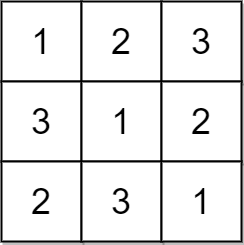
Input: matrix = [[1,2,3],[3,1,2],[2,3,1]]
Output: true
Explanation: In this case, n = 3, and every row and column contains the numbers 1, 2, and 3.
Hence, we return true.

Example 2:

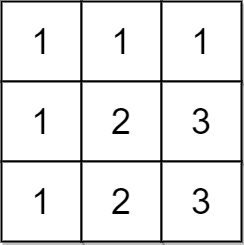
Input: matrix = [[1,1,1],[1,2,3],[1,2,3]]
Output: false
Explanation: In this case, n = 3, but the first row and the first column do not contain the numbers 2 or 3.
Hence, we return false.

 

Constraints:

• n == matrix.length == matrix[i].length
• 1 <= n <= 100
• 1 <= matrix[i][j] <= n

Solutions

Solution 1: Hash Table

Traverse each row and column of the matrix, using a hash table to record whether each number has appeared. If any number appears more than once in a row or column, return false; otherwise, return true

The time complexity is $O(n^2)$, and the space complexity is $O(n)$. Here, $n$ is the size of the matrix.

Python3

class Solution:
    def checkValid(self, matrix: List[List[int]]) -> bool:
        n = len(matrix)
        return all(len(set(row)) == n for row in chain(matrix, zip(*matrix)))

Java

class Solution {
    public boolean checkValid(int[][] matrix) {
        int n = matrix.length;
        boolean[] vis = new boolean[n + 1];
        for (var row : matrix) {
            Arrays.fill(vis, false);
            for (int x : row) {
                if (vis[x]) {
                    return false;
                }
                vis[x] = true;
            }
        }
        for (int j = 0; j < n; ++j) {
            Arrays.fill(vis, false);
            for (int i = 0; i < n; ++i) {
                if (vis[matrix[i][j]]) {
                    return false;
                }
                vis[matrix[i][j]] = true;
            }
        }
        return true;
    }
}

C++

class Solution {
public:
    bool checkValid(vector<vector<int>>& matrix) {
        int n = matrix.size();
        bool vis[n + 1];
        for (const auto& row : matrix) {
            memset(vis, false, sizeof(vis));
            for (int x : row) {
                if (vis[x]) {
                    return false;
                }
                vis[x] = true;
            }
        }
        for (int j = 0; j < n; ++j) {
            memset(vis, false, sizeof(vis));
            for (int i = 0; i < n; ++i) {
                if (vis[matrix[i][j]]) {
                    return false;
                }
                vis[matrix[i][j]] = true;
            }
        }
        return true;
    }
};

Go

func checkValid(matrix [][]int) bool {
	n := len(matrix)
	for _, row := range matrix {
		vis := make([]bool, n+1)
		for _, x := range row {
			if vis[x] {
				return false
			}
			vis[x] = true
		}
	}
	for j := 0; j < n; j++ {
		vis := make([]bool, n+1)
		for i := 0; i < n; i++ {
			if vis[matrix[i][j]] {
				return false
			}
			vis[matrix[i][j]] = true
		}
	}
	return true
}

TypeScript

function checkValid(matrix: number[][]): boolean {
    const n = matrix.length;
    const vis: boolean[] = Array(n + 1).fill(false);
    for (const row of matrix) {
        vis.fill(false);
        for (const x of row) {
            if (vis[x]) {
                return false;
            }
            vis[x] = true;
        }
    }
    for (let j = 0; j < n; ++j) {
        vis.fill(false);
        for (let i = 0; i < n; ++i) {
            if (vis[matrix[i][j]]) {
                return false;
            }
            vis[matrix[i][j]] = true;
        }
    }
    return true;
}