README_EN.md

comments	difficulty	edit_url	rating	source	tags
true	Hard	https://github.com/doocs/leetcode/edit/main/solution/2200-2299/2246.Longest%20Path%20With%20Different%20Adjacent%20Characters/README_EN.md	2126	Weekly Contest 289 Q4	Tree Depth-First Search Graph Topological Sort Array String

2246. Longest Path With Different Adjacent Characters

中文文档

Description

You are given a tree (i.e. a connected, undirected graph that has no cycles) rooted at node 0 consisting of n nodes numbered from 0 to n - 1. The tree is represented by a 0-indexed array parent of size n, where parent[i] is the parent of node i. Since node 0 is the root, parent[0] == -1.

You are also given a string s of length n, where s[i] is the character assigned to node i.

Return the length of the longest path in the tree such that no pair of adjacent nodes on the path have the same character assigned to them.

 

Example 1:

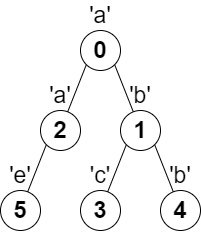
Input: parent = [-1,0,0,1,1,2], s = "abacbe"
Output: 3
Explanation: The longest path where each two adjacent nodes have different characters in the tree is the path: 0 -> 1 -> 3. The length of this path is 3, so 3 is returned.
It can be proven that there is no longer path that satisfies the conditions. 

Example 2:

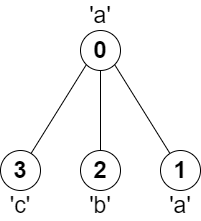
Input: parent = [-1,0,0,0], s = "aabc"
Output: 3
Explanation: The longest path where each two adjacent nodes have different characters is the path: 2 -> 0 -> 3. The length of this path is 3, so 3 is returned.

 

Constraints:

• n == parent.length == s.length
• 1 <= n <= 105
• 0 <= parent[i] <= n - 1 for all i >= 1
• parent[0] == -1
• parent represents a valid tree.
• s consists of only lowercase English letters.

Solutions

Solution 1: Tree-shaped DP

First, we construct an adjacency list $g$ based on the array $parent$, where $g[i]$ represents all child nodes of node $i$.

Then we start DFS from the root node. For each node $i$, we traverse each child node $j$ in $g[i]$. If $s[i] \neq s[j]$, then we can start from node $i$, pass through node $j$, and reach a leaf node. The length of this path is $x = 1 + \textit{dfs}(j)$. We use $mx$ to record the longest path length starting from node $i$. At the same time, we update the answer $ans = \max(ans, mx + x)$ during the traversal process.

Finally, we return $ans + 1$.

The time complexity is $O(n)$, and the space complexity is $O(n)$, where $n$ is the number of nodes.

Python3

class Solution:
    def longestPath(self, parent: List[int], s: str) -> int:
        def dfs(i: int) -> int:
            mx = 0
            nonlocal ans
            for j in g[i]:
                x = dfs(j) + 1
                if s[i] != s[j]:
                    ans = max(ans, mx + x)
                    mx = max(mx, x)
            return mx

        g = defaultdict(list)
        for i in range(1, len(parent)):
            g[parent[i]].append(i)
        ans = 0
        dfs(0)
        return ans + 1

Java

class Solution {
    private List<Integer>[] g;
    private String s;
    private int ans;

    public int longestPath(int[] parent, String s) {
        int n = parent.length;
        g = new List[n];
        this.s = s;
        Arrays.setAll(g, k -> new ArrayList<>());
        for (int i = 1; i < n; ++i) {
            g[parent[i]].add(i);
        }
        dfs(0);
        return ans + 1;
    }

    private int dfs(int i) {
        int mx = 0;
        for (int j : g[i]) {
            int x = dfs(j) + 1;
            if (s.charAt(i) != s.charAt(j)) {
                ans = Math.max(ans, mx + x);
                mx = Math.max(mx, x);
            }
        }
        return mx;
    }
}

C++

class Solution {
public:
    int longestPath(vector<int>& parent, string s) {
        int n = parent.size();
        vector<int> g[n];
        for (int i = 1; i < n; ++i) {
            g[parent[i]].push_back(i);
        }
        int ans = 0;
        function<int(int)> dfs = [&](int i) -> int {
            int mx = 0;
            for (int j : g[i]) {
                int x = dfs(j) + 1;
                if (s[i] != s[j]) {
                    ans = max(ans, mx + x);
                    mx = max(mx, x);
                }
            }
            return mx;
        };
        dfs(0);
        return ans + 1;
    }
};

Go

func longestPath(parent []int, s string) int {
	n := len(parent)
	g := make([][]int, n)
	for i := 1; i < n; i++ {
		g[parent[i]] = append(g[parent[i]], i)
	}
	ans := 0
	var dfs func(int) int
	dfs = func(i int) int {
		mx := 0
		for _, j := range g[i] {
			x := dfs(j) + 1
			if s[i] != s[j] {
				ans = max(ans, x+mx)
				mx = max(mx, x)
			}
		}
		return mx
	}
	dfs(0)
	return ans + 1
}

TypeScript

function longestPath(parent: number[], s: string): number {
    const n = parent.length;
    const g: number[][] = Array.from({ length: n }, () => []);
    for (let i = 1; i < n; ++i) {
        g[parent[i]].push(i);
    }
    let ans = 0;
    const dfs = (i: number): number => {
        let mx = 0;
        for (const j of g[i]) {
            const x = dfs(j) + 1;
            if (s[i] !== s[j]) {
                ans = Math.max(ans, mx + x);
                mx = Math.max(mx, x);
            }
        }
        return mx;
    };
    dfs(0);
    return ans + 1;
}