README_EN.md

comments	difficulty	edit_url	rating	source	tags
true	Medium	https://github.com/doocs/leetcode/edit/main/solution/2200-2299/2265.Count%20Nodes%20Equal%20to%20Average%20of%20Subtree/README_EN.md	1472	Weekly Contest 292 Q2	Tree Depth-First Search Binary Tree

2265. Count Nodes Equal to Average of Subtree

中文文档

Description

Given the root of a binary tree, return the number of nodes where the value of the node is equal to the average of the values in its subtree.

Note:

• The average of n elements is the sum of the n elements divided by n and rounded down to the nearest integer.
• A subtree of root is a tree consisting of root and all of its descendants.

 

Example 1:

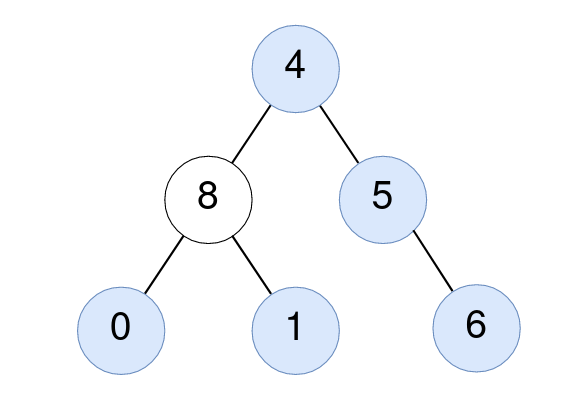
Input: root = [4,8,5,0,1,null,6]
Output: 5
Explanation: 
For the node with value 4: The average of its subtree is (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4.
For the node with value 5: The average of its subtree is (5 + 6) / 2 = 11 / 2 = 5.
For the node with value 0: The average of its subtree is 0 / 1 = 0.
For the node with value 1: The average of its subtree is 1 / 1 = 1.
For the node with value 6: The average of its subtree is 6 / 1 = 6.

Example 2:

Input: root = [1]
Output: 1
Explanation: For the node with value 1: The average of its subtree is 1 / 1 = 1.

 

Constraints:

• The number of nodes in the tree is in the range [1, 1000].
• 0 <= Node.val <= 1000

Solutions

Solution 1: DFS

We design a function $\textit{dfs}$, which calculates the sum and the number of nodes of the subtree rooted at the current node.

The execution process of the function $\textit{dfs}$ is as follows:

• If the current node is null, return $(0, 0)$.
• Otherwise, we recursively calculate the sum and the number of nodes of the left and right subtrees, denoted as $(\textit{ls}, \textit{ln})$ and $(\textit{rs}, \textit{rn})$, respectively. Then, the sum $\textit{s}$ and the number of nodes $\textit{n}$ of the subtree rooted at the current node are $\textit{ls} + \textit{rs} + \textit{root.val}$ and $\textit{ln} + \textit{rn} + 1$, respectively. If $\textit{s} / \textit{n} = \textit{root.val}$, it means the current node meets the requirement of the problem, and we increment the answer $\textit{ans}$ by $1$.
• Finally, the function $\textit{dfs}$ returns $\textit{s}$ and $\textit{n}$.

We initialize the answer $\textit{ans}$ to $0$, then call the $\textit{dfs}$ function, and finally return the answer $\textit{ans}$.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ represents the number of nodes in the binary tree.

Python3

class Solution:
    def averageOfSubtree(self, root: TreeNode) -> int:
        def dfs(root) -> tuple:
            if not root:
                return 0, 0
            ls, ln = dfs(root.left)
            rs, rn = dfs(root.right)
            s = ls + rs + root.val
            n = ln + rn + 1
            nonlocal ans
            ans += int(s // n == root.val)
            return s, n

        ans = 0
        dfs(root)
        return ans

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int ans;

    public int averageOfSubtree(TreeNode root) {
        dfs(root);
        return ans;
    }

    private int[] dfs(TreeNode root) {
        if (root == null) {
            return new int[2];
        }
        var l = dfs(root.left);
        var r = dfs(root.right);
        int s = l[0] + r[0] + root.val;
        int n = l[1] + r[1] + 1;
        if (s / n == root.val) {
            ++ans;
        }
        return new int[] {s, n};
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int averageOfSubtree(TreeNode* root) {
        int ans = 0;
        auto dfs = [&](auto&& dfs, TreeNode* root) -> pair<int, int> {
            if (!root) {
                return {0, 0};
            }
            auto [ls, ln] = dfs(dfs, root->left);
            auto [rs, rn] = dfs(dfs, root->right);
            int s = ls + rs + root->val;
            int n = ln + rn + 1;
            if (s / n == root->val) {
                ++ans;
            }
            return {s, n};
        };
        dfs(dfs, root);
        return ans;
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func averageOfSubtree(root *TreeNode) (ans int) {
	var dfs func(root *TreeNode) (int, int)
	dfs = func(root *TreeNode) (int, int) {
		if root == nil {
			return 0, 0
		}
		ls, ln := dfs(root.Left)
		rs, rn := dfs(root.Right)
		s, n := ls+rs+root.Val, ln+rn+1
		if s/n == root.Val {
			ans++
		}
		return s, n
	}
	dfs(root)
	return
}

TypeScript

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function averageOfSubtree(root: TreeNode | null): number {
    let ans: number = 0;
    const dfs = (root: TreeNode | null): [number, number] => {
        if (!root) {
            return [0, 0];
        }
        const [ls, ln] = dfs(root.left);
        const [rs, rn] = dfs(root.right);
        const s = ls + rs + root.val;
        const n = ln + rn + 1;
        if (Math.floor(s / n) === root.val) {
            ++ans;
        }
        return [s, n];
    };
    dfs(root);
    return ans;
}