| comments | difficulty | edit_url | rating | source | tags | |||
|---|---|---|---|---|---|---|---|---|
true |
Hard |
2415 |
Weekly Contest 322 Q4 |
|
You are given a positive integer n representing the number of nodes in an undirected graph. The nodes are labeled from 1 to n.
You are also given a 2D integer array edges, where edges[i] = [ai, bi] indicates that there is a bidirectional edge between nodes ai and bi. Notice that the given graph may be disconnected.
Divide the nodes of the graph into m groups (1-indexed) such that:
- Each node in the graph belongs to exactly one group.
- For every pair of nodes in the graph that are connected by an edge
[ai, bi], ifaibelongs to the group with indexx, andbibelongs to the group with indexy, then|y - x| = 1.
Return the maximum number of groups (i.e., maximum m) into which you can divide the nodes. Return -1 if it is impossible to group the nodes with the given conditions.
Example 1:
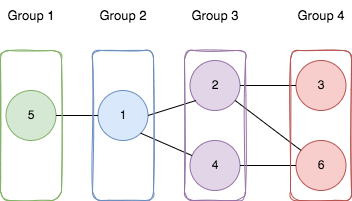
Input: n = 6, edges = [[1,2],[1,4],[1,5],[2,6],[2,3],[4,6]] Output: 4 Explanation: As shown in the image we: - Add node 5 to the first group. - Add node 1 to the second group. - Add nodes 2 and 4 to the third group. - Add nodes 3 and 6 to the fourth group. We can see that every edge is satisfied. It can be shown that that if we create a fifth group and move any node from the third or fourth group to it, at least on of the edges will not be satisfied.
Example 2:
Input: n = 3, edges = [[1,2],[2,3],[3,1]] Output: -1 Explanation: If we add node 1 to the first group, node 2 to the second group, and node 3 to the third group to satisfy the first two edges, we can see that the third edge will not be satisfied. It can be shown that no grouping is possible.
Constraints:
1 <= n <= 5001 <= edges.length <= 104edges[i].length == 21 <= ai, bi <= nai != bi- There is at most one edge between any pair of vertices.
Given that the graph provided by the problem may be disconnected, we need to process each connected component, find the maximum number of groups in each connected component, and accumulate them to get the final result.
We can enumerate each node as the node of the first group, then use BFS to traverse the entire connected component, and use an array
During the BFS process, we use a queue
During the traversal, if we find that the
The time complexity is
class Solution:
def magnificentSets(self, n: int, edges: List[List[int]]) -> int:
g = [[] for _ in range(n)]
for a, b in edges:
g[a - 1].append(b - 1)
g[b - 1].append(a - 1)
d = defaultdict(int)
for i in range(n):
q = deque([i])
dist = [0] * n
dist[i] = mx = 1
root = i
while q:
a = q.popleft()
root = min(root, a)
for b in g[a]:
if dist[b] == 0:
dist[b] = dist[a] + 1
mx = max(mx, dist[b])
q.append(b)
elif abs(dist[b] - dist[a]) != 1:
return -1
d[root] = max(d[root], mx)
return sum(d.values())class Solution {
public int magnificentSets(int n, int[][] edges) {
List<Integer>[] g = new List[n];
Arrays.setAll(g, k -> new ArrayList<>());
for (var e : edges) {
int a = e[0] - 1, b = e[1] - 1;
g[a].add(b);
g[b].add(a);
}
int[] d = new int[n];
int[] dist = new int[n];
for (int i = 0; i < n; ++i) {
Deque<Integer> q = new ArrayDeque<>();
q.offer(i);
Arrays.fill(dist, 0);
dist[i] = 1;
int mx = 1;
int root = i;
while (!q.isEmpty()) {
int a = q.poll();
root = Math.min(root, a);
for (int b : g[a]) {
if (dist[b] == 0) {
dist[b] = dist[a] + 1;
mx = Math.max(mx, dist[b]);
q.offer(b);
} else if (Math.abs(dist[b] - dist[a]) != 1) {
return -1;
}
}
}
d[root] = Math.max(d[root], mx);
}
return Arrays.stream(d).sum();
}
}class Solution {
public:
int magnificentSets(int n, vector<vector<int>>& edges) {
vector<int> g[n];
for (auto& e : edges) {
int a = e[0] - 1, b = e[1] - 1;
g[a].push_back(b);
g[b].push_back(a);
}
vector<int> d(n);
for (int i = 0; i < n; ++i) {
queue<int> q{{i}};
vector<int> dist(n);
dist[i] = 1;
int mx = 1;
int root = i;
while (q.size()) {
int a = q.front();
q.pop();
root = min(root, a);
for (int b : g[a]) {
if (dist[b] == 0) {
dist[b] = dist[a] + 1;
mx = max(mx, dist[b]);
q.push(b);
} else if (abs(dist[b] - dist[a]) != 1) {
return -1;
}
}
}
d[root] = max(d[root], mx);
}
return accumulate(d.begin(), d.end(), 0);
}
};func magnificentSets(n int, edges [][]int) (ans int) {
g := make([][]int, n)
for _, e := range edges {
a, b := e[0]-1, e[1]-1
g[a] = append(g[a], b)
g[b] = append(g[b], a)
}
d := make([]int, n)
for i := range d {
q := []int{i}
dist := make([]int, n)
dist[i] = 1
mx := 1
root := i
for len(q) > 0 {
a := q[0]
q = q[1:]
root = min(root, a)
for _, b := range g[a] {
if dist[b] == 0 {
dist[b] = dist[a] + 1
mx = max(mx, dist[b])
q = append(q, b)
} else if abs(dist[b]-dist[a]) != 1 {
return -1
}
}
}
d[root] = max(d[root], mx)
}
for _, x := range d {
ans += x
}
return
}
func abs(x int) int {
if x < 0 {
return -x
}
return x
}/**
* @param {number} n
* @param {number[][]} edges
* @return {number}
*/
var magnificentSets = function (n, edges) {
const g = Array.from({ length: n }, () => []);
for (const [a, b] of edges) {
g[a - 1].push(b - 1);
g[b - 1].push(a - 1);
}
const d = Array(n).fill(0);
for (let i = 0; i < n; ++i) {
const q = [i];
const dist = Array(n).fill(0);
dist[i] = 1;
let mx = 1;
let root = i;
while (q.length) {
const a = q.shift();
root = Math.min(root, a);
for (const b of g[a]) {
if (dist[b] === 0) {
dist[b] = dist[a] + 1;
mx = Math.max(mx, dist[b]);
q.push(b);
} else if (Math.abs(dist[b] - dist[a]) !== 1) {
return -1;
}
}
}
d[root] = Math.max(d[root], mx);
}
return d.reduce((a, b) => a + b);
};