| comments | difficulty | edit_url | tags | ||||
|---|---|---|---|---|---|---|---|
true |
Medium |
|
You are given a root, which is the root of a special binary tree with n nodes. The nodes of the special binary tree are numbered from 1 to n. Suppose the tree has k leaves in the following order: b1 < b2 < ... < bk.
The leaves of this tree have a special property! That is, for every leaf bi, the following conditions hold:
- The right child of
biisbi + 1ifi < k, andb1otherwise. - The left child of
biisbi - 1ifi > 1, andbkotherwise.
Return the height of the given tree.
Note: The height of a binary tree is the length of the longest path from the root to any other node.
Example 1:
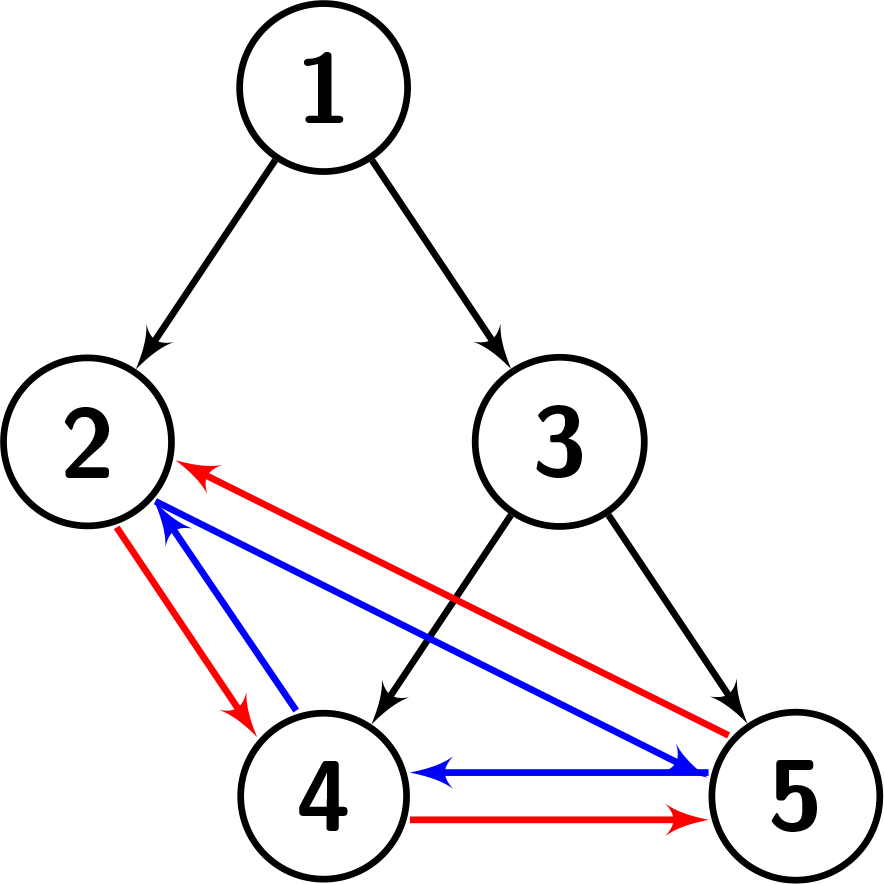
Input: root = [1,2,3,null,null,4,5] Output: 2 Explanation: The given tree is shown in the following picture. Each leaf's left child is the leaf to its left (shown with the blue edges). Each leaf's right child is the leaf to its right (shown with the red edges). We can see that the graph has a height of 2.
Example 2:
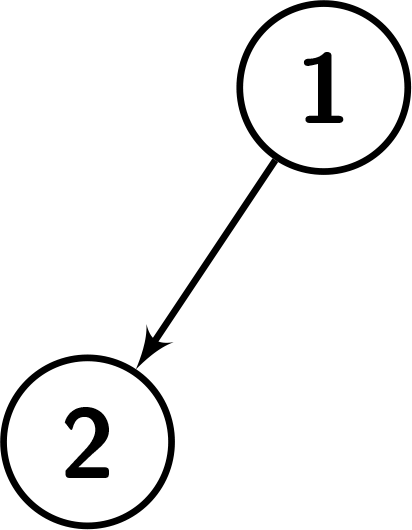
Input: root = [1,2] Output: 1 Explanation: The given tree is shown in the following picture. There is only one leaf, so it doesn't have any left or right child. We can see that the graph has a height of 1.
Example 3:
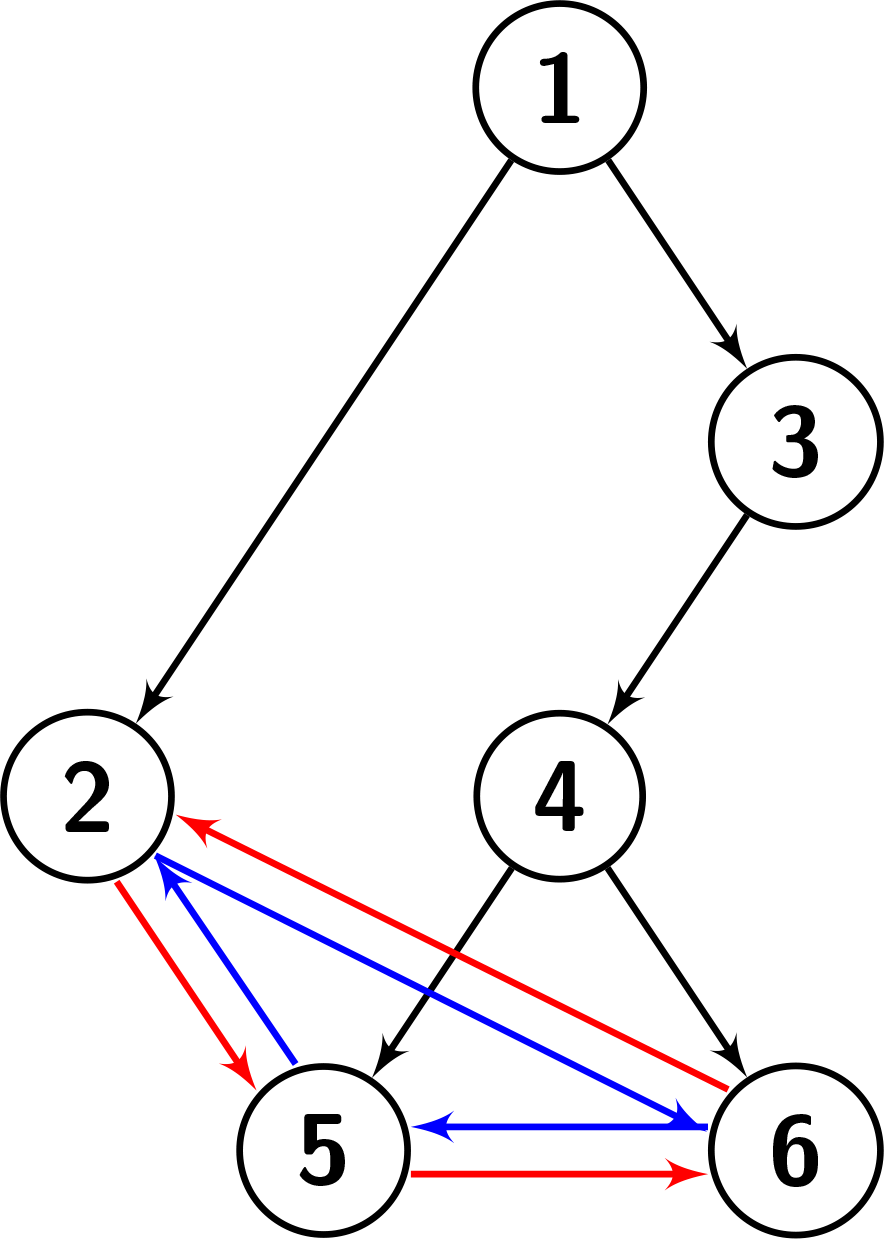
Input: root = [1,2,3,null,null,4,null,5,6] Output: 3 Explanation: The given tree is shown in the following picture. Each leaf's left child is the leaf to its left (shown with the blue edges). Each leaf's right child is the leaf to its right (shown with the red edges). We can see that the graph has a height of 3.
Constraints:
n == number of nodes in the tree2 <= n <= 1041 <= node.val <= n- The input is generated such that each
node.valis unique.
The key to the problem is how to determine whether a node is a leaf node. We design a function
The time complexity is
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def heightOfTree(self, root: Optional[TreeNode]) -> int:
def dfs(root: Optional[TreeNode], d: int):
nonlocal ans
ans = max(ans, d)
if root.left and root.left.right != root:
dfs(root.left, d + 1)
if root.right and root.right.left != root:
dfs(root.right, d + 1)
ans = 0
dfs(root, 0)
return ans/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private int ans;
public int heightOfTree(TreeNode root) {
dfs(root, 0);
return ans;
}
private void dfs(TreeNode root, int d) {
ans = Math.max(ans, d++);
if (root.left != null && root.left.right != root) {
dfs(root.left, d);
}
if (root.right != null && root.right.left != root) {
dfs(root.right, d);
}
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int heightOfTree(TreeNode* root) {
int ans = 0;
function<void(TreeNode*, int)> dfs = [&](TreeNode* root, int d) {
ans = max(ans, d++);
if (root->left && root->left->right != root) {
dfs(root->left, d);
}
if (root->right && root->right->left != root) {
dfs(root->right, d);
}
};
dfs(root, 0);
return ans;
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func heightOfTree(root *TreeNode) (ans int) {
var dfs func(*TreeNode, int)
dfs = func(root *TreeNode, d int) {
if ans < d {
ans = d
}
d++
if root.Left != nil && root.Left.Right != root {
dfs(root.Left, d)
}
if root.Right != nil && root.Right.Left != root {
dfs(root.Right, d)
}
}
dfs(root, 0)
return
}/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function heightOfTree(root: TreeNode | null): number {
let ans = 0;
const dfs = (root: TreeNode | null, d: number) => {
ans = Math.max(ans, d++);
if (root.left && root.left.right !== root) {
dfs(root.left, d);
}
if (root.right && root.right.left !== root) {
dfs(root.right, d);
}
};
dfs(root, 0);
return ans;
}