| comments | difficulty | edit_url | rating | source | tags | ||||
|---|---|---|---|---|---|---|---|---|---|
true |
Easy |
1405 |
Weekly Contest 373 Q1 |
|
You are given an m x n integer matrix mat and an integer k. The matrix rows are 0-indexed.
The following proccess happens k times:
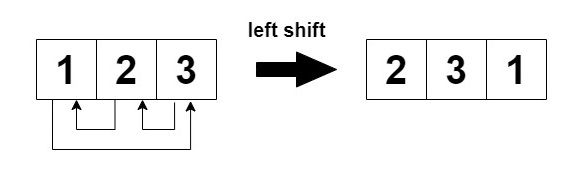
- Even-indexed rows (0, 2, 4, ...) are cyclically shifted to the left.
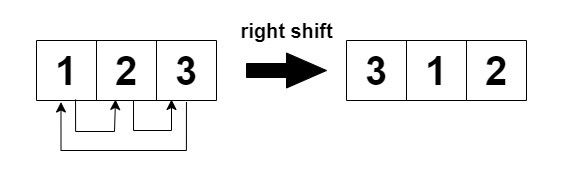
- Odd-indexed rows (1, 3, 5, ...) are cyclically shifted to the right.
Return true if the final modified matrix after k steps is identical to the original matrix, and false otherwise.
Example 1:
Input: mat = [[1,2,3],[4,5,6],[7,8,9]], k = 4
Output: false
Explanation:
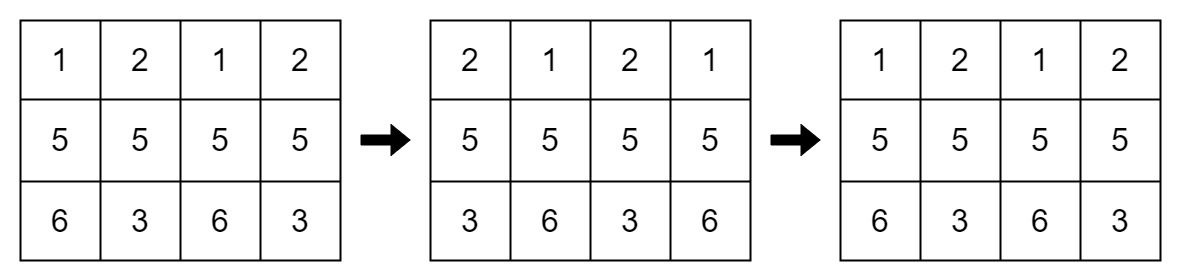
In each step left shift is applied to rows 0 and 2 (even indices), and right shift to row 1 (odd index).
Example 2:
Example 3:
Input: mat = [[2,2],[2,2]], k = 3
Output: true
Explanation:
As all the values are equal in the matrix, even after performing cyclic shifts the matrix will remain the same.
Constraints:
1 <= mat.length <= 251 <= mat[i].length <= 251 <= mat[i][j] <= 251 <= k <= 50
class Solution:
def areSimilar(self, mat: List[List[int]], k: int) -> bool:
n = len(mat[0])
for i, row in enumerate(mat):
for j, x in enumerate(row):
if i % 2 == 1 and x != mat[i][(j + k) % n]:
return False
if i % 2 == 0 and x != mat[i][(j - k + n) % n]:
return False
return Trueclass Solution {
public boolean areSimilar(int[][] mat, int k) {
int m = mat.length, n = mat[0].length;
k %= n;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (i % 2 == 1 && mat[i][j] != mat[i][(j + k) % n]) {
return false;
}
if (i % 2 == 0 && mat[i][j] != mat[i][(j - k + n) % n]) {
return false;
}
}
}
return true;
}
}class Solution {
public:
bool areSimilar(vector<vector<int>>& mat, int k) {
int m = mat.size(), n = mat[0].size();
k %= n;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (i % 2 == 1 && mat[i][j] != mat[i][(j + k) % n]) {
return false;
}
if (i % 2 == 0 && mat[i][j] != mat[i][(j - k + n) % n]) {
return false;
}
}
}
return true;
}
};func areSimilar(mat [][]int, k int) bool {
n := len(mat[0])
k %= n
for i, row := range mat {
for j, x := range row {
if i%2 == 1 && x != mat[i][(j+k)%n] {
return false
}
if i%2 == 0 && x != mat[i][(j-k+n)%n] {
return false
}
}
}
return true
}function areSimilar(mat: number[][], k: number): boolean {
const m = mat.length;
const n = mat[0].length;
k %= n;
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
if (i % 2 === 1 && mat[i][j] !== mat[i][(j + k) % n]) {
return false;
}
if (i % 2 === 0 && mat[i][j] !== mat[i][(j - k + n) % n]) {
return false;
}
}
}
return true;
}