README_EN.md

comments	difficulty	edit_url	rating	source	tags
true	Easy	https://github.com/doocs/leetcode/edit/main/solution/2900-2999/2956.Find%20Common%20Elements%20Between%20Two%20Arrays/README_EN.md	1214	Biweekly Contest 119 Q1	Array Hash Table

2956. Find Common Elements Between Two Arrays

中文文档

Description

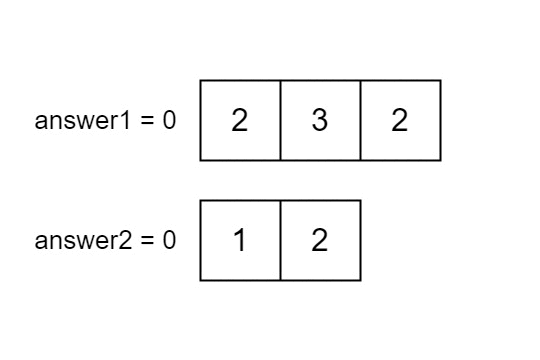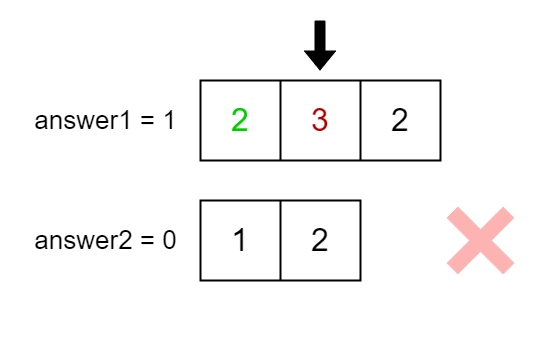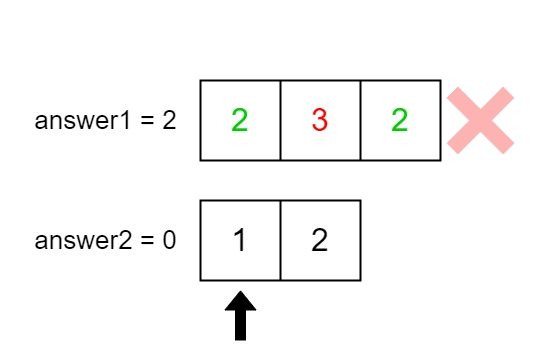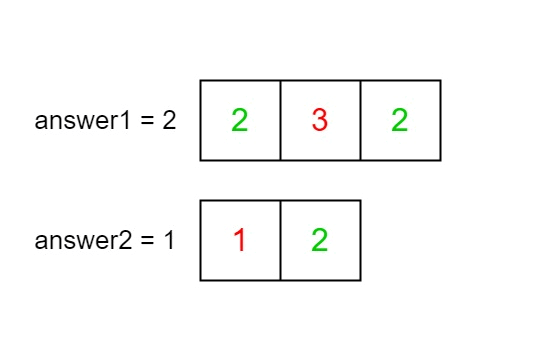
You are given two integer arrays nums1 and nums2 of sizes n and m, respectively. Calculate the following values:

• answer1 : the number of indices i such that nums1[i] exists in nums2.
• answer2 : the number of indices i such that nums2[i] exists in nums1.

Return [answer1,answer2].

 

Example 1:

Input: nums1 = [2,3,2], nums2 = [1,2]

Output: [2,1]

Explanation:

Example 2:

Input: nums1 = [4,3,2,3,1], nums2 = [2,2,5,2,3,6]

Output: [3,4]

Explanation:

The elements at indices 1, 2, and 3 in nums1 exist in nums2 as well. So answer1 is 3.

The elements at indices 0, 1, 3, and 4 in nums2 exist in nums1. So answer2 is 4.

Example 3:

Input: nums1 = [3,4,2,3], nums2 = [1,5]

Output: [0,0]

Explanation:

No numbers are common between nums1 and nums2, so answer is [0,0].

 

Constraints:

• n == nums1.length
• m == nums2.length
• 1 <= n, m <= 100
• 1 <= nums1[i], nums2[i] <= 100

Solutions

Solution 1: Hash Table or Array

We can use two hash tables or arrays $s1$ and $s2$ to record the elements that appear in the two arrays respectively.

Next, we create an array $ans$ of length $2$, where $ans[0]$ represents the number of elements in $nums1$ that appear in $s2$, and $ans[1]$ represents the number of elements in $nums2$ that appear in $s1$.

Then, we traverse each element $x$ in the array $nums1$. If $x$ has appeared in $s2$, we increment $ans[0]$. After that, we traverse each element $x$ in the array $nums2$. If $x$ has appeared in $s1$, we increment $ans[1]$.

Finally, we return the array $ans$.

The time complexity is $O(n + m)$, and the space complexity is $O(n + m)$. Here, $n$ and $m$ are the lengths of the arrays $nums1$ and $nums2$ respectively.

Python3

class Solution:
    def findIntersectionValues(self, nums1: List[int], nums2: List[int]) -> List[int]:
        s1, s2 = set(nums1), set(nums2)
        return [sum(x in s2 for x in nums1), sum(x in s1 for x in nums2)]

Java

class Solution {
    public int[] findIntersectionValues(int[] nums1, int[] nums2) {
        int[] s1 = new int[101];
        int[] s2 = new int[101];
        for (int x : nums1) {
            s1[x] = 1;
        }
        for (int x : nums2) {
            s2[x] = 1;
        }
        int[] ans = new int[2];
        for (int x : nums1) {
            ans[0] += s2[x];
        }
        for (int x : nums2) {
            ans[1] += s1[x];
        }
        return ans;
    }
}

C++

class Solution {
public:
    vector<int> findIntersectionValues(vector<int>& nums1, vector<int>& nums2) {
        int s1[101]{};
        int s2[101]{};
        for (int& x : nums1) {
            s1[x] = 1;
        }
        for (int& x : nums2) {
            s2[x] = 1;
        }
        vector<int> ans(2);
        for (int& x : nums1) {
            ans[0] += s2[x];
        }
        for (int& x : nums2) {
            ans[1] += s1[x];
        }
        return ans;
    }
};

Go

func findIntersectionValues(nums1 []int, nums2 []int) []int {
	s1 := [101]int{}
	s2 := [101]int{}
	for _, x := range nums1 {
		s1[x] = 1
	}
	for _, x := range nums2 {
		s2[x] = 1
	}
	ans := make([]int, 2)
	for _, x := range nums1 {
		ans[0] += s2[x]
	}
	for _, x := range nums2 {
		ans[1] += s1[x]
	}
	return ans
}

TypeScript

function findIntersectionValues(nums1: number[], nums2: number[]): number[] {
    const s1: number[] = Array(101).fill(0);
    const s2: number[] = Array(101).fill(0);
    for (const x of nums1) {
        s1[x] = 1;
    }
    for (const x of nums2) {
        s2[x] = 1;
    }
    const ans: number[] = Array(2).fill(0);
    for (const x of nums1) {
        ans[0] += s2[x];
    }
    for (const x of nums2) {
        ans[1] += s1[x];
    }
    return ans;
}