README_EN.md

comments	difficulty	edit_url	rating	source	tags
true	Medium	https://github.com/doocs/leetcode/edit/main/solution/3100-3199/3122.Minimum%20Number%20of%20Operations%20to%20Satisfy%20Conditions/README_EN.md	1904	Weekly Contest 394 Q3	Array Dynamic Programming Matrix

3122. Minimum Number of Operations to Satisfy Conditions

中文文档

Description

You are given a 2D matrix grid of size m x n. In one operation, you can change the value of any cell to any non-negative number. You need to perform some operations such that each cell grid[i][j] is:

• Equal to the cell below it, i.e. grid[i][j] == grid[i + 1][j] (if it exists).
• Different from the cell to its right, i.e. grid[i][j] != grid[i][j + 1] (if it exists).

Return the minimum number of operations needed.

 

Example 1:

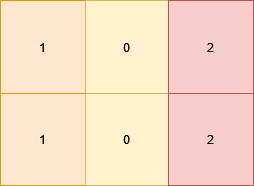
Input: grid = [[1,0,2],[1,0,2]]

Output: 0

Explanation:

All the cells in the matrix already satisfy the properties.

Example 2:

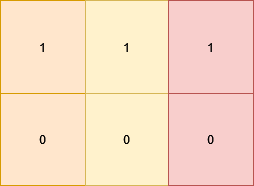
Input: grid = [[1,1,1],[0,0,0]]

Output: 3

Explanation:

The matrix becomes [[1,0,1],[1,0,1]] which satisfies the properties, by doing these 3 operations:

• Change grid[1][0] to 1.
• Change grid[0][1] to 0.
• Change grid[1][2] to 1.

Example 3:

Input: grid = [[1],[2],[3]]

Output: 2

Explanation:

There is a single column. We can change the value to 1 in each cell using 2 operations.

 

Constraints:

• 1 <= n, m <= 1000
• 0 <= grid[i][j] <= 9

Solutions

Solution 1: Dynamic Programming

We notice that the values in the cells of the matrix only have 10 possibilities. The problem requires us to find the minimum number of operations for each column to have the same number, and the numbers in adjacent columns are different. Therefore, we only need to consider the case of modifying the number to 0 to 9.

We define the state $f[i][j]$ to represent the minimum number of operations for the numbers in the first $[0,..i]$ columns, and the number in the $i$-th column is $j$. Then we can get the state transition equation:

$$ f[i][j] = \min_{k \neq j} (f[i-1][k] + m - \textit{cnt}[j]) $$

Where $\textit{cnt}[j]$ represents the number of cells in the $i$-th column that are $j$.

Finally, we only need to find the minimum value of $f[n-1][j]$.

The time complexity is $O(n \times (m + C^2))$, and the space complexity is $O(n \times C)$. Where $m$ and $n$ represent the number of rows and columns in the matrix respectively; and $C$ represents the number of types of numbers, here $C = 10$.

Python3

class Solution:
    def minimumOperations(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        f = [[inf] * 10 for _ in range(n)]
        for i in range(n):
            cnt = [0] * 10
            for j in range(m):
                cnt[grid[j][i]] += 1
            if i == 0:
                for j in range(10):
                    f[i][j] = m - cnt[j]
            else:
                for j in range(10):
                    for k in range(10):
                        if k != j:
                            f[i][j] = min(f[i][j], f[i - 1][k] + m - cnt[j])
        return min(f[-1])

Java

class Solution {
    public int minimumOperations(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        int[][] f = new int[n][10];
        final int inf = 1 << 29;
        for (var g : f) {
            Arrays.fill(g, inf);
        }
        for (int i = 0; i < n; ++i) {
            int[] cnt = new int[10];
            for (int j = 0; j < m; ++j) {
                ++cnt[grid[j][i]];
            }
            if (i == 0) {
                for (int j = 0; j < 10; ++j) {
                    f[i][j] = m - cnt[j];
                }
            } else {
                for (int j = 0; j < 10; ++j) {
                    for (int k = 0; k < 10; ++k) {
                        if (k != j) {
                            f[i][j] = Math.min(f[i][j], f[i - 1][k] + m - cnt[j]);
                        }
                    }
                }
            }
        }
        int ans = inf;
        for (int j = 0; j < 10; ++j) {
            ans = Math.min(ans, f[n - 1][j]);
        }
        return ans;
    }
}

C++

class Solution {
public:
    int minimumOperations(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        int f[n][10];
        memset(f, 0x3f, sizeof(f));
        for (int i = 0; i < n; ++i) {
            int cnt[10]{};
            for (int j = 0; j < m; ++j) {
                ++cnt[grid[j][i]];
            }
            if (i == 0) {
                for (int j = 0; j < 10; ++j) {
                    f[i][j] = m - cnt[j];
                }
            } else {
                for (int j = 0; j < 10; ++j) {
                    for (int k = 0; k < 10; ++k) {
                        if (k != j) {
                            f[i][j] = min(f[i][j], f[i - 1][k] + m - cnt[j]);
                        }
                    }
                }
            }
        }
        return *min_element(f[n - 1], f[n - 1] + 10);
    }
};

Go

func minimumOperations(grid [][]int) int {
	m, n := len(grid), len(grid[0])
	f := make([][]int, n)
	for i := range f {
		f[i] = make([]int, 10)
		for j := range f[i] {
			f[i][j] = 1 << 29
		}
	}
	for i := 0; i < n; i++ {
		cnt := [10]int{}
		for j := 0; j < m; j++ {
			cnt[grid[j][i]]++
		}
		if i == 0 {
			for j := 0; j < 10; j++ {
				f[i][j] = m - cnt[j]
			}
		} else {
			for j := 0; j < 10; j++ {
				for k := 0; k < 10; k++ {
					if j != k {
						f[i][j] = min(f[i][j], f[i-1][k]+m-cnt[j])
					}
				}
			}
		}
	}
	return slices.Min(f[n-1])
}

TypeScript

function minimumOperations(grid: number[][]): number {
    const m = grid.length;
    const n = grid[0].length;
    const f: number[][] = Array.from({ length: n }, () =>
        Array.from({ length: 10 }, () => Infinity),
    );
    for (let i = 0; i < n; ++i) {
        const cnt: number[] = Array(10).fill(0);
        for (let j = 0; j < m; ++j) {
            cnt[grid[j][i]]++;
        }
        if (i === 0) {
            for (let j = 0; j < 10; ++j) {
                f[i][j] = m - cnt[j];
            }
        } else {
            for (let j = 0; j < 10; ++j) {
                for (let k = 0; k < 10; ++k) {
                    if (j !== k) {
                        f[i][j] = Math.min(f[i][j], f[i - 1][k] + m - cnt[j]);
                    }
                }
            }
        }
    }
    return Math.min(...f[n - 1]);
}