| comments | difficulty | edit_url | rating | source | tags | |||
|---|---|---|---|---|---|---|---|---|
true |
中等 |
1710 |
第 418 场周赛 Q2 |
|
你正在维护一个项目,该项目有 n 个方法,编号从 0 到 n - 1。
给你两个整数 n 和 k,以及一个二维整数数组 invocations,其中 invocations[i] = [ai, bi] 表示方法 ai 调用了方法 bi。
已知如果方法 k 存在一个已知的 bug。那么方法 k 以及它直接或间接调用的任何方法都被视为 可疑方法 ,我们需要从项目中移除这些方法。
只有当一组方法没有被这组之外的任何方法调用时,这组方法才能被移除。
返回一个数组,包含移除所有 可疑方法 后剩下的所有方法。你可以以任意顺序返回答案。如果无法移除 所有 可疑方法,则 不 移除任何方法。
示例 1:
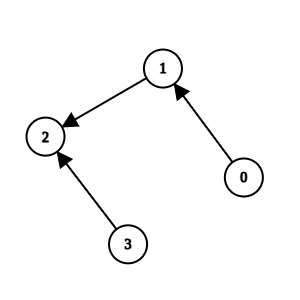
输入: n = 4, k = 1, invocations = [[1,2],[0,1],[3,2]]
输出: [0,1,2,3]
解释:
方法 2 和方法 1 是可疑方法,但它们分别直接被方法 3 和方法 0 调用。由于方法 3 和方法 0 不是可疑方法,我们无法移除任何方法,故返回所有方法。
示例 2:
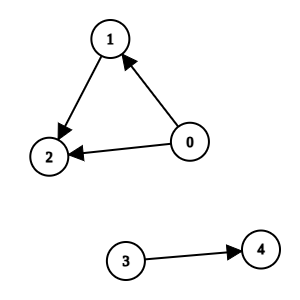
输入: n = 5, k = 0, invocations = [[1,2],[0,2],[0,1],[3,4]]
输出: [3,4]
解释:
方法 0、方法 1 和方法 2 是可疑方法,且没有被任何其他方法直接调用。我们可以移除它们。
示例 3:
提示:
1 <= n <= 1050 <= k <= n - 10 <= invocations.length <= 2 * 105invocations[i] == [ai, bi]0 <= ai, bi <= n - 1ai != biinvocations[i] != invocations[j]
我们可以先从
时间复杂度
class Solution:
def remainingMethods(
self, n: int, k: int, invocations: List[List[int]]
) -> List[int]:
def dfs(i: int):
suspicious[i] = True
for j in g[i]:
if not suspicious[j]:
dfs(j)
def dfs2(i: int):
vis[i] = True
for j in f[i]:
if not vis[j]:
suspicious[j] = False
dfs2(j)
f = [[] for _ in range(n)]
g = [[] for _ in range(n)]
for a, b in invocations:
f[a].append(b)
f[b].append(a)
g[a].append(b)
suspicious = [False] * n
dfs(k)
vis = [False] * n
ans = []
for i in range(n):
if not suspicious[i] and not vis[i]:
dfs2(i)
return [i for i in range(n) if not suspicious[i]]class Solution {
private boolean[] suspicious;
private boolean[] vis;
private List<Integer>[] f;
private List<Integer>[] g;
public List<Integer> remainingMethods(int n, int k, int[][] invocations) {
suspicious = new boolean[n];
vis = new boolean[n];
f = new List[n];
g = new List[n];
Arrays.setAll(f, i -> new ArrayList<>());
Arrays.setAll(g, i -> new ArrayList<>());
for (var e : invocations) {
int a = e[0], b = e[1];
f[a].add(b);
f[b].add(a);
g[a].add(b);
}
dfs(k);
for (int i = 0; i < n; ++i) {
if (!suspicious[i] && !vis[i]) {
dfs2(i);
}
}
List<Integer> ans = new ArrayList<>();
for (int i = 0; i < n; ++i) {
if (!suspicious[i]) {
ans.add(i);
}
}
return ans;
}
private void dfs(int i) {
suspicious[i] = true;
for (int j : g[i]) {
if (!suspicious[j]) {
dfs(j);
}
}
}
private void dfs2(int i) {
vis[i] = true;
for (int j : f[i]) {
if (!vis[j]) {
suspicious[j] = false;
dfs2(j);
}
}
}
}class Solution {
public:
vector<int> remainingMethods(int n, int k, vector<vector<int>>& invocations) {
vector<bool> suspicious(n);
vector<bool> vis(n);
vector<int> f[n];
vector<int> g[n];
for (const auto& e : invocations) {
int a = e[0], b = e[1];
f[a].push_back(b);
f[b].push_back(a);
g[a].push_back(b);
}
auto dfs = [&](auto&& dfs, int i) -> void {
suspicious[i] = true;
for (int j : g[i]) {
if (!suspicious[j]) {
dfs(dfs, j);
}
}
};
dfs(dfs, k);
auto dfs2 = [&](auto&& dfs2, int i) -> void {
vis[i] = true;
for (int j : f[i]) {
if (!vis[j]) {
suspicious[j] = false;
dfs2(dfs2, j);
}
}
};
for (int i = 0; i < n; ++i) {
if (!suspicious[i] && !vis[i]) {
dfs2(dfs2, i);
}
}
vector<int> ans;
for (int i = 0; i < n; ++i) {
if (!suspicious[i]) {
ans.push_back(i);
}
}
return ans;
}
};func remainingMethods(n int, k int, invocations [][]int) []int {
suspicious := make([]bool, n)
vis := make([]bool, n)
f := make([][]int, n)
g := make([][]int, n)
for _, e := range invocations {
a, b := e[0], e[1]
f[a] = append(f[a], b)
f[b] = append(f[b], a)
g[a] = append(g[a], b)
}
var dfs func(int)
dfs = func(i int) {
suspicious[i] = true
for _, j := range g[i] {
if !suspicious[j] {
dfs(j)
}
}
}
dfs(k)
var dfs2 func(int)
dfs2 = func(i int) {
vis[i] = true
for _, j := range f[i] {
if !vis[j] {
suspicious[j] = false
dfs2(j)
}
}
}
for i := 0; i < n; i++ {
if !suspicious[i] && !vis[i] {
dfs2(i)
}
}
var ans []int
for i := 0; i < n; i++ {
if !suspicious[i] {
ans = append(ans, i)
}
}
return ans
}function remainingMethods(n: number, k: number, invocations: number[][]): number[] {
const suspicious: boolean[] = Array(n).fill(false);
const vis: boolean[] = Array(n).fill(false);
const f: number[][] = Array.from({ length: n }, () => []);
const g: number[][] = Array.from({ length: n }, () => []);
for (const [a, b] of invocations) {
f[a].push(b);
f[b].push(a);
g[a].push(b);
}
const dfs = (i: number) => {
suspicious[i] = true;
for (const j of g[i]) {
if (!suspicious[j]) {
dfs(j);
}
}
};
dfs(k);
const dfs2 = (i: number) => {
vis[i] = true;
for (const j of f[i]) {
if (!vis[j]) {
suspicious[j] = false;
dfs2(j);
}
}
};
for (let i = 0; i < n; i++) {
if (!suspicious[i] && !vis[i]) {
dfs2(i);
}
}
return Array.from({ length: n }, (_, i) => i).filter(i => !suspicious[i]);
}