| comments | difficulty | edit_url | tags | ||||
|---|---|---|---|---|---|---|---|
true |
Medium |
|
You are given the root of a binary tree and an integer k.
Return an integer denoting the size of the kth largest perfect binary subtree, or -1 if it doesn't exist.
A perfect binary tree is a tree where all leaves are on the same level, and every parent has two children.
Example 1:
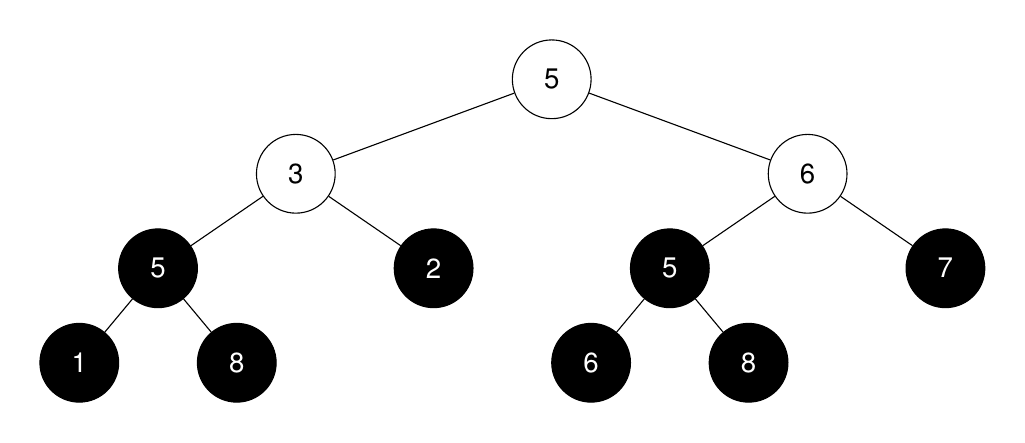
Input: root = [5,3,6,5,2,5,7,1,8,null,null,6,8], k = 2
Output: 3
Explanation:
The roots of the perfect binary subtrees are highlighted in black. Their sizes, in non-increasing order are [3, 3, 1, 1, 1, 1, 1, 1].
The 2nd largest size is 3.
Example 2:
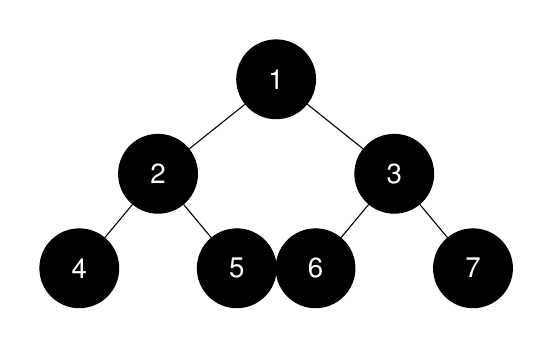
Input: root = [1,2,3,4,5,6,7], k = 1
Output: 7
Explanation:
The sizes of the perfect binary subtrees in non-increasing order are [7, 3, 3, 1, 1, 1, 1]. The size of the largest perfect binary subtree is 7.
Example 3:
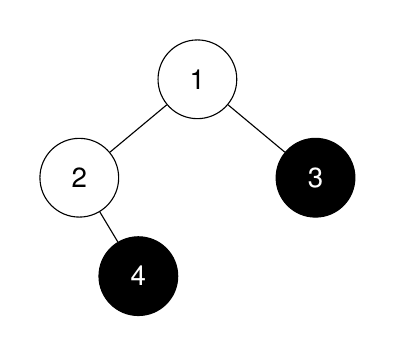
Input: root = [1,2,3,null,4], k = 3
Output: -1
Explanation:
The sizes of the perfect binary subtrees in non-increasing order are [1, 1]. There are fewer than 3 perfect binary subtrees.
Constraints:
- The number of nodes in the tree is in the range
[1, 2000]. 1 <= Node.val <= 20001 <= k <= 1024
We define a function
The execution process of the function
- If the current node is null, return
$0$ ; - Recursively calculate the sizes of the perfect binary subtrees of the left and right subtrees, denoted as
$l$ and$r$ respectively; - If the sizes of the left and right subtrees are not equal, or if the sizes of the left and right subtrees are less than
$0$ , return$-1$ ; - Calculate the size of the perfect binary subtree rooted at the current node
$\textit{cnt} = l + r + 1$ , and add$\textit{cnt}$ to the array$\textit{nums}$ ; - Return
$\textit{cnt}$ .
We call the
The time complexity is
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def kthLargestPerfectSubtree(self, root: Optional[TreeNode], k: int) -> int:
def dfs(root: Optional[TreeNode]) -> int:
if root is None:
return 0
l, r = dfs(root.left), dfs(root.right)
if l < 0 or l != r:
return -1
cnt = l + r + 1
nums.append(cnt)
return cnt
nums = []
dfs(root)
if len(nums) < k:
return -1
nums.sort(reverse=True)
return nums[k - 1]/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private List<Integer> nums = new ArrayList<>();
public int kthLargestPerfectSubtree(TreeNode root, int k) {
dfs(root);
if (nums.size() < k) {
return -1;
}
nums.sort(Comparator.reverseOrder());
return nums.get(k - 1);
}
private int dfs(TreeNode root) {
if (root == null) {
return 0;
}
int l = dfs(root.left);
int r = dfs(root.right);
if (l < 0 || l != r) {
return -1;
}
int cnt = l + r + 1;
nums.add(cnt);
return cnt;
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int kthLargestPerfectSubtree(TreeNode* root, int k) {
vector<int> nums;
auto dfs = [&](auto&& dfs, TreeNode* root) -> int {
if (!root) {
return 0;
}
int l = dfs(dfs, root->left);
int r = dfs(dfs, root->right);
if (l < 0 || l != r) {
return -1;
}
int cnt = l + r + 1;
nums.push_back(cnt);
return cnt;
};
dfs(dfs, root);
if (nums.size() < k) {
return -1;
}
ranges::sort(nums, greater<int>());
return nums[k - 1];
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func kthLargestPerfectSubtree(root *TreeNode, k int) int {
nums := []int{}
var dfs func(*TreeNode) int
dfs = func(root *TreeNode) int {
if root == nil {
return 0
}
l, r := dfs(root.Left), dfs(root.Right)
if l < 0 || l != r {
return -1
}
cnt := l + r + 1
nums = append(nums, cnt)
return cnt
}
dfs(root)
if len(nums) < k {
return -1
}
sort.Sort(sort.Reverse(sort.IntSlice(nums)))
return nums[k-1]
}/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function kthLargestPerfectSubtree(root: TreeNode | null, k: number): number {
const nums: number[] = [];
const dfs = (root: TreeNode | null): number => {
if (!root) {
return 0;
}
const l = dfs(root.left);
const r = dfs(root.right);
if (l < 0 || l !== r) {
return -1;
}
const cnt = l + r + 1;
nums.push(cnt);
return cnt;
};
dfs(root);
if (nums.length < k) {
return -1;
}
return nums.sort((a, b) => b - a)[k - 1];
}