We will find a solution by first considering 1D and 2D
We can assume that a point is first chosen such that
Thus
Let's assume
If
Through experimentation, we can see that
Thus
For a more analytical approach as we would have to do in higher dimensions, we can rearrange
From this equation we can see that when
And that when
Finally when
Thus we have the same equations that we found above.
This is an alternative method to the one posted on the Jane Street website from February 2020.
We can restrict our search to
Instead of calculating both
There are three cases we need to consider when finding
- Case 1: Arc intersects with
$x = 1$ only
$\theta_{top}$ represents the angle from the top of the circle to the point at which the circle intersects$x = 1$ . We can represent this by:
$x + d \cos(\frac{\pi}{2} - \theta_{top}) = 1$ ,$1 \leq y + d \sin(\frac{\pi}{2} - \theta_{top}) \leq 2$
These two equations mean that the circle will intersect$x = 1$ somewhere between$1 \leq y \leq 2$
We also have that$y + d \leq 2$ since the arc only intersects with$x = 1$ as defined in our case, not$y = 2$
Rearranging$x + d \cos(\frac{\pi}{2} - \theta_{top}) = 1$ gets us that$\theta_{top} = \sin^{-1}(\frac{1 - x}{d})$
Note that this angle is only valid when$1 - x \leq d$ , or rather$x + d \geq 1$ . This makes sense as in order for the circle to ever touch$x = 1$ this condition must be met. Thus$x \geq 1 - d$ , and we have that$\max(0, 1 - d) \leq x \leq 1$
The$y$ constraint gets us that$1 - d \sin(\frac{\pi}{2} - \theta_{top}) \leq y \leq 2 - d \sin(\frac{\pi}{2} - \theta_{top})$ , but since$y \leq 2 - d \leq 2 - d \sin(\frac{\pi}{2} - \theta_{top})$ , we really have that$1 - d \sin(\frac{\pi}{2} - \theta_{top}) \leq y \leq 2 - d$ . Thus$\max(0, 1 - d \sin(\cos^{-1}(\frac{1 - x}{d}))) \leq y \leq \min(1, 2 - d)$
For this bound, we need to make sure that when$d \geq 1$ that$\max(0, 1 - d \sin(\cos^{-1}(\frac{1 - x}{d}))) \leq 2 - d$ . It can be shown that$1 - d \sin(\cos^{-1}(\frac{1 - x}{d})) \leq 2 - d$ is always the case when$d \geq 1$ . And$0 \leq 2 - d$ when$d \leq 2$ . Thus we restrict case 1 to$0 \leq d \leq 2$ .
In summary:
$\theta_{top} = \sin^{-1}(\frac{1 - x}{d})$
$\max(0, 1 - d) \leq x \leq 1$
$\max(0, 1 - d \sin(\cos^{-1}(\frac{1 - x}{d}))) \leq y \leq \min(1, 2 - d)$
$0 \leq d \leq 2$
$P_1(d) = \frac{4}{\pi} \int_{\max(0, 1 - d)}^1 \int_{\max(0, 1 - d \sin(\cos^{-1}(\frac{1 - x}{d})))}^{\min(1, 2 - d)} \sin^{-1}(\frac{1 - x}{d}) dy dx$ for$0 \leq d \leq 2$
Note: I was surprised that Python was able to compute this integral even though the lower$y$ integral bound used the max function on a function that depended on$x$ . If it wasn't able to, then this integral could be separated into two integrals with different$x$ bounds to avoid this. - Case 2: Arc intersects with
$x = 1$ and$y = 2$
$\theta_{top}$ represents the angle from the point at which the circle intersects$y = 2$ ($\theta_1$ ) to the point at which the circle intersects$x = 1$ ($\theta_2$ ). We have already calculated$\theta_2$ above. Note that if the circle intersects with$y = 2$ it must intersect with$x = 1$ . It will not intersect with$y = 1$ or anything else. Thus if we only use the bounds for intersecting$y = 2$ this will also include the bounds for intersecting$x = 1$ . We don't need to also reuse the bounds from case 1. We can represent this by:
$y + d \sin(\frac{\pi}{2} - \theta_1) = 2$ ,$0 \leq x + d \cos(\frac{\pi}{2} - \theta_1) \leq 1$
These two equations mean that the circle will intersect$y = 2$ somewhere between$0 \leq x \leq 1$
We also have that$y + d \geq 2$ since the arc intersects with$y = 2$ as defined in our case
Rearranging$y + d \sin(\frac{\pi}{2} - \theta_1) = 2$ gets us that$\theta_1 = \cos^{-1}(\frac{2 - y}{d})$
Note that this angle is only valid when$2 - y \leq d$ , or rather$y + d \geq 2$ as expected. Thus$y \geq 2 - d$ , and we have that$\max(0, 2 - d) \leq y \leq 1$
The$x$ constraint gets us that$0 \leq x \leq 1 - d \cos(\frac{\pi}{2} - \theta_1)$ , and since$\theta_1 = \cos^{-1}(\frac{2 - y}{d}) = \frac{\pi}{2} - \sin^{-1}(\frac{2 - y}{d})$ , we have that$0 \leq x \leq 1 - d \cos(\sin^{-1}(\frac{2 - y}{d}))$
We also need to make sure that$0 \leq 1 - d \cos(\sin^{-1}(\frac{2 - y}{d}))$ . This happens when$y < 2 - d \sin(\cos^{-1}(\frac{1}{d}))$ . Thus our updated$y$ bound is$\max(0, 2 - d) \leq y \leq \min(1, 2 - d \sin(\cos^{-1}(\frac{1}{d})))$ .
Now we check the bounds for$d$ . We need$2 - d \leq 1$ from our$y$ bound. This occurs when$d \geq 1$ . We also need$0 \leq 2 - d \sin(\cos^{-1}(\frac{1}{d}))$ . This is true when$d \leq \sqrt{5}$ . Thus we restrict case 2 to$1 \leq d \leq \sqrt{5}$ .
In summary:
$\theta_{top} = \theta_2 - \theta_1 = \sin^{-1}(\frac{1 - x}{d}) - \cos^{-1}(\frac{2 - y}{d})$
$\max(0, 2 - d) \leq y \leq \min(1, 2 - d \sin(\cos^{-1}(\frac{1}{d})))$
$0 \leq x \leq 1 - d \cos(\sin^{-1}(\frac{2 - y}{d}))$
$1 \leq d \leq \sqrt{5}$
$P_2(d) = \frac{4}{\pi} \int_{\max(0, 2 - d)}^{\min(1, 2 - d \sin(\cos^{-1}(\frac{1}{d})))} \int_0^{1 - d \cos(\sin^{-1}(\frac{2 - y}{d}))} \left[\sin^{-1}(\frac{1 - x}{d}) - \cos^{-1}(\frac{2 - y}{d}) \right] dx dy$ for$1 \leq d \leq \sqrt{5}$ - Case 3: Arc intersects with
$y = 1$
$\theta_{top}$ represents the angle from the top of the circle to the point at which the circle intersects$y = 1$ . We can represent this by:
$y + d \sin(\frac{\pi}{2} - \theta_{top}) = 1$ ,$0 \leq x + d \cos(\frac{\pi}{2} - \theta_{top}) \leq 1$
These two equations mean that the circle will intersect$y = 1$ somewhere between$0 \leq x \leq 1$
We also have that$y + d \geq 1$ since the arc intersects with$y = 1$ as defined in our case
Rearranging$y + d \sin(\frac{\pi}{2} - \theta_{top}) = 1$ gets us that$\theta_{top} = \cos^{-1}(\frac{1 - y}{d})$
Note that this angle is only valid when$1 - y \leq d$ , or rather$y + d \geq 1$ as expected. Thus$y \geq 1 - d$ , and we have that$\max(0, 1 - d) \leq y \leq 1$
The$x$ constraint again gets us that$0 \leq x \leq 1 - d \cos(\frac{\pi}{2} - \theta_{top})$ , and since$\theta_{top} = \cos^{-1}(\frac{1 - y}{d}) = \frac{\pi}{2} - \sin^{-1}(\frac{1 - y}{d})$ , we have that$0 \leq x \leq 1 - d \cos(\sin^{-1}(\frac{1 - y}{d}))$
Again, we also need to make sure that$0 \leq 1 - d \cos(\sin^{-1}(\frac{1 - y}{d}))$ . This happens when$y < 1 - d \sin(\cos^{-1}(\frac{1}{d}))$ . Thus our updated$y$ bound is$\max(0, 1 - d) \leq y \leq \min(1, 1 - d \sin(\cos^{-1}(\frac{1}{d})))$ .
Note:$\cos^{-1}(\frac{1}{d})$ is undefined when$d < 1$ , so in this case$y = 1$ will be the upper bound. This is different from case 2, where$d < 1$ did not need to be considered.
Again we check the bounds for$d$ . We need$1 - d \leq 1$ , which is always true for a non-negative$d$ . We also need$0 \leq 1 - d \sin(\cos^{-1}(\frac{1}{d}))$ . This is true when$d \leq \sqrt{2}$ . Thus we restrict case 3 to$0 \leq d \leq \sqrt{2}$ .
In summary:
$\theta_{top} = \cos^{-1}(\frac{1 - y}{d})$
$\max(0, 1 - d) \leq y \leq \min(1, 1 - d \sin(\cos^{-1}(\frac{1}{d})))$ (with$y \leq 1$ when$d < 1$ )
$0 \leq x \leq 1 - d \cos(\sin^{-1}(\frac{1 - y}{d}))$
$1 \leq d \leq \sqrt{5}$
$P_3(d) = \frac{4}{\pi} \int_{\max(0, 1 - d)}^{\min(1, 1 - d \sin(\cos^{-1}(\frac{1}{d})))} \int_0^{1 - d \cos(\sin^{-1}(\frac{1 - y}{d}))} \cos^{-1}(\frac{1 - y}{d}) dx dy$ for$0 \leq d \leq \sqrt{2}$
Finally, we get that
Instead of computing the integrals and finding the derivatives, we can graphically find the value of
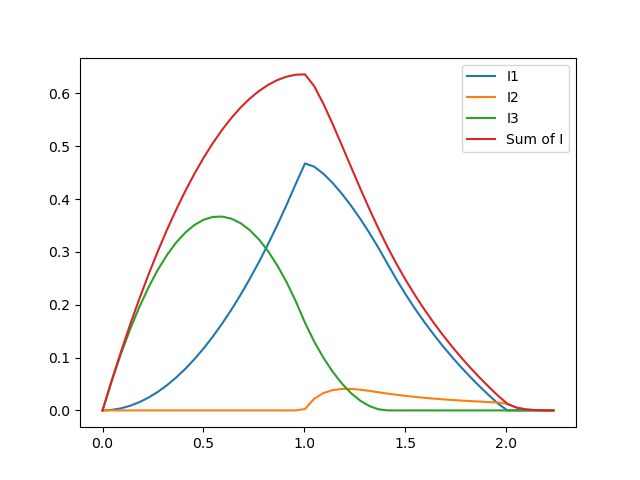
We can see that in 2-space
Here is a graph of the
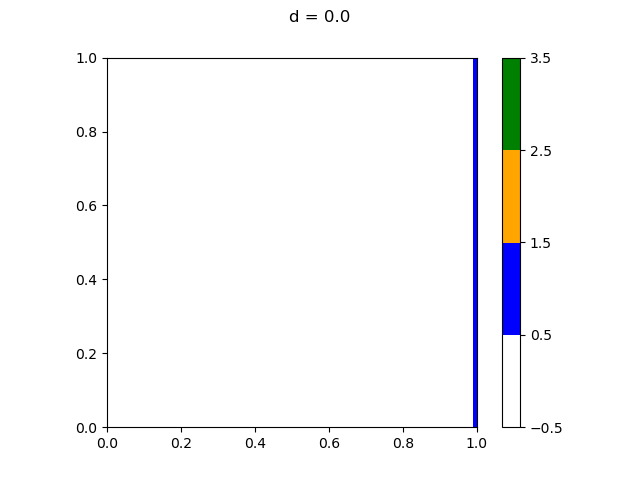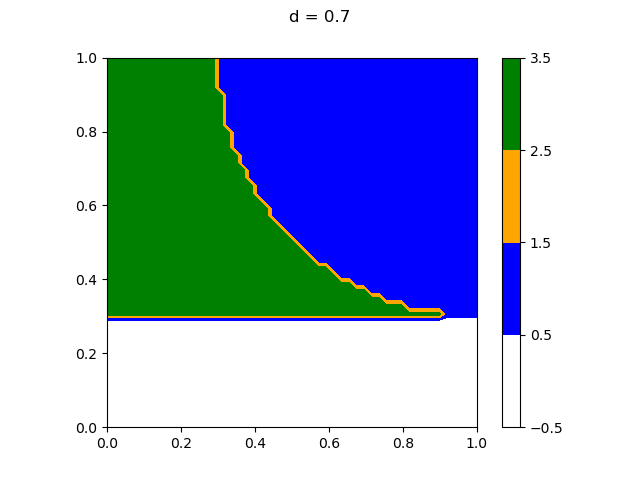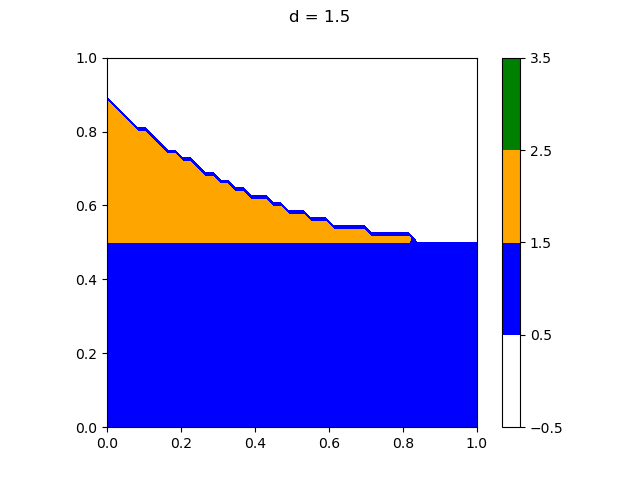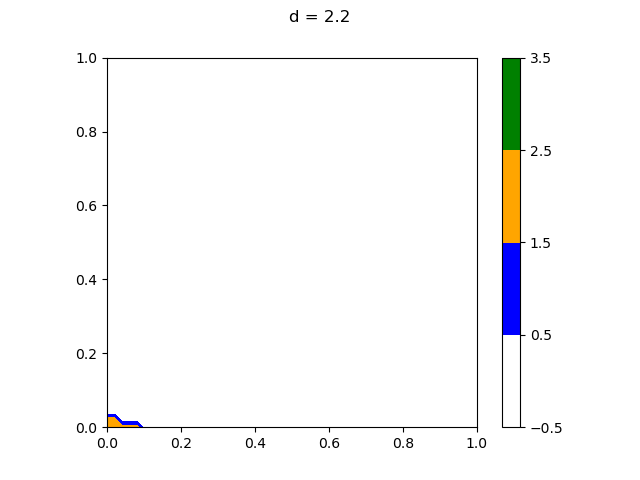
This is an alternative solution that is a much more complex method than the official solution. Unfortunately I just really wanted to extend my 2D solution to 3D.
We can restrict our search to
Similar to how we only considered
Actually we will restrict our search to
From this point there are two ways to go about this. The first method involves adding up the cases where the octant doesn't intersect with either the
The second method involves adding up the eighth spherical caps that intersect with
The surface area of a spherical cap is
- Case 1: The base of the spherical cap included in the probability touches
$z = 1$ . To be included in the probability means that a portion of the circle at$z = 1$ is within the box found by$0 \leq x \leq 1$ ,$0 \leq y \leq 1$ . So we require that$z + d \geq 1$ since our spherical cap touches$z = 1$ . Thus$1 - d \leq z \leq 1$ . The way we determine that our spherical cap touches$z = 1$ is if the radius of the circle at$z = 1$ is less than or equal to the distance from$(x, y)$ to$(1, 1)$ . If the circle goes past$(1, 1)$ , then none of the circle will be within the box found by$0 \leq x \leq 1$ ,$0 \leq y \leq 1$ . The base of the spherical cap included in the probability will be above$z = 1$ .
Note that the height of our circle relative to the center of the sphere$(x, y, z)$ at$z = 1$ is$1 - z$ ($z = 1$ is just referring to the axis, this is not our$z$ value in$1 - z$ ). In spherical coordinates,$height = 1 - z = d \cos(\phi)$ , thus$\phi = \cos^{-1}(\frac{1 - z}{d})$ . Our radius at$z = 1$ is$d \sin(\phi) = d \sin(\cos^{-1}(\frac{1 - z}{d}))$ .
So we want$d \sin(\cos^{-1}(\frac{1 - z}{d})) \leq \sqrt{(x - 1)^2 + (y - 1)^2}$
Rearranging this gives us that$x \leq 1 - \sqrt{(d \sin(\cos^{-1}(\frac{1 - z}{d})))^2 - (y - 1)^2}$
We want$(d \sin(\cos^{-1}(\frac{1 - z}{d})))^2 - (y - 1)^2 \geq 0$ so the square root term remains real. This occurs when$y \geq 1 - d \sin(\cos^{-1}(\frac{1 - z}{d}))$ . This case will be broken down into two subcases, when$y$ is less than this value, and when$y$ is greater than this value.- Subcase 1:
$0 \leq y \leq 1 - d \sin(\cos^{-1}(\frac{1 - z}{d}))$
This occurs when$y + r \leq 1$ , where$r$ is the radius of the circle at$z = 1$
Because$y + r \leq 1$ at$z = 1$ , there will always be a part of the circle that is contained within the box$0 \leq x, y \leq 1$ regardless of the$x$ value. So our$x$ bound is$0 \leq x \leq 1$
For our surface area$\frac{1}{2} \pi r h$ , we have$r = d$ and$h = z + d - 1$ (since the top of the spherical cap will always be included, and our cap touches$z = 1$ ).
In summary:
Surface area =$\frac{1}{2} \pi d (z + d - 1)$
$1 - d \leq z \leq 1$
$0 \leq y \leq 1 - d \sin(\cos^{-1}(\frac{1 - z}{d}))$
$0 \leq x \leq 1$
$P_1(d) = \frac{6}{\pi d^2} \int_{1 - d}^1 \int_0^{1 - d \sin(\cos^{-1}(\frac{1 - z}{d}))} \int_0^1 \left[ \frac{1}{2} \pi d \left( z + d - 1 \right) \right] dx dy dz$ - Subcase 2:
Surface area and$z$ bounds same as subcase 1
$1 - d \sin(\cos^{-1}(\frac{1 - z}{d})) \leq y \leq 1$
$0 \leq x \leq 1 - \sqrt{(d \sin(\cos^{-1}(\frac{1 - z}{d})))^2 - (y - 1)^2}$
$P_{1.2}(d) = \frac{6}{\pi d^2} \int_{1 - d}^1 \int_{1 - d \sin(\cos^{-1}(\frac{1 - z}{d}))}^1 \int_0^{1 - \sqrt{(d \sin(\cos^{-1}(\frac{1 - z}{d})))^2 - (y - 1)^2}} \left[ \frac{1}{2} \pi d \left( z + d - 1 \right) \right] dx dy dz$
- Subcase 1:
- Case 2: The base of the spherical cap included in the probability will be at
$1 < z \leq 2$ .
We have the same bounds as case 1 subcase 2, except now that$1 - \sqrt{(d \sin(\cos^{-1}(\frac{1 - z}{d})))^2 - (y - 1)^2} \leq x \leq 1$ since we want the radius of the circle at$z = 1$ to be greater than the distance from$(x, y)$ to$(1, 1)$ .
The base of the spherical cap occurs when$r = \sqrt{(x - 1)^2 + (y - 1)^2}$
Since$r = d \sin(\phi)$ , we have that$\phi = \sin^{-1}(\frac{r}{d}) = \sin^{-1}(\frac{1}{d} \sqrt{(x - 1)^2 + (y - 1)^2})$
The height of this circle relative to the center of the sphere in this case is$d \cos(\phi) = d \cos(\sin^{-1}(\frac{1}{d} \sqrt{(x - 1)^2 + (y - 1)^2}))$
Thus the height of the spherical cap that we are interested in for our surface area is$d - d \cos(\sin^{-1}(\frac{1}{d} \sqrt{(x - 1)^2 + (y - 1)^2}))$
In summary:
Surface area =$\frac{1}{2} \pi d (d - d \cos(\sin^{-1}(\frac{1}{d} \sqrt{(x - 1)^2 + (y - 1)^2})))$
$1 - d \leq z \leq 1$
$1 - d \sin(\cos^{-1}(\frac{1 - z}{d})) \leq y \leq 1$
$1 - \sqrt{(d \sin(\cos^{-1}(\frac{1 - z}{d})))^2 - (y - 1)^2} \leq x \leq 1$
$P_2(d) = \frac{6}{\pi d^2} \int_{1 - d}^1 \int_{1 - d \sin(\cos^{-1}(\frac{1 - z}{d}))}^1 \int_{1 - \sqrt{(d \sin(\cos^{-1}(\frac{1 - z}{d})))^2 - (y - 1)^2}}^1 \left[ \frac{1}{2} \pi d \left( d - d \cos(\sin^{-1}(\frac{1}{d} \sqrt{(x - 1)^2 + (y - 1)^2})) \right) \right] dx dy dz$
For the next two cases we need to subtract off the parts of the quarter spherical caps we found in the first two cases that are not included in the cube found by
Since
- Case 3:
Let$r = d \sin(\phi)$ represent the radius of the circle found at some$\phi$ value. For our surface area$SA(x, y, z, d)$ , we want$\theta \geq 0$ and$x + r \cos(\theta) \geq 1$ , which gives us$\theta \leq \cos^{-1}(\frac{1 - x}{r}) = \cos^{-1}(\frac{1 - x}{d \sin(\phi)})$ . Thus$0 \leq \theta \leq \cos^{-1}(\frac{1 - x}{d \sin(\phi)})$
For$\cos^{-1}(\frac{1 - x}{d \sin(\phi)})$ to be defined we also need$1 - x \leq d \sin(\phi)$ . This is just saying that$x + r \geq 1$ . This gives us that$\phi \geq \sin^{-1}(\frac{1 - x}{d})$ . Also this requires that$1 - x \leq d$ , but if$x + r \geq 1$ then it must be the case that$x + d \geq 1$ so we don't need to add any bounds for this. We also want$z + d \cos(\phi) \geq 1$ , which gives us that$\phi \leq \cos^{-1}(\frac{1 - z}{d})$ . Thus$\sin^{-1}(\frac{1 - x}{d}) \leq \phi \leq \cos^{-1}(\frac{1 - z}{d})$
So$SA(x, y, z, d) = d^2 \int_{\sin^{-1}(\frac{1 - x}{d})}^{\cos^{-1}(\frac{1 - z}{d})} \cos^{-1}(\frac{1 - x}{d \sin(\phi)}) \sin(\phi) d \phi$
$P_3(d) = -2 \cdot \frac{6}{\pi d^2} \int \int \int SA(x, y, z, d) dV$
$= -\frac{12}{\pi} \int \int \int \int_{\sin^{-1}(\frac{1 - x}{d})}^{\cos^{-1}(\frac{1 - z}{d})} \cos^{-1}(\frac{1 - x}{d \sin(\phi)}) \sin(\phi) d \phi dV$ - Subcase 1: This mirrors subcase 1 from above with a stricter
$x$ bound
$1 - d \leq z \leq 1$
$0 \leq y \leq 1 - d \sin(\cos^{-1}(\frac{1 - z}{d}))$
$1 - d \sin(\cos^{-1}(\frac{1 - z}{d})) \leq x \leq 1$
$P_3(d) = -\frac{12}{\pi} \int_{1 - d}^1 \int_0^{1 - d \sin(\cos^{-1}(\frac{1 - z}{d}))} \int_{1 - d \sin(\cos^{-1}(\frac{1 - z}{d}))}^1 \int_{\sin^{-1}(\frac{1 - x}{d})}^{\cos^{-1}(\frac{1 - z}{d})} \cos^{-1}(\frac{1 - x}{d \sin(\phi)}) \sin(\phi) d \phi dx dy dz$ - Subcase 2: This mirrors subcase 2 from above with a stricter
$x$ bound
$1 - d \leq z \leq 1$
$1 - d \sin(\cos^{-1}(\frac{1 - z}{d})) \leq y \leq 1$
$1 - d \sin(\cos^{-1}(\frac{1 - z}{d})) \leq x \leq 1 - \sqrt{(d \sin(\cos^{-1}(\frac{1 - z}{d})))^2 - (y - 1)^2}$
$P_{3.2}(d) = -\frac{12}{\pi} \int_{1 - d}^1 \int_{1 - d \sin(\cos^{-1}(\frac{1 - z}{d}))}^1 \int_{1 - d \sin(\cos^{-1}(\frac{1 - z}{d}))}^{1 - \sqrt{(d \sin(\cos^{-1}(\frac{1 - z}{d})))^2 - (y - 1)^2}} \int_{\sin^{-1}(\frac{1 - x}{d})}^{\cos^{-1}(\frac{1 - z}{d})} \cos^{-1}(\frac{1 - x}{d \sin(\phi)}) \sin(\phi) d \phi dx dy dz$
- Subcase 1: This mirrors subcase 1 from above with a stricter
- Case 4: This case mirrors case 2.
Recall from case 2 that the base of the spherical cap occurs at$\phi = \sin^{-1}(\frac{1}{d} \sqrt{(x - 1)^2 + (y - 1)^2})$
This will act as our upper bound for$\phi$ in our equation for surface area. Thus our new$\phi$ bound is$\sin^{-1}(\frac{1 - x}{d}) \leq \phi \leq \sin^{-1}(\frac{1}{d} \sqrt{(x - 1)^2 + (y - 1)^2})$
Note it can be shown that this lower bound is strictly less than this upper bound (for non-negative values at least). The remainder of the surface area equation from case 3 remains unchanged.
Thus$SA(x, y, z, d) = d^2 \int_{\sin^{-1}(\frac{1 - x}{d})}^{\sin^{-1}(\frac{1}{d} \sqrt{(x - 1)^2 + (y - 1)^2})} \cos^{-1}(\frac{1 - x}{d \sin(\phi)}) \sin(\phi) d \phi$
The$x$ ,$y$ ,$z$ bounds will exactly the same as case 2, since case 2's lower$x$ bound is already stricter than (greater than or equal to) the new lower$x$ bound we found for these last two cases.
Meaning that$1 - \sqrt{(d \sin(\cos^{-1}(\frac{1 - z}{d})))^2 - (y - 1)^2} \geq 1 - d \sin(\cos^{-1}(\frac{1 - z}{d}))$
Thus
$1 - d \leq z \leq 1$
$1 - d \sin(\cos^{-1}(\frac{1 - z}{d})) \leq y \leq 1$
$1 - \sqrt{(d \sin(\cos^{-1}(\frac{1 - z}{d})))^2 - (y - 1)^2} \leq x \leq 1$
$P_4(d) = -\frac{12}{\pi} \int_{1 - d}^1 \int_{1 - d \sin(\cos^{-1}(\frac{1 - z}{d}))}^1 \int_{1 - \sqrt{(d \sin(\cos^{-1}(\frac{1 - z}{d})))^2 - (y - 1)^2}}^1 \int_{\sin^{-1}(\frac{1 - x}{d})}^{\sin^{-1}(\frac{1}{d} \sqrt{(x - 1)^2 + (y - 1)^2})} \cos^{-1}(\frac{1 - x}{d \sin(\phi)}) \sin(\phi) d \phi dx dy dz$
FINALLY,
Unfortunately, when I tried to have Python calculate this for
Q. E. D.