- 그라데이션 원리, pow, sqrt, step, smoothstep
- 선 그리기
- Sine과 Cosine의 규칙성
- 그래픽을 위한 수학 자료
The Book of Shaders에 소개된 예제를 통해 GLSL에 더 익숙해져 보겠습니다.
위 예제에서 그라데이션을 그리는 부분만 남겼고요, 각 코드 라인에 주석으로 해설을 남겼습니다. GLSL은 각 GPU 쓰레드에 동일하게 전달되고 동시에 처리된다는 것을 상기하면서 보시면 좋을 것 같습니다. 물론 gl_FragCoord 변수는 각 쓰레드의 정보를 담고 있으므로 서로 다른 데이터를 갖고 있겠지요.
#ifdef GL_ES
// 중간 정도의 precision을 사용하겠다고 명령
precision mediump float;
#endif
// Canvas 사이즈
uniform vec2 u_resolution;
void main() {
// st = 0.0 - 1.0 사의의 값으로 변환된 각 픽셀의 x, y 좌표값
// 각 픽셀의 좌표값을 사용해서 픽셀마다 다른 색상을 입혀줄 것이기 때문에 0.0 - 1.0 사이의 값으로 변환
// 색상 vec3/vec4 에서 R, G, B의 밝기를 나타내는 0.0 - 1.0 사이의 값을 사용하며 하나의 색을 만들기 때문
vec2 st = gl_FragCoord.xy / u_resolution;
// 각 픽셀의 x 좌표값에만 비례하는 색상값 추출
float colorValue = st.x;
// vec3(y) => vec3(y, y, y)
// RGB 값의 밝기 값이 동일하면 무채색이 나옵니다
vec3 color = vec3(colorValue);
// vec4(color, 1.0) => vec4(color, color, color, 1.0)
gl_FragColor = vec4(color, 1.0);
}위 코드의 결과물은 다음과 같이 좌우로 Linear한 그라데이션이 됩니다.
픽셀의 x 좌표값을 다른 방식으로 가공해서 조금 다른 그라이데션도 만들어볼 수 있겠습니다. 가령 아래와 같이 pow나 sqrt 함수를 사용할 수 있겠지요. pow 와 같은 GLSL 내장함수는 코드를 해석하는 별도의 소프트웨어 엔진을 거치지 않고, GPU로 직접 전달되어 하드웨어에서 실행되기 때문에 실행 속도가 매우 빠릅니다. 화려한 인터렉션도 부드럽게 구현할 수 있는 이유이지요.
// x 좌표값의 1 제곱값인 색상 추출
float colorValue = pow(st.x, 1.0);
// x 좌표값의 2 제곱값인 색상 추출
float colorValue = pow(st.x, 2.0);
// x 좌표값의 3 제곱값인 색상 추출
float colorValue = pow(st.x, 3.0);
// x 좌표값의 제곱근인 색상 추출 => pow와 반대되는 그라데이션을 만들 수 있습니다
float colorValue = sqrt(st.x);step 역시 GLSL의 내장된 함수인데요, step(threshold, value)와 같이 2개의 파라미터를 사용하여 호출할 수 있습니다. 두번째 파라미터의 값이 첫번째 파라미터의 값(threshold)보다 크면 1.1, 작으면 0.0을 반환하는 함수입니다.
// 두번째 파라미터 값이 0.5 미만이면 0.0 반환
// st.x는 0.0 - 1.0 사이의 값으로 변환된 x 좌표값이므로
// 절반 미만인 좌측에 대해 0.0 반환
// 절반 이상인 우측에 대해 1.1 반환
float colorValue = step(0.5, st.x);smoothstep은 threshold 값을 범위로 지정하여 0.0과 1.0 사이의 값을 변환하도록 허용하는 함수입니다. smoothstep(threshold_start, threshold_end, value)와 같이 실행하면 됩니다.
// 0.4 - 0.6 사이의 값에 대해서는 0.0 혹은 1.0이 아닌 그 사이의 interpolation 값 반환
float colorValue = smoothstep(0.4, 0.6, st.x);위의 예제를 통해 GLSL의 vec2, vec3, vec4 타입과 gl_FragCoord 변수, step과 smoothstep와 같은 내장 함수를 조금 더 이해할 수 있게 되셨기를 바랍니다. 이제 선을 그리는 예제 코드를 살펴보면서 step과 smoothstep 함수를 더 활용해보겠습니다.
다음과 같이 x 좌표와 y 좌표 값이 동일한 지점을 잇는 선을 그려볼텐데요. 특정 조건을 만족하는 영역에만 녹색을 입히고, 나머지 부분에는 색을 지정하지 않는 이분법적인 접근을 하면 되므로, step이나 smoothstep 함수를 활용할 수 있겠습니다.
#ifdef GL_ES
precision mediump float;
#endif
uniform vec2 u_resolution;
// 파라미터 st 0.0 - 1.0 사이의 값으로 변환된 x,y 좌표값
float plot(vec2 st) {
// x, y 값이 일치하는 픽셀은 st.y - st.x 값이 0
float xyDiff = abs(st.y - st.x);
// x, y 값이 일치하는 픽셀을 이어 선을 그을 때
// step(0.0, xyDiff)를 사용하면 선의 두께가 없어 눈으로 볼 수 없으므로
// smoothstep을 사용해서 선의 두께를 만들어줌
return smoothstep(0.0, 0.02, xyDiff);
}
void main() {
vec2 st = gl_FragCoord.xy / u_resolution;
float colorValue = st.x;
vec3 color = vec3(colorValue);
// 선이 지나지 않는 좌표의 pct = 1.0
// 선이 지나는 좌표의 pct = 0.0 ~ 0.02
float pct = plot(st);
vec3 green = vec3(0.0, 1.0, 0.0);
// pct * color: 선이 지나지 않는 "pct = 1.0"인 경우, 본래 색상 할당
// (1.0 - pct) * green: 선이 지나는 곳은 녹색 값 할당
color = pct * color + (1.0 - pct) * green;
gl_FragColor = vec4(color, 1.0);
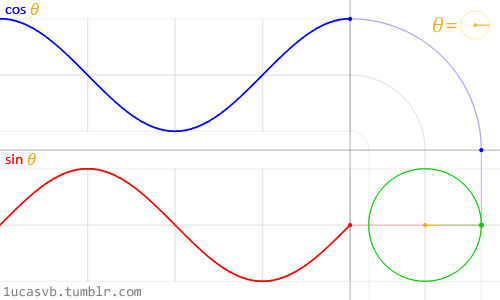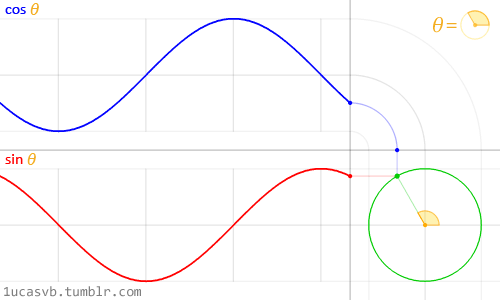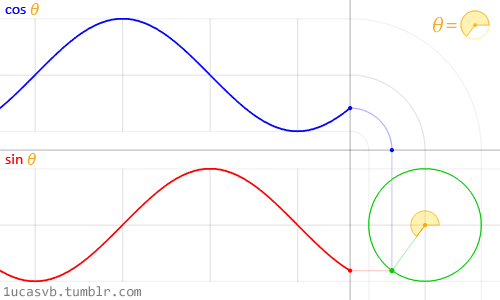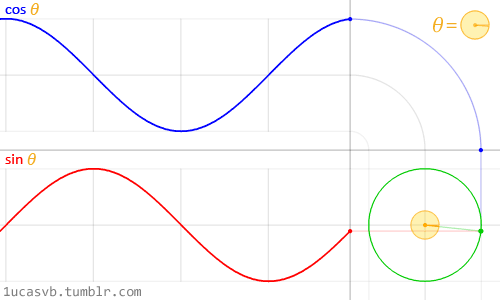
}컴퓨터 그래픽 분야에서는 Sine, Cosine과 같은 삼각함수 계산법이 매우 많이 사용되는데요, 이는 특정 조건 하에서 입력값에 따른 반환 값이 특정 범위내의 연속된 값들로 분포되는 삼각함수의 수학적 특징 때문입니다. 대표적으로, 반지름이 1인 원의 둘레를 이루는 점들의 (𝙭, 𝙮) 좌표를 Sine, Cosine 함수로 매우 쉽게 얻어낼 수 있는데요, 반지름이 1인 원의 둘레를 이루기 때문에 원의 중앙 좌표가 (0, 0)이라고 가정하면 그 값들은 -1에서 1 사이의 연속된 값들로 구성됩니다.
삼각함수가 잘 기억나지 않으시는 분들은 피타고라스 정리와 함께 다음 식을 참고해보셔도 좋겠습니다.
𝙘𝙤𝙨𝜭 = 𝙭 / √(𝙭𝟮 + 𝙮𝟮)
𝙨𝙞𝙣𝜭 = 𝙮 / √(𝙭𝟮 + 𝙮𝟮)
∴ (𝙭, 𝙮) = (𝙘𝙤𝙨𝜭, 𝙨𝙞𝙣𝜭), 𝙞𝙛 √(𝙭𝟮 + 𝙮𝟮) = 1
위의 Sine 그래프를 식으로 나타내면 다음과 같은 x, y의 관계식을 얻을 수 있습니다.
𝙮 = 𝙨𝙞𝙣(𝙭)
다음은 그래픽 구현에 활용할 만한 수학 자료들입니다.