There is a street with n * 2 plots, where there are n plots on each side of the street. The plots on each side are numbered from 1 to n. On each plot, a house can be placed.
Return the number of ways houses can be placed such that no two houses are adjacent to each other on the same side of the street. Since the answer may be very large, return it modulo 109 + 7.
Note that if a house is placed on the ith plot on one side of the street, a house can also be placed on the ith plot on the other side of the street.
Input: n = 1 Output: 4 Explanation: Possible arrangements: 1. All plots are empty. 2. A house is placed on one side of the street. 3. A house is placed on the other side of the street. 4. Two houses are placed, one on each side of the street.
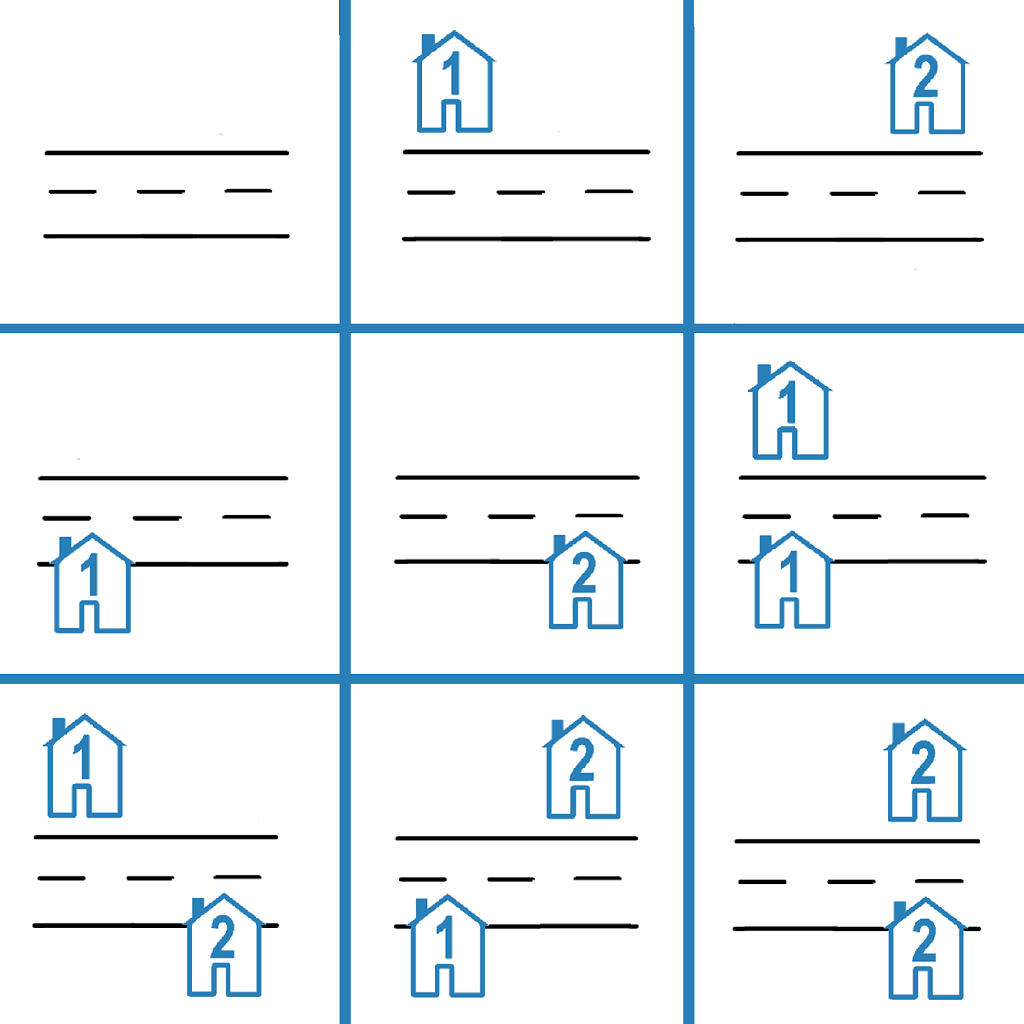
Input: n = 2 Output: 9 Explanation: The 9 possible arrangements are shown in the diagram above.
1 <= n <= 104
impl Solution {
pub fn count_house_placements(n: i32) -> i32 {
let n = n as usize;
let mut dp = vec![[0, 0]; n];
dp[0] = [1, 1];
for i in 1..n {
dp[i][0] = (dp[i - 1][0] + dp[i - 1][1]) % 1_000_000_007;
dp[i][1] = dp[i - 1][0];
}
(((dp[n - 1][0] + dp[n - 1][1]) as i64).pow(2) % 1_000_000_007) as i32
}
}