feat: add No.1014,1937

1001-1100/1014. Best Sightseeing Pair.md

@@ -0,0 +1,67 @@
+# 1014. Best Sightseeing Pair
+
+- Difficulty: Medium.
+- Related Topics: Array, Dynamic Programming.
+- Similar Questions: .
+
+## Problem
+
+You are given an integer array `values` where values[i] represents the value of the `ith` sightseeing spot. Two sightseeing spots `i` and `j` have a **distance** `j - i` between them.
+
+The score of a pair (`i < j`) of sightseeing spots is `values[i] + values[j] + i - j`: the sum of the values of the sightseeing spots, minus the distance between them.
+
+Return **the maximum score of a pair of sightseeing spots**.
+
+
+Example 1:
+
+```
+Input: values = [8,1,5,2,6]
+Output: 11
+Explanation: i = 0, j = 2, values[i] + values[j] + i - j = 8 + 5 + 0 - 2 = 11
+```
+
+Example 2:
+
+```
+Input: values = [1,2]
+Output: 2
+```
+
+
+**Constraints:**
+
+
+
+- `2 <= values.length <= 5 * 104`
+
+- `1 <= values[i] <= 1000`
+
+
+
+## Solution
+
+```javascript
+/**
+ * @param {number[]} values
+ * @return {number}
+ */
+var maxScoreSightseeingPair = function(values) {
+    var last = 0;
+    var max = Number.MIN_SAFE_INTEGER;
+    for (var i = 0; i < values.length; i++) {
+        max = Math.max(max, last + values[i] - i);
+        last = Math.max(last, values[i] + i);
+    }
+    return max;
+};
+```
+
+**Explain:**
+
+nope.
+
+**Complexity:**
+
+* Time complexity : O(n).
+* Space complexity : O(1).

1901-2000/1937. Maximum Number of Points with Cost.md

@@ -0,0 +1,116 @@
+# 1937. Maximum Number of Points with Cost
+
+- Difficulty: Medium.
+- Related Topics: Array, Dynamic Programming.
+- Similar Questions: Minimum Path Sum, Minimize the Difference Between Target and Chosen Elements.
+
+## Problem
+
+You are given an `m x n` integer matrix `points` (**0-indexed**). Starting with `0` points, you want to **maximize** the number of points you can get from the matrix.
+
+To gain points, you must pick one cell in **each row**. Picking the cell at coordinates `(r, c)` will **add** `points[r][c]` to your score.
+
+However, you will lose points if you pick a cell too far from the cell that you picked in the previous row. For every two adjacent rows `r` and `r + 1` (where `0 <= r < m - 1`), picking cells at coordinates `(r, c1)` and `(r + 1, c2)` will **subtract** `abs(c1 - c2)` from your score.
+
+Return **the **maximum** number of points you can achieve**.
+
+`abs(x)` is defined as:
+
+
+
+- `x` for `x >= 0`.
+
+- `-x` for `x < 0`.
+
+
+
+Example 1:** **
+
+![](https://assets.leetcode.com/uploads/2021/07/12/screenshot-2021-07-12-at-13-40-26-diagram-drawio-diagrams-net.png)
+
+```
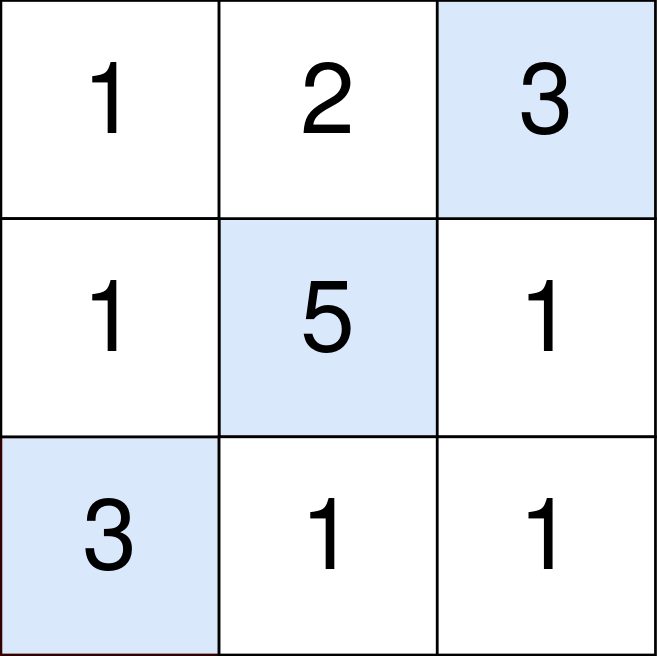
+Input: points = [[1,2,3],[1,5,1],[3,1,1]]
+Output: 9
+Explanation:
+The blue cells denote the optimal cells to pick, which have coordinates (0, 2), (1, 1), and (2, 0).
+You add 3 + 5 + 3 = 11 to your score.
+However, you must subtract abs(2 - 1) + abs(1 - 0) = 2 from your score.
+Your final score is 11 - 2 = 9.
+```
+
+Example 2:
+
+![](https://assets.leetcode.com/uploads/2021/07/12/screenshot-2021-07-12-at-13-42-14-diagram-drawio-diagrams-net.png)
+
+```
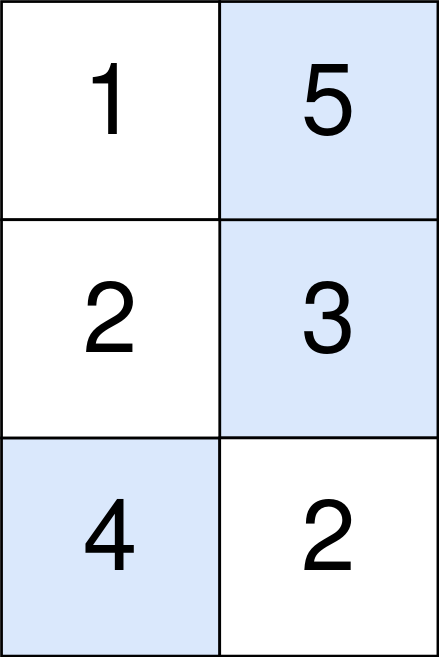
+Input: points = [[1,5],[2,3],[4,2]]
+Output: 11
+Explanation:
+The blue cells denote the optimal cells to pick, which have coordinates (0, 1), (1, 1), and (2, 0).
+You add 5 + 3 + 4 = 12 to your score.
+However, you must subtract abs(1 - 1) + abs(1 - 0) = 1 from your score.
+Your final score is 12 - 1 = 11.
+```
+
+
+**Constraints:**
+
+
+
+- `m == points.length`
+
+- `n == points[r].length`
+
+- `1 <= m, n <= 105`
+
+- `1 <= m * n <= 105`
+
+- `0 <= points[r][c] <= 105`
+
+
+
+## Solution
+
+```javascript
+/**
+ * @param {number[][]} points
+ * @return {number}
+ */
+var maxPoints = function(points) {
+    var m = points.length;
+    var n = points[0].length;
+    var maxArr = points[m - 1];
+    for (var i = m - 2; i >= 0; i--) {
+        var [prefixMaxArr, suffixMaxArr] = getMaxArr(maxArr);
+        for (var j = 0; j < n; j++) {
+            maxArr[j] = points[i][j] + Math.max(prefixMaxArr[j] - j, suffixMaxArr[j] + j);
+        }
+    }
+    return Math.max(...maxArr);
+};
+
+var getMaxArr = function(arr) {
+    var prefixMaxArr = Array(arr.length);
+    var max = Number.MIN_SAFE_INTEGER;
+    for (var i = 0; i < arr.length; i++) {
+        max = Math.max(max, arr[i] + i);
+        prefixMaxArr[i] = max;
+    }
+    var suffixMaxArr = Array(arr.length);
+    max = Number.MIN_SAFE_INTEGER;
+    for (var i = arr.length - 1; i >= 0; i--) {
+        max = Math.max(max, arr[i] - i);
+        suffixMaxArr[i] = max;
+    }
+    return [prefixMaxArr, suffixMaxArr];
+};
+```
+
+**Explain:**
+
+nope.
+
+**Complexity:**
+
+* Time complexity : O(m * n).
+* Space complexity : O(n).