feat: solve No.1334

1301-1400/1334. Find the City With the Smallest Number of Neighbors at a Threshold Distance.md

@@ -0,0 +1,123 @@
+# 1334. Find the City With the Smallest Number of Neighbors at a Threshold Distance
+
+- Difficulty: Medium.
+- Related Topics: Dynamic Programming, Graph, Shortest Path.
+- Similar Questions: Second Minimum Time to Reach Destination.
+
+## Problem
+
+There are `n` cities numbered from `0` to `n-1`. Given the array `edges` where `edges[i] = [fromi, toi, weighti]` represents a bidirectional and weighted edge between cities `fromi` and `toi`, and given the integer `distanceThreshold`.
+
+Return the city with the smallest number of cities that are reachable through some path and whose distance is **at most** `distanceThreshold`, If there are multiple such cities, return the city with the greatest number.
+
+Notice that the distance of a path connecting cities ****i**** and ****j**** is equal to the sum of the edges' weights along that path.
+
+
+Example 1:
+
+![](https://assets.leetcode.com/uploads/2020/01/16/find_the_city_01.png)
+
+```
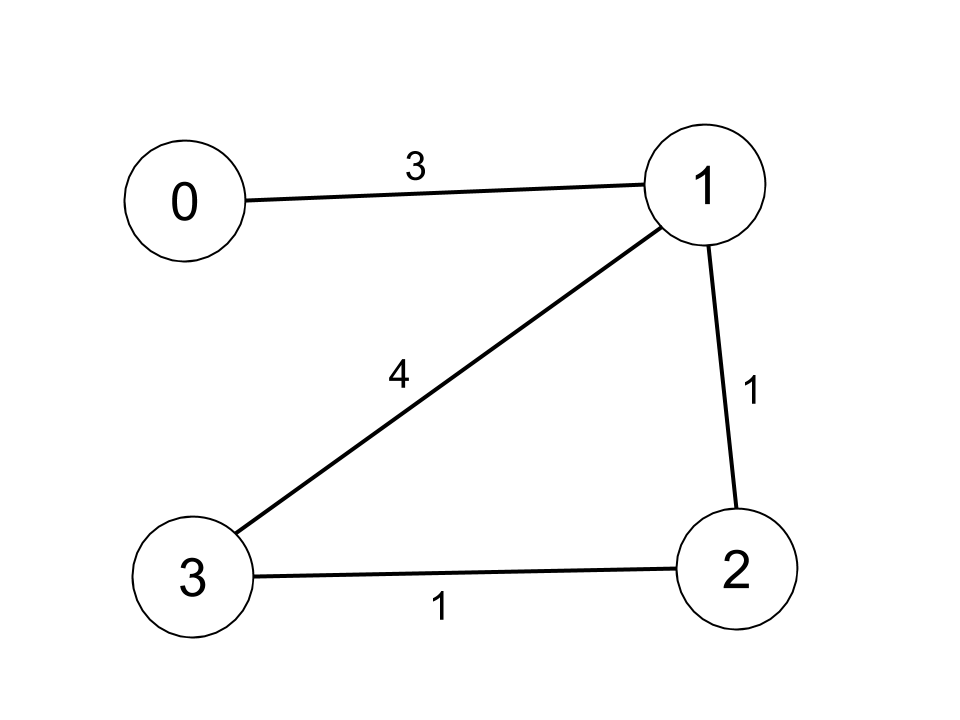+Input: n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
+Output: 3
+Explanation: The figure above describes the graph. 
+The neighboring cities at a distanceThreshold = 4 for each city are:
+City 0 -> [City 1, City 2] 
+City 1 -> [City 0, City 2, City 3] 
+City 2 -> [City 0, City 1, City 3] 
+City 3 -> [City 1, City 2] 
+Cities 0 and 3 have 2 neighboring cities at a distanceThreshold = 4, but we have to return city 3 since it has the greatest number.
+```
+
+Example 2:
+
+![](https://assets.leetcode.com/uploads/2020/01/16/find_the_city_02.png)
+
+```
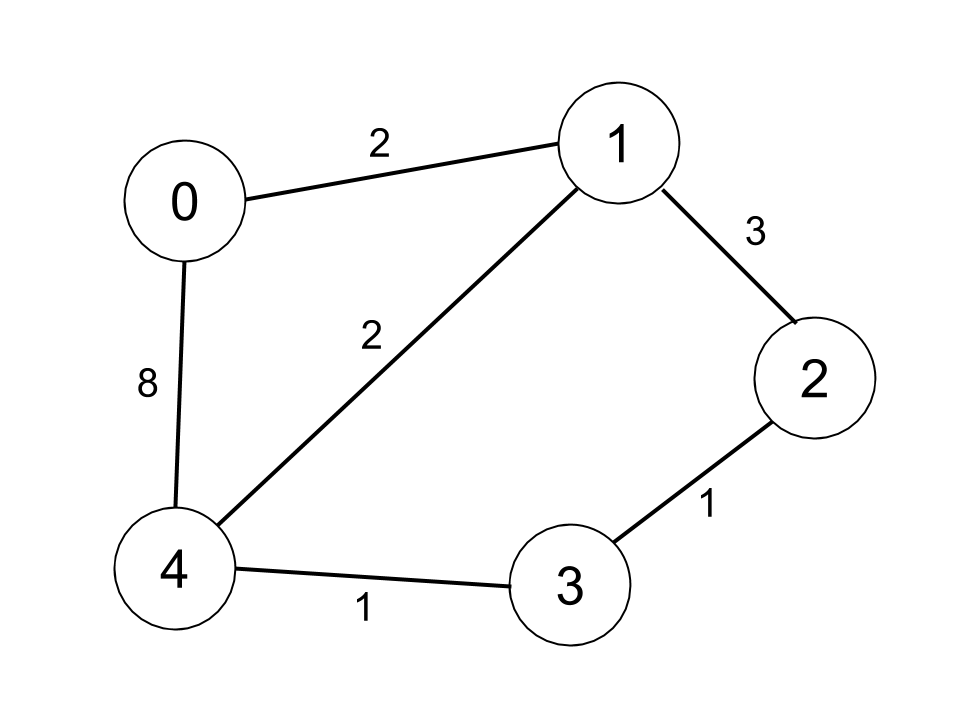+Input: n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
+Output: 0
+Explanation: The figure above describes the graph. 
+The neighboring cities at a distanceThreshold = 2 for each city are:
+City 0 -> [City 1] 
+City 1 -> [City 0, City 4] 
+City 2 -> [City 3, City 4] 
+City 3 -> [City 2, City 4]
+City 4 -> [City 1, City 2, City 3] 
+The city 0 has 1 neighboring city at a distanceThreshold = 2.
+```
+
+
+**Constraints:**
+
+
+
+- `2 <= n <= 100`
+
+- `1 <= edges.length <= n * (n - 1) / 2`
+
+- `edges[i].length == 3`
+
+- `0 <= fromi < toi < n`
+
+- `1 <= weighti, distanceThreshold <= 10^4`
+
+- All pairs `(fromi, toi)` are distinct.
+
+
+
+## Solution
+
+```javascript
+/**
+ * @param {number} n
+ * @param {number[][]} edges
+ * @param {number} distanceThreshold
+ * @return {number}
+ */
+var findTheCity = function(n, edges, distanceThreshold) {
+    var map = {};
+    for (var i = 0; i < edges.length; i++) {
+        map[edges[i][0]] = map[edges[i][0]] || {};
+        map[edges[i][1]] = map[edges[i][1]] || {};
+        map[edges[i][1]][edges[i][0]] = edges[i][2];
+        map[edges[i][0]][edges[i][1]] = edges[i][2];
+    }
+    var min = Number.MAX_SAFE_INTEGER;
+    var minNum = -1;
+    for (var j = 0; j < n; j++) {
+        var cities = dijkstra(j, map, distanceThreshold);
+        if (cities <= min) {
+            min = cities;
+            minNum = j;
+        }
+    }
+    return minNum;
+};
+
+var dijkstra = function(n, map, distanceThreshold) {
+    var visited = {};
+    var queue = new MinPriorityQueue();
+    queue.enqueue(n, 0);
+    while (queue.size() > 0) {
+        var { element, priority } = queue.dequeue();
+        if (priority > distanceThreshold) break;
+        if (visited[element]) continue;
+        visited[element] = true;
+        var arr = Object.keys(map[element] || {});
+        for (var i = 0; i < arr.length; i++) {
+            if (visited[arr[i]]) continue;
+            queue.enqueue(arr[i], priority + map[element][arr[i]]);
+        }
+    }
+    return Object.keys(visited).length;
+};
+```
+
+**Explain:**
+
+nope.
+
+**Complexity:**
+
+* Time complexity : O(n ^ 3 * log(n)).
+* Space complexity : O(n ^ 2).