feat: add 2058

2001-2100/2058. Find the Minimum and Maximum Number of Nodes Between Critical Points.md

@@ -0,0 +1,116 @@
+# 2058. Find the Minimum and Maximum Number of Nodes Between Critical Points
+
+- Difficulty: Medium.
+- Related Topics: Linked List.
+- Similar Questions: .
+
+## Problem
+
+A **critical point** in a linked list is defined as **either** a **local maxima** or a **local minima**.
+
+A node is a **local maxima** if the current node has a value **strictly greater** than the previous node and the next node.
+
+A node is a **local minima** if the current node has a value **strictly smaller** than the previous node and the next node.
+
+Note that a node can only be a local maxima/minima if there exists **both** a previous node and a next node.
+
+Given a linked list `head`, return **an array of length 2 containing **`[minDistance, maxDistance]`** where **`minDistance`** is the **minimum distance** between **any two distinct** critical points and **`maxDistance`** is the **maximum distance** between **any two distinct** critical points. If there are **fewer** than two critical points, return **`[-1, -1]`.
+
+
+Example 1:
+
+![](https://assets.leetcode.com/uploads/2021/10/13/a1.png)
+
+```
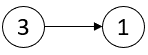+Input: head = [3,1]
+Output: [-1,-1]
+Explanation: There are no critical points in [3,1].
+```
+
+Example 2:
+
+![](https://assets.leetcode.com/uploads/2021/10/13/a2.png)
+
+```
+Input: head = [5,3,1,2,5,1,2]
+Output: [1,3]
+Explanation: There are three critical points:
+- [5,3,1,2,5,1,2]: The third node is a local minima because 1 is less than 3 and 2.
+- [5,3,1,2,5,1,2]: The fifth node is a local maxima because 5 is greater than 2 and 1.
+- [5,3,1,2,5,1,2]: The sixth node is a local minima because 1 is less than 5 and 2.
+The minimum distance is between the fifth and the sixth node. minDistance = 6 - 5 = 1.
+The maximum distance is between the third and the sixth node. maxDistance = 6 - 3 = 3.
+```
+
+Example 3:
+
+![](https://assets.leetcode.com/uploads/2021/10/14/a5.png)
+
+```
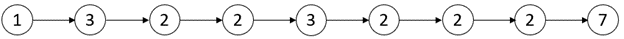+Input: head = [1,3,2,2,3,2,2,2,7]
+Output: [3,3]
+Explanation: There are two critical points:
+- [1,3,2,2,3,2,2,2,7]: The second node is a local maxima because 3 is greater than 1 and 2.
+- [1,3,2,2,3,2,2,2,7]: The fifth node is a local maxima because 3 is greater than 2 and 2.
+Both the minimum and maximum distances are between the second and the fifth node.
+Thus, minDistance and maxDistance is 5 - 2 = 3.
+Note that the last node is not considered a local maxima because it does not have a next node.
+```
+
+
+**Constraints:**
+
+
+
+- The number of nodes in the list is in the range `[2, 105]`.
+
+- `1 <= Node.val <= 105`
+
+
+
+## Solution
+
+```javascript
+/**
+ * Definition for singly-linked list.
+ * function ListNode(val, next) {
+ *     this.val = (val===undefined ? 0 : val)
+ *     this.next = (next===undefined ? null : next)
+ * }
+ */
+/**
+ * @param {ListNode} head
+ * @return {number[]}
+ */
+var nodesBetweenCriticalPoints = function(head) {
+    var firstPoint = -1;
+    var lastPoint = -1;
+    var last = null;
+    var now = head;
+    var i = 0;
+    var minDistance = Number.MAX_SAFE_INTEGER;
+    while (now) {
+        if (last && now.next && ((now.val > last.val && now.val > now.next.val) || (now.val < last.val && now.val < now.next.val))) {
+            if (firstPoint === -1) firstPoint = i;
+            if (lastPoint !== -1) minDistance = Math.min(minDistance, i - lastPoint);
+            lastPoint = i;
+        }
+        last = now;
+        now = now.next;
+        i += 1;
+    }
+    if (firstPoint !== -1 && lastPoint !== -1 && lastPoint !== firstPoint) {
+        return [minDistance, lastPoint - firstPoint];
+    }
+    return [-1, -1];
+};
+```
+
+**Explain:**
+
+nope.
+
+**Complexity:**
+
+* Time complexity : O(n).
+* Space complexity : O(n).