feat: solve No.2751

2701-2800/2751. Robot Collisions.md

@@ -0,0 +1,124 @@
+# 2751. Robot Collisions
+
+- Difficulty: Hard.
+- Related Topics: Array, Stack, Sorting, Simulation.
+- Similar Questions: Asteroid Collision.
+
+## Problem
+
+There are `n` **1-indexed** robots, each having a position on a line, health, and movement direction.
+
+You are given **0-indexed** integer arrays `positions`, `healths`, and a string `directions` (`directions[i]` is either **'L'** for **left** or **'R'** for **right**). All integers in `positions` are **unique**.
+
+All robots start moving on the line** simultaneously** at the **same speed **in their given directions. If two robots ever share the same position while moving, they will **collide**.
+
+If two robots collide, the robot with **lower health** is **removed** from the line, and the health of the other robot **decreases** **by one**. The surviving robot continues in the **same** direction it was going. If both robots have the **same** health, they are both** **removed from the line.
+
+Your task is to determine the **health** of the robots that survive the collisions, in the same **order **that the robots were given,** **i.e. final heath of robot 1 (if survived), final health of robot 2 (if survived), and so on. If there are no survivors, return an empty array.
+
+Return **an array containing the health of the remaining robots (in the order they were given in the input), after no further collisions can occur.**
+
+**Note:** The positions may be unsorted.
+
+
+
+
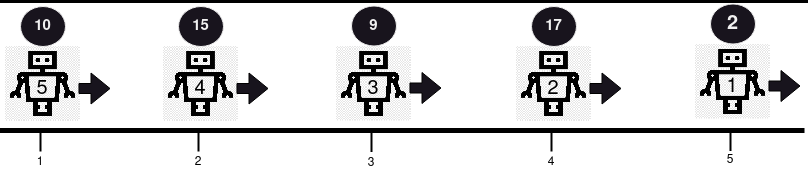
+Example 1:
+
+
+![](https://assets.leetcode.com/uploads/2023/05/15/image-20230516011718-12.png)
+
+
+```
+Input: positions = [5,4,3,2,1], healths = [2,17,9,15,10], directions = "RRRRR"
+Output: [2,17,9,15,10]
+Explanation: No collision occurs in this example, since all robots are moving in the same direction. So, the health of the robots in order from the first robot is returned, [2, 17, 9, 15, 10].
+```
+
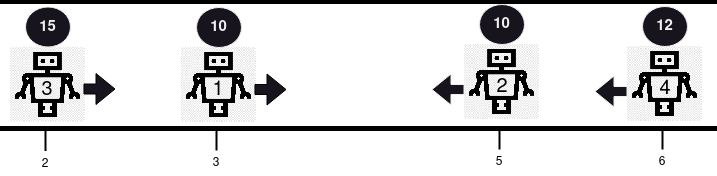
+Example 2:
+
+
+![](https://assets.leetcode.com/uploads/2023/05/15/image-20230516004433-7.png)
+
+
+```
+Input: positions = [3,5,2,6], healths = [10,10,15,12], directions = "RLRL"
+Output: [14]
+Explanation: There are 2 collisions in this example. Firstly, robot 1 and robot 2 will collide, and since both have the same health, they will be removed from the line. Next, robot 3 and robot 4 will collide and since robot 4's health is smaller, it gets removed, and robot 3's health becomes 15 - 1 = 14. Only robot 3 remains, so we return [14].
+```
+
+Example 3:
+
+
+![](https://assets.leetcode.com/uploads/2023/05/15/image-20230516005114-9.png)
+
+
+```
+Input: positions = [1,2,5,6], healths = [10,10,11,11], directions = "RLRL"
+Output: []
+Explanation: Robot 1 and robot 2 will collide and since both have the same health, they are both removed. Robot 3 and 4 will collide and since both have the same health, they are both removed. So, we return an empty array, [].
+```
+
+
+**Constraints:**
+
+
+
+- `1 <= positions.length == healths.length == directions.length == n <= 105`
+
+- `1 <= positions[i], healths[i] <= 109`
+
+- `directions[i] == 'L'` or `directions[i] == 'R'`
+
+- All values in `positions` are distinct
+
+
+
+## Solution
+
+```javascript
+/**
+ * @param {number[]} positions
+ * @param {number[]} healths
+ * @param {string} directions
+ * @return {number[]}
+ */
+var survivedRobotsHealths = function(positions, healths, directions) {
+    var res = [];
+    var stack = [];
+    var robots = positions.map((p, i) => [p, healths[i], directions[i], i]).sort((a, b) => a[0] - b[0]);
+    for (var i = 0; i < robots.length; i++) {
+        var robot = robots[i];
+        if (robot[2] === 'R') {
+            stack.push(robot);
+            continue;
+        }
+        while (robot[1] > 0 && stack.length) {
+            if (stack[stack.length - 1][1] < robot[1]) {
+                stack.pop();
+                robot[1] -= 1;
+            } else if (stack[stack.length - 1][1] === robot[1]) {
+                stack.pop();
+                robot[1] = 0;
+            } else {
+                stack[stack.length - 1][1] -= 1;
+                robot[1] = 0;
+            }
+        }
+        if (robot[1] > 0) {
+            res.push(robot);
+        }
+    }
+    res.push(...stack);
+    return res.sort((a, b) => a[3] - b[3]).map(a => a[1]);
+};
+```
+
+**Explain:**
+
+nope.
+
+**Complexity:**
+
+* Time complexity : O(n log(n)).
+* Space complexity : O(n).