-
Notifications
You must be signed in to change notification settings - Fork 75
Commit
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
decouple basis from storage type (#517)
* adding in explicit basis code * add polynomial_composition code path * fix bug in scalar_add * WIP: coeffs * WIP: doc adjustments * WIP: fiddle with promotion * WIP: identify DescriptorSystems issue * WIP: More promotions to match old behaviours * WIP: run doctests, adjust Chebyshev printing * WIP: convert * WIP: change Polynomial type; migrate standard-basis.jl * WIP: work to shift to new base type for most polys * doc fix=true * WIP: fixes for downstream * relax error type for nightly * add skip, not broken for a test * aqua test * WIP, update docs, reduce redundancies * WIP: more cleanup * don't test Aqua on 1.6 * clean up * test that copy is not alias * clean up identified invalidations * remove tests of deprecated (now removed) functions * reorg docs * fix sparse * * reorg docs * fix sparse * * SP test * WIP: more cleanup * version bump; signal breaking changes
- Loading branch information
Showing
49 changed files
with
3,676 additions
and
2,471 deletions.
There are no files selected for viewing
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
|
|
@@ -5,3 +5,4 @@ docs/site/ | |
| *.jl.mem | ||
|
|
||
| Manifest.toml | ||
| archive/ | ||
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -1,326 +1,8 @@ | ||
| # Polynomials.jl | ||
|
|
||
| Basic arithmetic, integration, differentiation, evaluation, and root finding over dense univariate [polynomials](https://en.wikipedia.org/wiki/Polynomial). | ||
| Basic arithmetic, integration, differentiation, evaluation, root finding, and fitting for | ||
| univariate [polynomials](https://en.wikipedia.org/wiki/Polynomial) in [Julia](https://julialang.org/). | ||
|
|
||
| [](https://JuliaMath.github.io/Polynomials.jl/stable) | ||
| [](https://github.com/JuliaMath/Polynomials.jl/actions/workflows/ci.yml) | ||
| [](https://codecov.io/gh/JuliaMath/Polynomials.jl) | ||
|
|
||
|
|
||
| ## Installation | ||
|
|
||
| ```julia | ||
| (v1.6) pkg> add Polynomials | ||
| ``` | ||
|
|
||
| This package supports Julia v1.6 and later. | ||
|
|
||
| ## Available Types of Polynomials | ||
|
|
||
| * `Polynomial` – standard basis polynomials, $a(x) = a_0 + a_1 x + a_2 x^2 + … + a_n x^n$ for $n ≥ 0$. | ||
| * `ImmutablePolynomial` – standard basis polynomials backed by a [Tuple type](https://docs.julialang.org/en/v1/manual/functions/#Tuples-1) for faster evaluation of values | ||
| * `SparsePolynomial` – standard basis polynomial backed by a [dictionary](https://docs.julialang.org/en/v1/base/collections/#Dictionaries-1) to hold sparse high-degree polynomials | ||
| * `LaurentPolynomial` – [Laurent polynomials](https://docs.julialang.org/en/v1/base/collections/#Dictionaries-1), $a(x) = a_m x^m + … + a_n x^n$ for $m ≤ n$ and $m,n ∈ ℤ$. This is backed by an [offset array](https://github.com/JuliaArrays/OffsetArrays.jl); for example, if $m<0$ and $n>0$, we obtain $a(x) = a_m x^m + … + a_{-1} x^{-1} + a_0 + a_1 x + … + a_n x^n$ | ||
| * `FactoredPolynomial` – standard basis polynomials, storing the roots, with multiplicity, and leading coefficient of a polynomial | ||
| * `ChebyshevT` – [Chebyshev polynomials](https://en.wikipedia.org/wiki/Chebyshev_polynomials) of the first kind | ||
| * `RationalFunction` - a type for ratios of polynomials. | ||
|
|
||
| ## Usage | ||
|
|
||
| ```julia | ||
| julia> using Polynomials | ||
| ``` | ||
|
|
||
| ### Construction and Evaluation | ||
|
|
||
| Construct a polynomial from an array (a vector) of its coefficients, lowest order first. | ||
|
|
||
| ```julia | ||
| julia> Polynomial([1,0,3,4]) | ||
| Polynomial(1 + 3*x^2 + 4*x^3) | ||
| ``` | ||
|
|
||
| Optionally, the variable of the polynomial can be specified. | ||
|
|
||
| ```julia | ||
| julia> Polynomial([1,2,3], :s) | ||
| Polynomial(1 + 2*s + 3*s^2) | ||
| ``` | ||
|
|
||
| Construct a polynomial from its roots. | ||
|
|
||
| ```julia | ||
| julia> fromroots([1,2,3]) # (x-1)*(x-2)*(x-3) | ||
| Polynomial(-6 + 11*x - 6*x^2 + x^3) | ||
| ``` | ||
|
|
||
| Evaluate the polynomial `p` at `x`. | ||
|
|
||
| ```julia | ||
| julia> p = Polynomial([1, 0, -1]); | ||
| julia> p(0.1) | ||
| 0.99 | ||
| ``` | ||
|
|
||
| ### Arithmetic | ||
|
|
||
| Methods are added to the usual arithmetic operators so that they work on polynomials, and combinations of polynomials and scalars. | ||
|
|
||
| ```julia | ||
| julia> p = Polynomial([1,2]) | ||
| Polynomial(1 + 2*x) | ||
|
|
||
| julia> q = Polynomial([1, 0, -1]) | ||
| Polynomial(1 - x^2) | ||
|
|
||
| julia> p - q | ||
| Polynomial(2*x + x^2) | ||
|
|
||
| julia> p = Polynomial([1,2]) | ||
| Polynomial(1 + 2*x) | ||
|
|
||
| julia> q = Polynomial([1, 0, -1]) | ||
| Polynomial(1 - x^2) | ||
|
|
||
| julia> 2p | ||
| Polynomial(2 + 4*x) | ||
|
|
||
| julia> 2+p | ||
| Polynomial(3 + 2*x) | ||
|
|
||
| julia> p - q | ||
| Polynomial(2*x + x^2) | ||
|
|
||
| julia> p * q | ||
| Polynomial(1 + 2*x - x^2 - 2*x^3) | ||
|
|
||
| julia> q / 2 | ||
| Polynomial(0.5 - 0.5*x^2) | ||
|
|
||
| julia> q ÷ p # `div`, also `rem` and `divrem` | ||
| Polynomial(0.25 - 0.5*x) | ||
| ``` | ||
|
|
||
| Most operations involving polynomials with different variables will error. | ||
|
|
||
| ```julia | ||
| julia> p = Polynomial([1, 2, 3], :x); | ||
| julia> q = Polynomial([1, 2, 3], :s); | ||
| julia> p + q | ||
| ERROR: ArgumentError: Polynomials have different indeterminates | ||
| ``` | ||
|
|
||
| #### Construction and Evaluation | ||
|
|
||
| While polynomials of type `Polynomial` are mutable objects, operations such as | ||
| `+`, `-`, `*`, always create new polynomials without modifying its arguments. | ||
| The time needed for these allocations and copies of the polynomial coefficients | ||
| may be noticeable in some use cases. This is amplified when the coefficients | ||
| are for instance `BigInt` or `BigFloat` which are mutable themselves. | ||
| This can be avoided by modifying existing polynomials to contain the result | ||
| of the operation using the [MutableArithmetics (MA) API](https://github.com/jump-dev/MutableArithmetics.jl). | ||
|
|
||
| Consider for instance the following arrays of polynomials | ||
| ```julia | ||
| using Polynomials | ||
| d, m, n = 30, 20, 20 | ||
| p(d) = Polynomial(big.(1:d)) | ||
| A = [p(d) for i in 1:m, j in 1:n] | ||
| b = [p(d) for i in 1:n] | ||
| ``` | ||
|
|
||
| In this case, the arrays are mutable objects for which the elements are mutable | ||
| polynomials which have mutable coefficients (`BigInt`s). | ||
| These three nested levels of mutable objects communicate with the MA | ||
| API in order to reduce allocation. | ||
| Calling `A * b` requires approximately 40 MiB due to 2 M allocations | ||
| as it does not exploit any mutability. | ||
|
|
||
| Using | ||
|
|
||
| ```julia | ||
| using PolynomialsMutableArithmetics | ||
| ``` | ||
|
|
||
| to register `Polynomials` with `MutableArithmetics`, then multiplying with: | ||
|
|
||
| ```julia | ||
| using MutableArithmetics | ||
| const MA = MutableArithmetics | ||
| MA.operate(*, A, b) | ||
| ``` | ||
|
|
||
| exploits the mutability and hence only allocates approximately 70 KiB due to 4 k | ||
| allocations. | ||
|
|
||
| If the resulting vector is already allocated, e.g., | ||
|
|
||
| ```julia | ||
| z(d) = Polynomial([zero(BigInt) for i in 1:d]) | ||
| c = [z(2d - 1) for i in 1:m] | ||
| ``` | ||
|
|
||
| then we can exploit its mutability with | ||
|
|
||
| ```julia | ||
| MA.operate!(MA.add_mul, c, A, b) | ||
| ``` | ||
|
|
||
| to reduce the allocation down to 48 bytes due to 3 allocations. | ||
|
|
||
| These remaining allocations are due to the `BigInt` buffer used to | ||
| store the result of intermediate multiplications. This buffer can be | ||
| preallocated with: | ||
|
|
||
| ```julia | ||
| buffer = MA.buffer_for(MA.add_mul, typeof(c), typeof(A), typeof(b)) | ||
| MA.buffered_operate!(buffer, MA.add_mul, c, A, b) | ||
| ``` | ||
|
|
||
| then the second line is allocation-free. | ||
|
|
||
| The `MA.@rewrite` macro rewrite an expression into an equivalent code that | ||
| exploit the mutability of the intermediate results. | ||
| For instance | ||
| ```julia | ||
| MA.@rewrite(A1 * b1 + A2 * b2) | ||
| ``` | ||
| is rewritten into | ||
| ```julia | ||
| c = MA.operate!(MA.add_mul, MA.Zero(), A1, b1) | ||
| MA.operate!(MA.add_mul, c, A2, b2) | ||
| ``` | ||
| which is equivalent to | ||
| ```julia | ||
| c = MA.operate(*, A1, b1) | ||
| MA.mutable_operate!(MA.add_mul, c, A2, b2) | ||
| ``` | ||
|
|
||
| *Note that currently, only the `Polynomial` type implements the API and it only | ||
| implements part of it.* | ||
|
|
||
| ### Integrals and Derivatives | ||
|
|
||
| Integrate the polynomial `p` term by term, optionally adding a constant | ||
| term `k`. The degree of the resulting polynomial is one higher than the | ||
| degree of `p` (for a nonzero polynomial). | ||
|
|
||
| ```julia | ||
| julia> integrate(Polynomial([1, 0, -1])) | ||
| Polynomial(1.0*x - 0.3333333333333333*x^3) | ||
|
|
||
| julia> integrate(Polynomial([1, 0, -1]), 2) | ||
| Polynomial(2.0 + 1.0*x - 0.3333333333333333*x^3) | ||
| ``` | ||
|
|
||
| Differentiate the polynomial `p` term by term. For non-zero | ||
| polynomials the degree of the resulting polynomial is one lower than | ||
| the degree of `p`. | ||
|
|
||
| ```julia | ||
| julia> derivative(Polynomial([1, 3, -1])) | ||
| Polynomial(3 - 2*x) | ||
| ``` | ||
|
|
||
| ### Root-finding | ||
|
|
||
|
|
||
| Return the roots (zeros) of `p`, with multiplicity. The number of | ||
| roots returned is equal to the degree of `p`. By design, this is not type-stable, the returned roots may be real or complex. | ||
|
|
||
| ```julia | ||
| julia> roots(Polynomial([1, 0, -1])) | ||
| 2-element Vector{Float64}: | ||
| -1.0 | ||
| 1.0 | ||
|
|
||
| julia> roots(Polynomial([1, 0, 1])) | ||
| 2-element Vector{ComplexF64}: | ||
| 0.0 - 1.0im | ||
| 0.0 + 1.0im | ||
|
|
||
| julia> roots(Polynomial([0, 0, 1])) | ||
| 2-element Vector{Float64}: | ||
| 0.0 | ||
| 0.0 | ||
| ``` | ||
|
|
||
| ### Fitting arbitrary data | ||
|
|
||
| Fit a polynomial (of degree `deg` or less) to `x` and `y` using a least-squares approximation. | ||
|
|
||
| ```julia | ||
| julia> xs = 0:4; ys = @. exp(-xs) + sin(xs); | ||
|
|
||
| julia> fit(xs, ys) |> p -> round.(coeffs(p), digits=4) |> Polynomial | ||
| Polynomial(1.0 + 0.0593*x + 0.3959*x^2 - 0.2846*x^3 + 0.0387*x^4) | ||
|
|
||
| julia> fit(ChebyshevT, xs, ys, 2) |> p -> round.(coeffs(p), digits=4) |> ChebyshevT | ||
| ChebyshevT(0.5413⋅T_0(x) - 0.8991⋅T_1(x) - 0.4238⋅T_2(x)) | ||
| ``` | ||
|
|
||
| Visual example: | ||
|
|
||
| 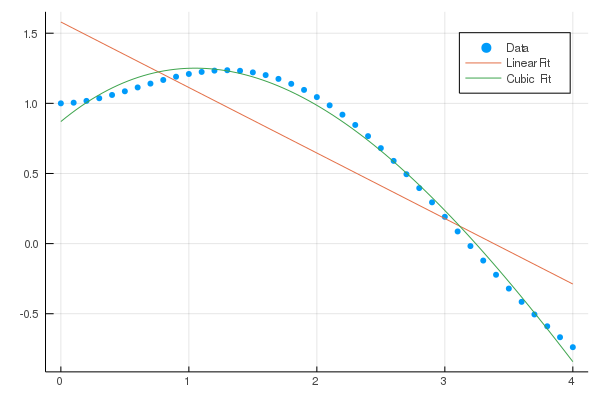 | ||
|
|
||
| ### Other methods | ||
|
|
||
| Polynomial objects also have other methods: | ||
|
|
||
| * For standard basis polynomials, 0-based indexing is used to extract | ||
| the coefficients of `[a0, a1, a2, ...]`; for mutable polynomials, | ||
| coefficients may be changed using indexing notation. | ||
|
|
||
| * `coeffs`: returns the coefficients | ||
|
|
||
| * `degree`: returns the polynomial degree, `length` is number of stored coefficients | ||
|
|
||
| * `variable`: returns the polynomial symbol as a polynomial in the underlying type | ||
|
|
||
| * `LinearAlgebra.norm`: find the `p`-norm of a polynomial | ||
|
|
||
| * `conj`: finds the conjugate of a polynomial over a complex field | ||
|
|
||
| * `truncate`: set to 0 all small terms in a polynomial; | ||
|
|
||
| * `chop` chops off any small leading values that may arise due to floating point operations. | ||
|
|
||
| * `gcd`: greatest common divisor of two polynomials. | ||
|
|
||
| * `Pade`: Return the | ||
| [Padé approximant](https://en.wikipedia.org/wiki/Pad%C3%A9_approximant) of order `m/n` for a polynomial as a `Pade` object. | ||
|
|
||
|
|
||
| ## Related Packages | ||
|
|
||
| * [StaticUnivariatePolynomials.jl](https://github.com/tkoolen/StaticUnivariatePolynomials.jl) Fixed-size univariate polynomials backed by a Tuple | ||
|
|
||
| * [MultiPoly.jl](https://github.com/daviddelaat/MultiPoly.jl) for sparse multivariate polynomials | ||
|
|
||
| * [DynamicPolynomials.jl](https://github.com/JuliaAlgebra/DynamicPolynomials.jl) Multivariate polynomials implementation of commutative and non-commutative variables | ||
|
|
||
| * [MultivariatePolynomials.jl](https://github.com/JuliaAlgebra/MultivariatePolynomials.jl) for multivariate polynomials and moments of commutative or non-commutative variables | ||
|
|
||
| * [PolynomialRings.jl](https://github.com/tkluck/PolynomialRings.jl) A library for arithmetic and algebra with multi-variable polynomials. | ||
|
|
||
| * [AbstractAlgebra.jl](https://github.com/wbhart/AbstractAlgebra.jl), [Nemo.jl](https://github.com/wbhart/Nemo.jl) for generic polynomial rings, matrix spaces, fraction fields, residue rings, power series, [Hecke.jl](https://github.com/thofma/Hecke.jl) for algebraic number theory. | ||
|
|
||
| * [LaurentPolynomials.jl](https://github.com/jmichel7/LaurentPolynomials.jl) A package for Laurent polynomials. | ||
|
|
||
| * [CommutativeAlgebra.jl](https://github.com/KlausC/CommutativeRings.jl) the start of a computer algebra system specialized to discrete calculations with support for polynomials. | ||
|
|
||
| * [PolynomialRoots.jl](https://github.com/giordano/PolynomialRoots.jl) for a fast complex polynomial root finder. For larger degree problems, also [FastPolynomialRoots](https://github.com/andreasnoack/FastPolynomialRoots.jl) and [AMRVW](https://github.com/jverzani/AMRVW.jl). For real roots only [RealPolynomialRoots](https://github.com/jverzani/RealPolynomialRoots.jl). | ||
|
|
||
|
|
||
| * [SpecialPolynomials.jl](https://github.com/jverzani/SpecialPolynomials.jl) A package providing various polynomial types beyond the standard basis polynomials in `Polynomials.jl`. Includes interpolating polynomials, Bernstein polynomials, and classical orthogonal polynomials. | ||
|
|
||
| * [ClassicalOrthogonalPolynomials.jl](https://github.com/JuliaApproximation/ClassicalOrthogonalPolynomials.jl) A Julia package for classical orthogonal polynomials and expansions. Includes `chebyshevt`, `chebyshevu`, `legendrep`, `jacobip`, `ultrasphericalc`, `hermiteh`, and `laguerrel`. The same repository includes `FastGaussQuadrature.jl`, `FastTransforms.jl`, and the `ApproxFun` packages. | ||
|
|
||
|
|
||
| ## Legacy code | ||
|
|
||
| As of v0.7, the internals of this package were greatly generalized and new types and method names were introduced. For compatibility purposes, legacy code can be run after issuing `using Polynomials.PolyCompat`. | ||
|
|
||
| ## Contributing | ||
|
|
||
| If you are interested in contributing, feel free to open an issue or pull request to get started. |
Oops, something went wrong.
27d548fThere was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
@JuliaRegistrator register
27d548fThere was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Registration pull request created: JuliaRegistries/General/89704
After the above pull request is merged, it is recommended that a tag is created on this repository for the registered package version.
This will be done automatically if the Julia TagBot GitHub Action is installed, or can be done manually through the github interface, or via: