| comments | difficulty | edit_url | rating | source | tags | ||
|---|---|---|---|---|---|---|---|
true |
简单 |
1280 |
第 34 场双周赛 Q1 |
|
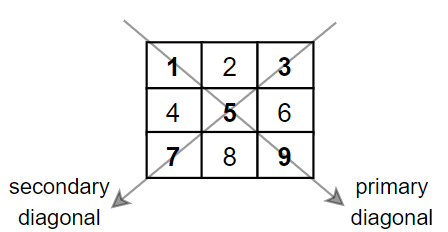
给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。
请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。
示例 1:
输入:mat = [[1,2,3], [4,5,6], [7,8,9]] 输出:25 解释:对角线的和为:1 + 5 + 9 + 3 + 7 = 25 请注意,元素 mat[1][1] = 5 只会被计算一次。
示例 2:
输入:mat = [[1,1,1,1], [1,1,1,1], [1,1,1,1], [1,1,1,1]] 输出:8
示例 3:
输入:mat = [[5]] 输出:5
提示:
n == mat.length == mat[i].length1 <= n <= 1001 <= mat[i][j] <= 100
我们可以遍历矩阵的每一行
遍历完所有行后,即可得到答案。
时间复杂度
class Solution:
def diagonalSum(self, mat: List[List[int]]) -> int:
ans = 0
n = len(mat)
for i, row in enumerate(mat):
j = n - i - 1
ans += row[i] + (0 if j == i else row[j])
return ansclass Solution {
public int diagonalSum(int[][] mat) {
int ans = 0;
int n = mat.length;
for (int i = 0; i < n; ++i) {
int j = n - i - 1;
ans += mat[i][i] + (i == j ? 0 : mat[i][j]);
}
return ans;
}
}class Solution {
public:
int diagonalSum(vector<vector<int>>& mat) {
int ans = 0;
int n = mat.size();
for (int i = 0; i < n; ++i) {
int j = n - i - 1;
ans += mat[i][i] + (i == j ? 0 : mat[i][j]);
}
return ans;
}
};func diagonalSum(mat [][]int) (ans int) {
n := len(mat)
for i, row := range mat {
ans += row[i]
if j := n - i - 1; j != i {
ans += row[j]
}
}
return
}function diagonalSum(mat: number[][]): number {
let ans = 0;
const n = mat.length;
for (let i = 0; i < n; ++i) {
const j = n - i - 1;
ans += mat[i][i] + (i === j ? 0 : mat[i][j]);
}
return ans;
}impl Solution {
pub fn diagonal_sum(mat: Vec<Vec<i32>>) -> i32 {
let n = mat.len();
let mut ans = 0;
for i in 0..n {
ans += mat[i][i] + mat[n - 1 - i][i];
}
if (n & 1) == 1 {
ans -= mat[n >> 1][n >> 1];
}
ans
}
}int diagonalSum(int** mat, int matSize, int* matColSize) {
int ans = 0;
for (int i = 0; i < matSize; i++) {
ans += mat[i][i] + mat[i][matSize - 1 - i];
}
if (matSize & 1) {
ans -= mat[matSize >> 1][matSize >> 1];
}
return ans;
}function diagonalSum(mat: number[][]): number {
const n = mat.length;
let ans = 0;
for (let i = 0; i < n; i++) {
ans += mat[i][i] + mat[i][n - 1 - i];
}
if (n & 1) {
ans -= mat[n >> 1][n >> 1];
}
return ans;
}