comments

difficulty

edit_url

rating

source

3240. 最少翻转次数使二进制矩阵回文 II

English Version

题目描述

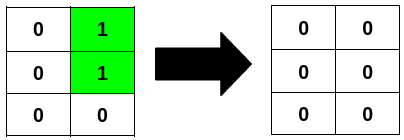
给你一个 m x n 的二进制矩阵 grid 。

如果矩阵中一行或者一列从前往后与从后往前读是一样的，那么我们称这一行或者这一列是回文的。

你可以将 grid 中任意格子的值翻转，也就是将格子里的值从 0 变成 1 ，或者从 1 变成 0 。

请你返回最少翻转次数，使得矩阵中所有行和列都是 回文的 ，且矩阵中 1 的数目可以被 4 整除。

示例 1：

输入：grid = [[1,0,0],[0,1,0],[0,0,1]]

输出：3

解释：

示例 2：

输入：grid = [[0,1],[0,1],[0,0]]

输出：2

解释：

示例 3：

输入：grid = [[1],[1]]

输出：2

解释：

提示：

m == grid.length
n == grid[i].length
1 <= m * n <= 2 * 10⁵
0 <= grid[i][j] <= 1

解法

方法一：分类讨论

行和列都是回文的，那么对于任意 $i \in [0, m / 2)$ 和 $j \in [0, n / 2)$，都需要满足 $\text{grid}[i][j] = \text{grid}[m - i - 1][j] = \text{grid}[i][n - j - 1] = \text{grid}[m - i - 1][n - j - 1]$，要么都变成 $0$，要么都变成 $1$，变成 $0$ 的次数为 $c_0 = \text{grid}[i][j] + \text{grid}[m - i - 1][j] + \text{grid}[i][n - j - 1] + \text{grid}[m - i - 1][n - j - 1]$，变成 $1$ 的次数为 $c_1 = 4 - c_0$，取两者的较小值，累加到答案中。

接下来，我们再讨论 $m$ 和 $n$ 的奇偶性：

如果 $m$ 和 $n$ 都是偶数，那么直接返回答案；
如果 $m$ 和 $n$ 都是奇数，那么最中间的格子只能是 $0$，因为题目要求 $1$ 的数目可以被 $4$ 整除；
如果 $m$ 是奇数，而 $n$ 是偶数，那么我们需要考虑最中间的一行；
如果 $m$ 是偶数，而 $n$ 是奇数，那么我们需要考虑最中间的一列。

对于后两种情况，我们需要统计最中间的一行或一列中对应位置不相同的格子对数 $\text{diff}$，以及对应位置相同且为 $1$ 的格子个数 $\text{cnt1}$，然后再分情况讨论：

如果 $\text{cnt1} \bmod 4 = 0$，那么我们只需要将 $\text{diff}$ 个格子变成 $0$ 即可，操作次数为 $\text{diff}$；
否则，说明 $\text{cnt1} = 2$，此时如果 $\text{diff} \lt 0$，我们可以将其中一个格子变成 $1$，使得 $\text{cnt1} = 4$，那么剩下的 $\text{diff} - 1$ 个格子变成 $0$ 即可，操作次数一共为 $\text{diff}$。
否则，如果 $\text{diff} = 0$，我们就把 $\text{2}$ 个格子变成 $0$，使得 $\text{cnt1} \bmod 4 = 0$，操作次数为 $\text{2}$。

我们将操作次数累加到答案中，最后返回答案即可。

时间复杂度 $O(m \times n)$，其中 $m$ 和 $n$ 分别是矩阵的行数和列数。空间复杂度 $O(1)$。

Python3

class Solution:
    def minFlips(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        ans = 0
        for i in range(m // 2):
            for j in range(n // 2):
                x, y = m - i - 1, n - j - 1
                cnt1 = grid[i][j] + grid[x][j] + grid[i][y] + grid[x][y]
                ans += min(cnt1, 4 - cnt1)
        if m % 2 and n % 2:
            ans += grid[m // 2][n // 2]
        diff = cnt1 = 0
        if m % 2:
            for j in range(n // 2):
                if grid[m // 2][j] == grid[m // 2][n - j - 1]:
                    cnt1 += grid[m // 2][j] * 2
                else:
                    diff += 1
        if n % 2:
            for i in range(m // 2):
                if grid[i][n // 2] == grid[m - i - 1][n // 2]:
                    cnt1 += grid[i][n // 2] * 2
                else:
                    diff += 1
        ans += diff if cnt1 % 4 == 0 or diff else 2
        return ans

Java

class Solution {
    public int minFlips(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        int ans = 0;
        for (int i = 0; i < m / 2; ++i) {
            for (int j = 0; j < n / 2; ++j) {
                int x = m - i - 1, y = n - j - 1;
                int cnt1 = grid[i][j] + grid[x][j] + grid[i][y] + grid[x][y];
                ans += Math.min(cnt1, 4 - cnt1);
            }
        }
        if (m % 2 == 1 && n % 2 == 1) {
            ans += grid[m / 2][n / 2];
        }

        int diff = 0, cnt1 = 0;
        if (m % 2 == 1) {
            for (int j = 0; j < n / 2; ++j) {
                if (grid[m / 2][j] == grid[m / 2][n - j - 1]) {
                    cnt1 += grid[m / 2][j] * 2;
                } else {
                    diff += 1;
                }
            }
        }
        if (n % 2 == 1) {
            for (int i = 0; i < m / 2; ++i) {
                if (grid[i][n / 2] == grid[m - i - 1][n / 2]) {
                    cnt1 += grid[i][n / 2] * 2;
                } else {
                    diff += 1;
                }
            }
        }
        ans += cnt1 % 4 == 0 || diff > 0 ? diff : 2;
        return ans;
    }
}

C++

class Solution {
public:
    int minFlips(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        int ans = 0;
        for (int i = 0; i < m / 2; ++i) {
            for (int j = 0; j < n / 2; ++j) {
                int x = m - i - 1, y = n - j - 1;
                int cnt1 = grid[i][j] + grid[x][j] + grid[i][y] + grid[x][y];
                ans += min(cnt1, 4 - cnt1);
            }
        }
        if (m % 2 == 1 && n % 2 == 1) {
            ans += grid[m / 2][n / 2];
        }

        int diff = 0, cnt1 = 0;
        if (m % 2 == 1) {
            for (int j = 0; j < n / 2; ++j) {
                if (grid[m / 2][j] == grid[m / 2][n - j - 1]) {
                    cnt1 += grid[m / 2][j] * 2;
                } else {
                    diff += 1;
                }
            }
        }
        if (n % 2 == 1) {
            for (int i = 0; i < m / 2; ++i) {
                if (grid[i][n / 2] == grid[m - i - 1][n / 2]) {
                    cnt1 += grid[i][n / 2] * 2;
                } else {
                    diff += 1;
                }
            }
        }
        ans += cnt1 % 4 == 0 || diff > 0 ? diff : 2;
        return ans;
    }
};

Go

func minFlips(grid [][]int) int {
	m, n := len(grid), len(grid[0])
	ans := 0

	for i := 0; i < m/2; i++ {
		for j := 0; j < n/2; j++ {
			x, y := m-i-1, n-j-1
			cnt1 := grid[i][j] + grid[x][j] + grid[i][y] + grid[x][y]
			ans += min(cnt1, 4-cnt1)
		}
	}

	if m%2 == 1 && n%2 == 1 {
		ans += grid[m/2][n/2]
	}

	diff, cnt1 := 0, 0

	if m%2 == 1 {
		for j := 0; j < n/2; j++ {
			if grid[m/2][j] == grid[m/2][n-j-1] {
				cnt1 += grid[m/2][j] * 2
			} else {
				diff += 1
			}
		}
	}

	if n%2 == 1 {
		for i := 0; i < m/2; i++ {
			if grid[i][n/2] == grid[m-i-1][n/2] {
				cnt1 += grid[i][n/2] * 2
			} else {
				diff += 1
			}
		}
	}

	if cnt1%4 == 0 || diff > 0 {
		ans += diff
	} else {
		ans += 2
	}

	return ans
}

TypeScript

function minFlips(grid: number[][]): number {
    const m = grid.length;
    const n = grid[0].length;
    let ans = 0;

    for (let i = 0; i < Math.floor(m / 2); i++) {
        for (let j = 0; j < Math.floor(n / 2); j++) {
            const x = m - i - 1;
            const y = n - j - 1;
            const cnt1 = grid[i][j] + grid[x][j] + grid[i][y] + grid[x][y];
            ans += Math.min(cnt1, 4 - cnt1);
        }
    }

    if (m % 2 === 1 && n % 2 === 1) {
        ans += grid[Math.floor(m / 2)][Math.floor(n / 2)];
    }

    let diff = 0,
        cnt1 = 0;

    if (m % 2 === 1) {
        for (let j = 0; j < Math.floor(n / 2); j++) {
            if (grid[Math.floor(m / 2)][j] === grid[Math.floor(m / 2)][n - j - 1]) {
                cnt1 += grid[Math.floor(m / 2)][j] * 2;
            } else {
                diff += 1;
            }
        }
    }

    if (n % 2 === 1) {
        for (let i = 0; i < Math.floor(m / 2); i++) {
            if (grid[i][Math.floor(n / 2)] === grid[m - i - 1][Math.floor(n / 2)]) {
                cnt1 += grid[i][Math.floor(n / 2)] * 2;
            } else {
                diff += 1;
            }
        }
    }

    ans += cnt1 % 4 === 0 || diff > 0 ? diff : 2;
    return ans;
}

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

README.md

README.md

3240. 最少翻转次数使二进制矩阵回文 II

题目描述

解法

方法一：分类讨论

Python3

Java

C++

Go

TypeScript

Files

README.md

Latest commit

History

README.md

File metadata and controls

3240. 最少翻转次数使二进制矩阵回文 II

题目描述

解法

方法一：分类讨论

Python3

Java

C++

Go

TypeScript