Skip to content

Latest commit

 

History

History
329 lines (263 loc) · 10.4 KB

README_EN.md

File metadata and controls

329 lines (263 loc) · 10.4 KB
comments difficulty edit_url rating source tags
true
Medium
2080
Biweekly Contest 136 Q3
Array
Two Pointers
Matrix

3240. Minimum Number of Flips to Make Binary Grid Palindromic II

中文文档

Description

You are given an m x n binary matrix grid.

A row or column is considered palindromic if its values read the same forward and backward.

You can flip any number of cells in grid from 0 to 1, or from 1 to 0.

Return the minimum number of cells that need to be flipped to make all rows and columns palindromic, and the total number of 1's in grid divisible by 4.

 

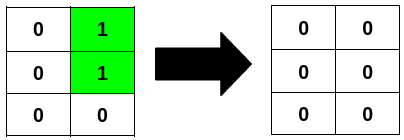
Example 1:

Input: grid = [[1,0,0],[0,1,0],[0,0,1]]

Output: 3

Explanation:

Example 2:

Input: grid = [[0,1],[0,1],[0,0]]

Output: 2

Explanation:

Example 3:

Input: grid = [[1],[1]]

Output: 2

Explanation:

 

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m * n <= 2 * 105
  • 0 <= grid[i][j] <= 1

Solutions

Solution 1: Case Analysis

If both rows and columns are palindromic, then for any $i \in [0, m / 2)$ and $j \in [0, n / 2)$, it must satisfy $\text{grid}[i][j] = \text{grid}[m - i - 1][j] = \text{grid}[i][n - j - 1] = \text{grid}[m - i - 1][n - j - 1]$. They must either all become $0$ or all become $1$. The number of changes to $0$ is $c_0 = \text{grid}[i][j] + \text{grid}[m - i - 1][j] + \text{grid}[i][n - j - 1] + \text{grid}[m - i - 1][n - j - 1]$, and the number of changes to $1$ is $c_1 = 4 - c_0$. We take the minimum of the two and add it to the answer.

Next, we discuss the parity of $m$ and $n$:

  • If both $m$ and $n$ are even, we directly return the answer.
  • If both $m$ and $n$ are odd, the center cell must be $0$ because the number of $1$s must be divisible by $4$.
  • If $m$ is odd and $n$ is even, we need to consider the middle row.
  • If $m$ is even and $n$ is odd, we need to consider the middle column.

For the latter two cases, we need to count the number of differing pairs of cells $\text{diff}$ in the middle row or column, and the number of cells that are the same and equal to $1$ $\text{cnt1}$. Then we discuss the following cases:

  • If $\text{cnt1} \bmod 4 = 0$, we only need to change the $\text{diff}$ cells to $0$, and the number of operations is $\text{diff}$.
  • Otherwise, if $\text{cnt1} = 2$, if $\text{diff} \lt 0$, we can change one of the cells to $1$ to make $\text{cnt1} = 4$, and then change the remaining $\text{diff} - 1$ cells to $0$. The total number of operations is $\text{diff}$.
  • Otherwise, if $\text{diff} = 0$, we change the $2$ cells to $0$ to make $\text{cnt1} \bmod 4 = 0$, and the number of operations is $2$.

We add the number of operations to the answer and finally return the answer.

The time complexity is $O(m \times n)$, where $m$ and $n$ are the number of rows and columns of the matrix, respectively. The space complexity is $O(1)$.

Python3

class Solution:
    def minFlips(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        ans = 0
        for i in range(m // 2):
            for j in range(n // 2):
                x, y = m - i - 1, n - j - 1
                cnt1 = grid[i][j] + grid[x][j] + grid[i][y] + grid[x][y]
                ans += min(cnt1, 4 - cnt1)
        if m % 2 and n % 2:
            ans += grid[m // 2][n // 2]
        diff = cnt1 = 0
        if m % 2:
            for j in range(n // 2):
                if grid[m // 2][j] == grid[m // 2][n - j - 1]:
                    cnt1 += grid[m // 2][j] * 2
                else:
                    diff += 1
        if n % 2:
            for i in range(m // 2):
                if grid[i][n // 2] == grid[m - i - 1][n // 2]:
                    cnt1 += grid[i][n // 2] * 2
                else:
                    diff += 1
        ans += diff if cnt1 % 4 == 0 or diff else 2
        return ans

Java

class Solution {
    public int minFlips(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        int ans = 0;
        for (int i = 0; i < m / 2; ++i) {
            for (int j = 0; j < n / 2; ++j) {
                int x = m - i - 1, y = n - j - 1;
                int cnt1 = grid[i][j] + grid[x][j] + grid[i][y] + grid[x][y];
                ans += Math.min(cnt1, 4 - cnt1);
            }
        }
        if (m % 2 == 1 && n % 2 == 1) {
            ans += grid[m / 2][n / 2];
        }

        int diff = 0, cnt1 = 0;
        if (m % 2 == 1) {
            for (int j = 0; j < n / 2; ++j) {
                if (grid[m / 2][j] == grid[m / 2][n - j - 1]) {
                    cnt1 += grid[m / 2][j] * 2;
                } else {
                    diff += 1;
                }
            }
        }
        if (n % 2 == 1) {
            for (int i = 0; i < m / 2; ++i) {
                if (grid[i][n / 2] == grid[m - i - 1][n / 2]) {
                    cnt1 += grid[i][n / 2] * 2;
                } else {
                    diff += 1;
                }
            }
        }
        ans += cnt1 % 4 == 0 || diff > 0 ? diff : 2;
        return ans;
    }
}

C++

class Solution {
public:
    int minFlips(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        int ans = 0;
        for (int i = 0; i < m / 2; ++i) {
            for (int j = 0; j < n / 2; ++j) {
                int x = m - i - 1, y = n - j - 1;
                int cnt1 = grid[i][j] + grid[x][j] + grid[i][y] + grid[x][y];
                ans += min(cnt1, 4 - cnt1);
            }
        }
        if (m % 2 == 1 && n % 2 == 1) {
            ans += grid[m / 2][n / 2];
        }

        int diff = 0, cnt1 = 0;
        if (m % 2 == 1) {
            for (int j = 0; j < n / 2; ++j) {
                if (grid[m / 2][j] == grid[m / 2][n - j - 1]) {
                    cnt1 += grid[m / 2][j] * 2;
                } else {
                    diff += 1;
                }
            }
        }
        if (n % 2 == 1) {
            for (int i = 0; i < m / 2; ++i) {
                if (grid[i][n / 2] == grid[m - i - 1][n / 2]) {
                    cnt1 += grid[i][n / 2] * 2;
                } else {
                    diff += 1;
                }
            }
        }
        ans += cnt1 % 4 == 0 || diff > 0 ? diff : 2;
        return ans;
    }
};

Go

func minFlips(grid [][]int) int {
	m, n := len(grid), len(grid[0])
	ans := 0

	for i := 0; i < m/2; i++ {
		for j := 0; j < n/2; j++ {
			x, y := m-i-1, n-j-1
			cnt1 := grid[i][j] + grid[x][j] + grid[i][y] + grid[x][y]
			ans += min(cnt1, 4-cnt1)
		}
	}

	if m%2 == 1 && n%2 == 1 {
		ans += grid[m/2][n/2]
	}

	diff, cnt1 := 0, 0

	if m%2 == 1 {
		for j := 0; j < n/2; j++ {
			if grid[m/2][j] == grid[m/2][n-j-1] {
				cnt1 += grid[m/2][j] * 2
			} else {
				diff += 1
			}
		}
	}

	if n%2 == 1 {
		for i := 0; i < m/2; i++ {
			if grid[i][n/2] == grid[m-i-1][n/2] {
				cnt1 += grid[i][n/2] * 2
			} else {
				diff += 1
			}
		}
	}

	if cnt1%4 == 0 || diff > 0 {
		ans += diff
	} else {
		ans += 2
	}

	return ans
}

TypeScript

function minFlips(grid: number[][]): number {
    const m = grid.length;
    const n = grid[0].length;
    let ans = 0;

    for (let i = 0; i < Math.floor(m / 2); i++) {
        for (let j = 0; j < Math.floor(n / 2); j++) {
            const x = m - i - 1;
            const y = n - j - 1;
            const cnt1 = grid[i][j] + grid[x][j] + grid[i][y] + grid[x][y];
            ans += Math.min(cnt1, 4 - cnt1);
        }
    }

    if (m % 2 === 1 && n % 2 === 1) {
        ans += grid[Math.floor(m / 2)][Math.floor(n / 2)];
    }

    let diff = 0,
        cnt1 = 0;

    if (m % 2 === 1) {
        for (let j = 0; j < Math.floor(n / 2); j++) {
            if (grid[Math.floor(m / 2)][j] === grid[Math.floor(m / 2)][n - j - 1]) {
                cnt1 += grid[Math.floor(m / 2)][j] * 2;
            } else {
                diff += 1;
            }
        }
    }

    if (n % 2 === 1) {
        for (let i = 0; i < Math.floor(m / 2); i++) {
            if (grid[i][Math.floor(n / 2)] === grid[m - i - 1][Math.floor(n / 2)]) {
                cnt1 += grid[i][Math.floor(n / 2)] * 2;
            } else {
                diff += 1;
            }
        }
    }

    ans += cnt1 % 4 === 0 || diff > 0 ? diff : 2;
    return ans;
}